GATE ME 2014 Set 3
GATE ME
1
A machine produces $$0, 1$$ or $$2$$ defective pieces in a day with associated probability of $${1 \over 6},{2 \over 3}$$ and $${1 \over 6}$$, respectively. Then mean value and the variance of the number of defective pieces produced by
2
Consider a $$3 \times 3$$ real symmetric matrix $$S$$ such that two of its eigen values are $$a \ne 0,$$ $$b\,\, \ne 0$$ with respective eigen vectors $$\left[ {\matrix{
{{x_1}} \cr
{{x_2}} \cr
{{x_3}} \cr
} } \right],\left[ {\matrix{
{{y_1}} \cr
{{y_2}} \cr
{{y_3}} \cr
} } \right].$$ If $$a\, \ne b$$ then $${x_1}{y_1} + {x_2}{y_2} + {x_3}{y_3}$$ equals
3
If a function is continuous at a point,
4
Divergence of the vector field $${x^2}z\widehat i + xy\widehat j - y{z^2}\widehat k\,\,$$ at $$(1, -1, 1)$$ is
5
A group consists of equal number of men and women. Of this group $$20$$% of the men and $$50$$% of the women are unemployed. If a person is selected at random from this group, the probability of the selected person being employed is
6
Consider two solutions $$\,x\left( t \right)\,\,\,\, = \,\,\,{x_1}\left( t \right)\,\,$$ and $$x\left( t \right)\,\,\,\, = \,\,\,{x_2}\left( t \right)\,\,$$ of the differential equation
$$\,\,{{{d^2}x\left( t \right)} \over {d{t^2}}} + x\left( t \right) = 0,t > 0,\,\,$$ such that
$$\,{x_1}\left( 0 \right) = 1,{\left. {{{d{x_1}\left( t \right)} \over {dt}}} \right|_{t = 0}} = 0,$$ $$\,\,\,\,{x_2}\left( 0 \right) = 0,{\left. {{{d{x_2}\left( t \right)} \over {dt}}} \right|_{t = 0}} = 1$$
$$\,\,{{{d^2}x\left( t \right)} \over {d{t^2}}} + x\left( t \right) = 0,t > 0,\,\,$$ such that
$$\,{x_1}\left( 0 \right) = 1,{\left. {{{d{x_1}\left( t \right)} \over {dt}}} \right|_{t = 0}} = 0,$$ $$\,\,\,\,{x_2}\left( 0 \right) = 0,{\left. {{{d{x_2}\left( t \right)} \over {dt}}} \right|_{t = 0}} = 1$$
The wronskian $$\,w\left( t \right) = \left| {{{\matrix{ {{x_1}\left( t \right)} \cr {d{x_1}\left( t \right)} \cr } } \over {dt}}} \right.\left. {{{\matrix{ {{x_2}\left( t \right)} \cr {d{x_2}\left( t \right)} \cr } } \over {dt}}} \right|$$ at $$\,\,t = \pi /2$$
7
The definite integral $$\,\int\limits_1^3 {{1 \over x}} dx\,\,$$ is evaluated using Trapezoidal rule with a step size of $$1.$$ The correct answer is
8
The real root of the equation $$5x-2cosx=0$$ (up to two decimal accuracy) is
9
An analytic function of a complex variable $$z = x + iy$$ is expressed as
$$f\left( z \right) = u\left( {x + y} \right) + iv\left( {x,y} \right),$$ where $$i = \sqrt { - 1} .$$ If $$u(x, y)=$$ $${x^3} - {y^2}$$
then expression for $$v(x,y)$$ in terms of $$x,y$$ and a general constant $$c$$ would be
$$f\left( z \right) = u\left( {x + y} \right) + iv\left( {x,y} \right),$$ where $$i = \sqrt { - 1} .$$ If $$u(x, y)=$$ $${x^3} - {y^2}$$
then expression for $$v(x,y)$$ in terms of $$x,y$$ and a general constant $$c$$ would be
10
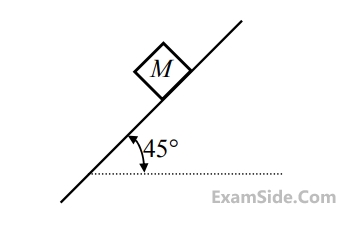
A body of mass (m) 10kg is initially stationary on a 45° inclined plane as shown in figure. The coefficient of dynamic friction between the body and the plane is 0.5. The body slides down the plane and attains a velocity of 20 m/s. The distance travelled (in meter) by the body along the plane is _______

11
An annular disc has a mass m, inner radius R and outer radius $$2R$$. The disc rolls on a flat surface without slipping. If the velocity of the center of mass is $$v,$$ the kinetic energy of the disc is
12
A four-wheel vehicle of mass 1000kg moves uniformly in a straight line with the wheels revolving at 10 rad/s. The wheel are identical, each with a radius of 0.2 m. Then a constant braking torque is applied to all the wheels and the vehicle experiences a uniform deceleration. For the vehicle to stop in 10s, the braking torque (in N. m) on each wheel is ___________.
13
A mass m1 of 100kg travelling with a uniform velocity of 5 m/s along a line collides with a stationary mass m2 of 1000kg. After the collision, both the masses travel together with the same velocity. The coefficient of restitution is
14
A fluid of dynamic viscosity $$2 \times {10^{ - 5}}\,\,kg/m.s$$ and density $$1kg/{m^3}$$ flows with an average velocity of
$$1$$ $$m/s$$ through a long duct of rectangular $$\left( {25\,\,mm \times \,\,15\,\,mm} \right)$$ cross-section. Assuming laminar flow, the pressure drop (in $$Pa$$) in the fully developed region per meter length of the duct is __________________.
15
Consider the turbulent flow of a fluid through a circular pipe of diameter, $$D.$$ Identify the correct pair of statements.
$${\rm I}.$$ The fluid is well-mixed
$${\rm II}.$$ The fluid is unmixed
$${\rm III}.$$ $$R{e_D} < 2300$$
$${\rm IV}.$$ $$R{e_D} > 2300$$
$${\rm I}.$$ The fluid is well-mixed
$${\rm II}.$$ The fluid is unmixed
$${\rm III}.$$ $$R{e_D} < 2300$$
$${\rm IV}.$$ $$R{e_D} > 2300$$
16
A siphon is used to drain water from a large tank as shown in the figure below. Assume that the level of water is maintained constant. Ignore frictional effect due to viscosity and losses at entry and exit. At the exit of the siphon, the velocity of water is

17
Consider a long cylindrical tube of inner and outer radii, $${r_i}$$ and $${r_0}$$ , respectively, length, $$L$$ and
thermal conductivity, $$k.$$ Its inner and outer surfaces are maintained at $${T_i}$$ and $${T_0}$$ , respectively
$$\left( {{T_i}\,\,\, > \,\,\,{T_0}} \right).$$ Assuming one-dimensional steady state heat conduction in the radial direction, the
thermal resistance in the wall of the tube is
18
Heat transfer through a composite wall is shown in figure. Both the sections of the wall have equal thickness $$\left( \ell \right)$$. The conductivity of one section is $$k$$ and that of the other is $$2k.$$ The left face of the wall is at $$600$$ $$K$$ and the right face is at $$300$$ $$K.$$
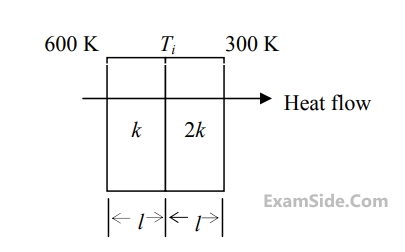

The interface temperature $${T_i}$$ (in $$K$$) of the composite wall is ___________
19
A solid sphere of radius$${r_1} = 20\,\,mm$$ is placed concentrically inside a hollow sphere of radius $${r_2} = 30\,\,mm$$ as shown in the figure.
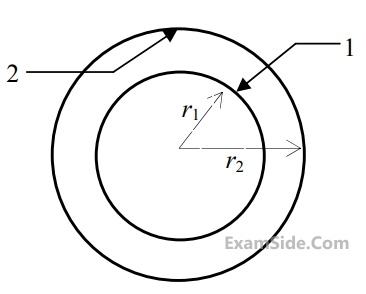

The view factor $${F_{21}}$$ for radiation heat transfer is
20
A double-pipe counter-flow heat exchanger transfers heat between two water streams. Tube side water at $$19$$ liter/s is heated from $${10^ \circ }C$$ to $${38^ \circ }C$$. Shell side water at $$25$$ liter/s is entering at $${46^ \circ }C$$. Assume constant properties of water; density is $$1000\,kg/{m^3}$$ and specific heat is $$4186$$ $$J/kg.K.$$ The $$LMTD$$ (in $${}^ \circ C$$) is ____________.
21
A manufacturer can produce $$12000$$ bearings per day. The manufacturer received an order of $$8000$$ bearings per day from a customer. The cost of holding a bearing in stock is Rs. $$0.20$$ per month. Setup cost per production run in Rs.$$500.$$ Assuming $$300$$ working days in a year, the frequency of production run should be
22
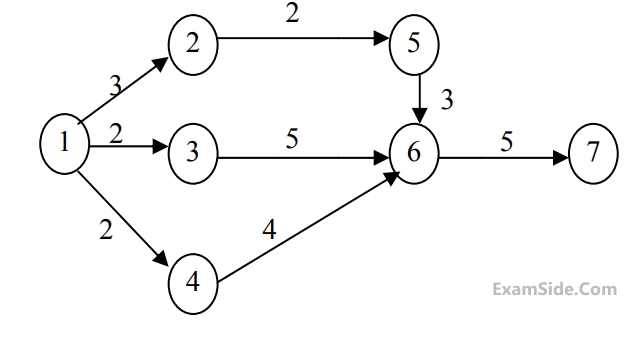
Consider the given project network, where numbers along various activities represent the normal time. The free float on activity $$4$$-$$6$$ and the project duration, respectively, are

23
The actual sales of a product in different months of a particular year are given below:


The forecast of the sales, using the 4-month moving average method, for the month of February is ____________.
24
Consider an objective function $$Z\left( {{x_1},{x_2}} \right) = 3{x_1} + 9{x_2}$$ and the constraints
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$
$$\eqalign{ & {x_1} + {x_2} \le 8, \cr & {x_1} + 2{x_2} \le 4, \cr & {x_1} \ge 0,{x_2} \ge 0, \cr} $$
The maximum value of the objective function is ________________.
25
Which one of the following is NOT correct?
26
A rotating steel shaft is supported at the ends. It is subjected to a point load at the center. The maximum bending stress developed is $$100 MPa.$$ If the yield, ultimate and corrected endurance strength of the shaft material are $$300$$ $$MPa,$$ $$500$$ $$MPa$$ and $$200$$ $$MPa,$$ respectively, then the factor of safety for the shaft is __________.
27
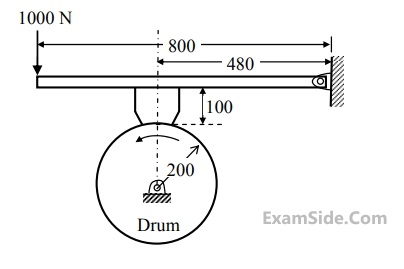
A drum brake is shown in the figure. The drum is rotating in anticlockwise direction. The coefficient of friction between drum and shoe is $$0.2.$$ The dimensions shown in the figure are in mm. The braking torque (in $$N.m$$) for the brake shoe is ________.

28
Match the casting defects (Group A) with the probable causes (Group B):


29
The hot tearing in a metal casting is due to
30
A cylindrical blind riser with diameter $$d$$ and height $$h,$$ is placed on the top of the mold cavity of a closed type sand mold as shown in the figure. If the riser is of constant volume, then the rate of solidification in the riser is the least when the ratio $$h:d$$ is 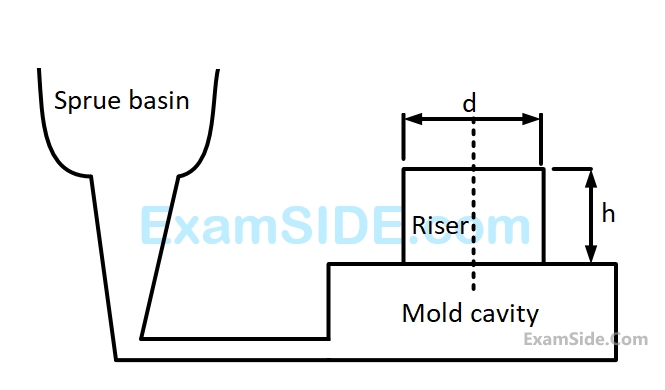

31
For spot welding of two steel sheets (base metal) each of $$3$$ $$mm$$ thickness, welding current of $$10000$$ $$A$$ is applied for $$0.2$$ $$s$$. The heat dissipated to the base metal is $$1000J.$$ Assuming that the heat required for melting $$1m{m^3}$$ volume of steel is $$20J$$ and interfacial contact resistance between sheets is $$0.0002$$$$\Omega $$, the volume (in $$m{m^3}$$) of weld nugget is _____________
32
A straight turning operation is carried out using a single point cutting tool on an $$AISI$$ $$1020$$ steel rod. The feed is $$0.2$$ $$mm/rev$$ and the depth of cut is $$0.5$$ $$mm.$$ The tool has a side cutting edge angle of $${60^ \circ }.$$ The uncut chip thickness (in $$mm$$) is _______________
33
Cutting tool is much harder than the work piece. Yet the tool wears out during the tool-work interaction, because
34
Which pair of following statement is correct for orthogonal cutting using a single-point cutting tool?
$$P.$$ reduction in friction angle increases cutting force
$$Q.$$ Reduction in friction angle decreases cutting force
$$R.$$ Reduction in friction angle increases chip thickness
$$S.$$ Reduction in friction angle decreases chip thickness
$$P.$$ reduction in friction angle increases cutting force
$$Q.$$ Reduction in friction angle decreases cutting force
$$R.$$ Reduction in friction angle increases chip thickness
$$S.$$ Reduction in friction angle decreases chip thickness
35
The diameter of a recessed ring was measured by using two spherical balls of diameter $${d_2} = 60mm$$ and $${d_1} = 40mm$$ as shown in the figure.
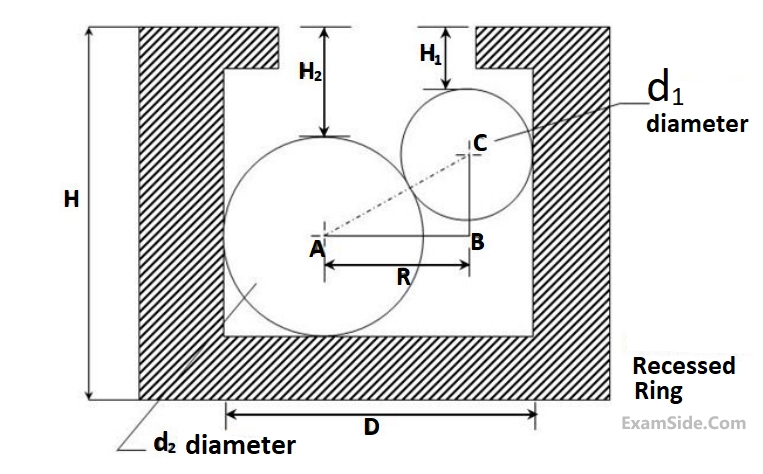

The distance $${H_2} = 35.55\,\,mm$$ and $${H_1} = 20.55\,\,mm$$. The diameter ($$D,$$ in $$mm$$) of the ring gauge is __________________.
36
The stress-strain curve for mild steel is shown in the figure given below. Choose the correct option referring to both figure and table
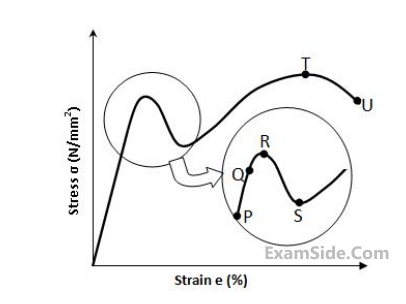
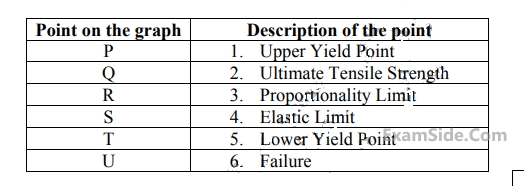


37
Consider a simply supported beam of length $$50$$h, with a rectangular cross-section of depth h, and width $$2$$h. The beam carries a vertical point load P, at its mid-point. The ratio of the maximum shear stress to the maximum bending stress in the beam is
38
Two solid circular shafts of $${{R_1}}$$ and $${{R_2}}$$ are subjected to same torque. The maximum shear stresses developed in the two shafts are $${\tau _1}$$ and $${\tau _2}.$$ If $${{{R_1}} \over {{R_2}}} = 2,$$ then $${{{\tau _1}} \over {{\tau _2}}}$$ is _______.
39
A force $$P$$ is applied at a distance $$x$$ from the end of the beam as shown in the figure. What would be the value of $$x$$ so that the displacement at $$'A'$$ is equal to zero?
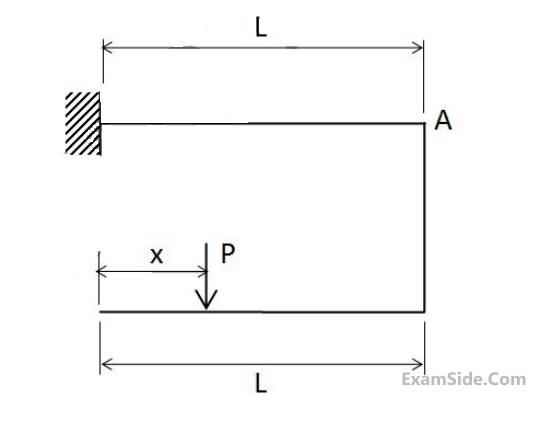

40
Consider a single degree-of-freedom system with viscous damping excited by a harmonic force. At resonance, the phase angle (in degree) of the displacement with respect to the exciting force is
41
The damping ratio of a single degree of freedom spring-mass-damper system with mass of $$1$$ kg, stiffness $$100 N/m$$ and viscous damping coefficient of $$25$$ $$N.s/m$$ is _____________
42
A mass-spring-dashpot system with mass m = 10 kg, spring constant k = 6250 N/m is excited by a harmonic excitation of 10 cos(25t) N. At the steady state, the vibration amplitude of the mass is 40mm. The damping coefficient (c, in N.s/m) of the dashpot is ______________
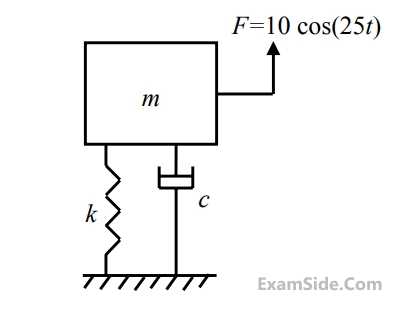

43
A certain amount of an ideal gas is initially at a pressure $${p_1}$$ and temperature $${T_1}$$. First, it undergoes a constant pressure process $$1$$-$$2$$ such that $$T{}_2 = 3{T_1}/4.$$ Then, it undergoes a constant volume process $$2$$-$$3$$ such that $${T_3} = {T_1}/2.$$ The ratio of the final volume to the initial volume of the ideal gas is
44
Which one of the following pairs of equations describes an irreversible heat engine?
45
An amount of $$100$$ $$kW$$ of heat is transferred through a wall in steady state. One side of the wall is maintained at $${127^ \circ }C$$ and the other side at $${27^ \circ }C$$. The entropy generated $$($$in $$W/K)$$ due to the heat transfer through the wall is _____________
46
A source at temperature of $$500K$$ provides $$1000$$ $$kJ$$ of heat. The temperature of environment is $${27^ \circ }C.$$ The maximum useful work (in $$kJ$$) that can be obtained from the heat source is __________
47
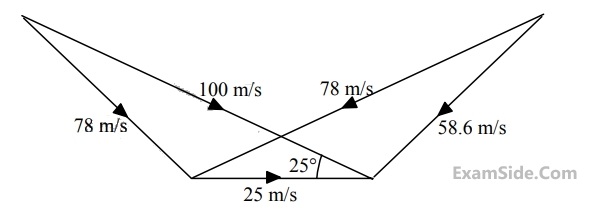
At the inlet of an axial impulse turbine rotor, the blade linear speed is 25 m/s, the magnitude of absolute velocity is 100 m/s and the angle between them is 25°. The relative velocity and the axial component of velocity remain the same between the inlet and outlet of the blades. The blade inlet and outlet velocity triangles are shown in the figure. Assuming no losses, the specific work (in J/kg) is ____________.