1
The Laplace transform of $$f\left( t \right)$$ is $${1 \over {{s^2}\left( {s + 1} \right)}}.$$
The function
2
The blasius equation $$\,{{{d^3}f} \over {d{\eta ^3}}} + {f \over 2}\,{{{d^2}f} \over {d{\eta ^2}}} = 0\,\,\,\,$$ is a
3
One of the eigen vector of the matrix $$A = \left[ {\matrix{
2 & 2 \cr
1 & 3 \cr
} } \right]$$ is
4
The parabolic are $$y = \sqrt x ,1 \le x \le 2$$ is revolved around the $$x$$-axis. The volume of the solid of revolution is
5
The function $$y = \left| {2 - 3x} \right|$$
6
The infinite series $${\,f\left( x \right) = x - {{{x^3}} \over {3!}} + {{{x^5}} \over {5!}} - {{{x^7}} \over {7!}} + - - - \,\,}$$ Converges to
7
The value of the integral $$\int\limits_{ - a}^a {{{dx} \over {1 + {x^2}}}} $$
8
A box contains $$2$$ washers, $$3$$ nuts and $$4$$ bolts. Items are drawn from the box at random one at a time without replacement. The probability of drawing $$2$$ washers first followed by $$3$$ nuts and subsequently the $$4$$ bolts is
9
A lightly loaded full journal bearing has a journal of $$50mm,$$ bush bore of $$50.50mm$$ and bush length of $$20mm.$$ if rotational speed of journal is $$1200rpm$$ and average viscosity of liquid lubricant is $$0.03$$ $$Pa$$- $$sec,$$ the power loss (in Watt) will be :
10
For the stability of a floating body, under the influence of gravity alone, which of
the following is TRUE?
11
Velocity vector of a flow fields is given as $$\overrightarrow V = 2xy\widehat i - {x^2}z\widehat j.$$ The vorticity vector at $$(1,1,1)$$ is
12
A smooth pipe of diameter $$200$$ $$mm$$ carries water. The pressure in the pipe at section
$${S_1}\,\,$$ (elevation : $$10$$ $$m$$ ) is the $$50$$ $$kPa.$$ At section
$${S_2}\,\,$$ (elevation : $$12$$ $$m$$ ) the pressure is $$20$$ $$kPa$$ and velocity is $$2$$ $$m/s.$$
Density of water is $$1000$$ $$kg/{m^3}$$ and acceleration due to gravity is $$9.8$$ $$m{s^{ - 2}}.$$ Which of the following is TRUE?
13
Maximum velocity of a one-dimensional incompressible fully developed viscous flow, between two fixed parallel plates, is $$6\,\,m{s^{ - 1}}.$$ Then mean velocity (in $$m{s^{ - 1}}$$) of the flow is
14
A fin has $$5mm$$ diameter and $$100mm$$ length. The thermal conductivity of fin material is $$400W/m K.$$ One end of the fin is maintained at $${130^ \circ }C$$ and its remaining surface is exposed to ambient air at $${30^ \circ }C.$$ if the convective heat transfer coefficient is $$40W/{m^2}K,$$ the heat loss (in $$W$$) from the fin is
15
Match the following
List-$${\rm I}$$
$$P.$$ Compressible flow
$$Q.$$ Free surface flow
$$R.$$ Boundary layer flow
$$S.$$ Pipe flow
$$T.$$ Heat convection
List-$${\rm II}$$
$$U.$$ Renolds number
$$V.$$ Nussult number
$$W.$$ Weber number
$$X.$$ Froude number
$$Y.$$ Mach number
$$Z.$$ Skin friction coefficient
16
Annual demand for window frames is $$10000.$$ Each frame costs Rs. $$200$$ and ordering cost is Rs. $$300$$ per order. Inventory holding cost is Rs. $$40$$ per frame per year. The supplier is willing to offer $$2\% $$ discount if the order quantity is $$1000$$ or more, and $$4\% $$ if order quantity is $$2000$$ or more. If the total cost is to be minimized, the retailer should
17
The project activities, precedence relationships and durations are described in the table. The critical path of the project is
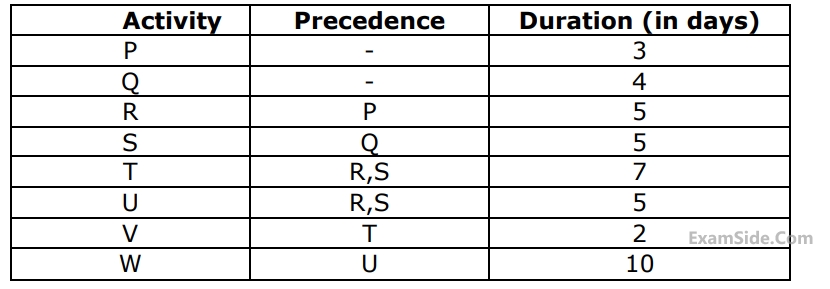
18
The demand and forecast for February are $$12000$$ and $$10275,$$ respectively. Using single exponential smoothening method (smoothening coefficient $$= 0.25$$), forecast for the month of March is
19
Little’s law is relationship between
20
Simplex method of solving linear programming problem uses
21
Four jobs are to be processed on a machine as per data listed in the table.

If the Earliest Due Date $$(EDD)$$ rule is used to sequence the jobs, the number of jobs delayed is
22
Four jobs are to be processed on a machine as per data listed in the table.

Using the Shortest Processing Time $$(SPT)$$ rule, total tardiness is
23
A bracket shown in fig. is rigidly mounted on wall using four rivets. Each rivet is $$6mm$$ in diameter and has an effective length of $$12mm.$$

Direct shear stress in $$MPa$$ in the most heavily loaded rivet is
24
Tooth interference in an external involute spur gear pair can be reduced by
25
A band brake having band-width of $$80mm,$$ drum diameter of $$250mm,$$ coefficient of friction of $$0.25$$ and angle of wrap of $$270$$ degrees is required to exert a friction torque of $$1000N$$-$$m$$. The maximum tension (in $$kN$$) developed in the band is
26
In a shear cutting operation, a sheet of $$5mm$$ thickness is cut along a length of $$200mm.$$ The cutting blade is $$400mm$$ long and zero-shear $$(S=0)$$ is provided on the edge. The ultimate shear strength of the sheet is $$100$$ $$MPa$$ and penetration to thickness ratio is $$0.2.$$ Neglect friction

Assuming force $$Vs$$ displacement curve to be rectangular, the work done in $$J$$ is
27
In a gating system, the ratio $$1:2:4$$ represents
28
For the case of molding, it is decided to replace a spherical riser of diameter $$100$$ $$mm$$ by a cylindrical riser. Determine size of the cylindrical riser that will have the identical solidification time. Assume blind risering & ratio of height to radius of cylinder is $$2.$$
29
Two steel bars each of diameter $$10mm$$ are coaxially friction welded end to end at an axial pressure of $$200MPa$$ and rotational speed of $$400rpm$$. The coefficient of friction between the mating faces of the rotating bars is $$0.50.$$ The torque is assumed to act at the $$3/{4^{th}}$$ radius of the rotating bar. The power (in $$kW$$) consumed at the interface of the welding is
30
For tool $$A,$$ Taylor’s tool life exponent $$(n)$$ is $$0.45$$ and constant $$(K)$$ is $$90.$$ Similarly for tool $$B,$$ $$n=0.3$$ and $$K=60.$$ The cutting speed (in $$m/min$$) above which tool $$A$$ will have a higher tool life than tool $$B$$ is
31
In a shear cutting operation, a sheet of $$5mm$$ thickness is cut along a length of $$200mm.$$ The cutting blade is $$400mm$$ long and zero-shear $$(S=0)$$ is provided on the edge. The ultimate shear strength of the sheet is $$100$$ $$MPa$$ and penetration to thickness ratio is $$0.2.$$ Neglect friction

A shear of $$20mm$$ $$(S=20mm)$$ is now provided on the blade. Assuming force $$Vs$$ displacement curve to be trapezoidal, the maximum force (in $$kN$$) exerted is
32
A shaft has a dimension $$\phi $$ $${35^{\matrix{
{ - 0.009} \cr
{ - 0.025} \cr
} }}$$. The respective values of fundamental deviation and tolerance are
33
A taper hole is inspected using a $$CMM,$$ with a probe of $$2mm$$ diameter. At a height, $$Z=10mm$$ from the bottom, $$5$$ points are touched and a diameter of circle (not compensated for probe size) is obtained as $$20mm.$$ similarly, a $$40mm$$ diameter is btained at a height $$Z=40mm.$$ The smaller diameter (in $$mm$$) of hole at $$Z=0$$ is

34
In a $$CNC$$ program block, $$N002\,\,\,\,G02\,\,\,\,G91\,\,\,\,X40\,\,\,\,Z40....,\,\,\,\,G02\,\,\,\,\& \,\,\,\,G91$$ refer to
35
The state of plane-stress at a point is given by $${\sigma _x}\,\, = 200$$ MPa, $${\sigma _x}\,\, = 100$$ MPa and $${\tau _{xy}} = 100$$ MPa. The maximum shear stress (in MPa) is
36
Which of the following statements is INCORRECT
37
There are two points P and Q on a planar rigid body. The relative velocity between the two points
38
Mobility of a statically indeterminate structure is
39
For the configuration shown, the angular velocity of link AB is $$10$$ rad/s counterclockwise. The magnitude of the relative sliding velocity (in ms
-1) of slider B with respect to rigid link CD is

40
Tooth interference in an external involute spur gear pair can be reduced by
41
For the epicyclic gear arrangement shown in the figure, $${{\omega _2} = 100}$$ rad/s clockwise (CW) and $${{\omega _{arm}} = 80}$$ rad/s counter clockwise (CCW). The angular velocity $${{\omega _5}}$$ (in rad/s) is
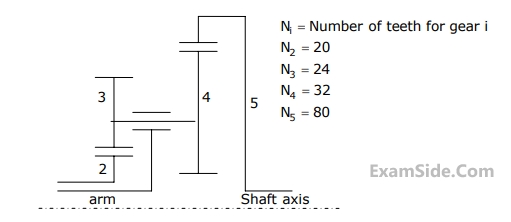
42
The natural frequency of a spring-mass system on earth is $${\omega _n}.$$ The natural frequency of this system on the moon (gmoon = gearth/6) is
43
A mass $$m$$ attached to a spring is subjected to a harmonic force as shown in the figure. The amplitude of the forced motion is observed to be $$50$$ mm. The value of m (in kg) is
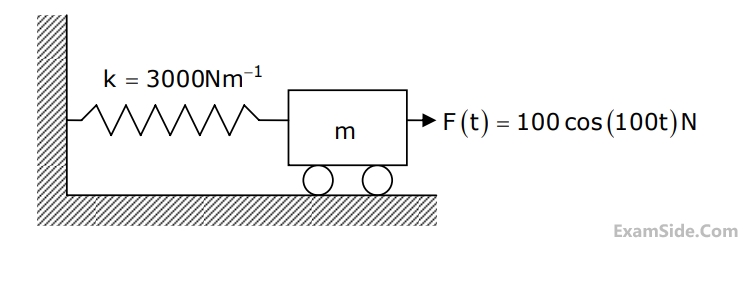
44
A mono-atomatic ideal gas $$\left( {\gamma = 1.67,} \right.$$ molecular weight$$=40$$ $$\left. \, \right)$$ is compressed adiabatically from $$0.1$$ $$MPa,$$ $$300K$$ to $$0.2$$ $$MPa.$$ The universal gas constant is $$8.314$$ $$kJ$$ $$kmo{l^{ - 1}}{K^{ - 1}}.$$ The work of compression of the gas (in $$kJ$$ $$k{g^{ - 1}}$$) is
45
One kilogram of water at room temperature is brought into contact with a high temperature thermal reservoir. The entropy change of the universe is
46
Consider the following two processes;
$$\left( {\rm I} \right)$$ A heat source at $$1200$$ $$K$$ loses $$2500$$ $$kJ$$ of heat to a sink at $$800$$ $$K$$
$$\left( {\rm II} \right)$$ A heat source at $$800$$ $$K$$ loses $$2000$$ $$kJ$$ of heat to a sink at $$500$$ $$K$$
Which of the following statements is true?
47
In a steam power plant operating on the Rankine cycle, steam enters the turbine at $$4$$ $$MPa,$$ $${350^ \circ }C$$ and exits at a pressure of $$15$$ $$kPa.$$ Then it enters the condenser and exits as saturated water. Next, a pump feeds back the water to the boiler. The adiabatic efficiency of the turbine is $$90\% $$. The thermodynamic states of water and steam are given in the table.

$$h$$ is specific enthalpy, $$s$$ is specific entropy and $$v$$ the specific volume; subscripts $$f$$ and $$g$$ denote saturated liquid state and saturated vapour state.
The net work output $$(kJ/kg)$$ of the cycle is
48
In a steam power plant operating on the Rankine cycle, steam enters the turbine at $$4$$ $$MPa,$$ $${350^ \circ }C$$ and exits at a pressure of $$15$$ $$kPa.$$ Then it enters the condenser and exits as saturated water. Next, a pump feeds back the water to the boiler. The adiabatic efficiency of the turbine is $$90\% $$. The thermodynamic states of water and steam are given in the table.

$$h$$ is specific enthalpy, $$s$$ is specific entropy and $$v$$ the specific volume; subscripts $$f$$ and $$g$$ denote saturated liquid state and saturated vapour state.
Heat supplied $$(kJ/kg)$$ to the cycle is
49
A phenomenon is modeled using $$n$$ dimensional variables with $$k$$ primary dimensions. The number of non-dimensional variables is
50
A hydraulic turbine develops $$1000$$ $$kW$$ power for a head of $$40$$ $$m.$$ If the head is reduced to $$20$$ $$m,$$ the power developed (in $$kW$$) is











