Two coins are tossed simultaneously. The probability (upto two decimal points accuracy) of getting at least one head is _________.

The determinant of a $$2 \times 2$$ matrix is $$50.$$ If one eigenvalue of the matrix is $$10,$$ the other eigenvalue is __________.

Consider the matrix $$A = \left[ {\matrix{ {50} & {70} \cr {70} & {80} \cr } } \right]$$ whose eigenvectors corresponding to eigen values $${\lambda _1}$$ and $${\lambda _2}$$ are $${x_1} = \left[ {\matrix{ {70} \cr {{\lambda _1} - 50} \cr } } \right]$$ and $${x_2} = \left[ {\matrix{ {{\lambda _2} - 80} \cr {70} \cr } } \right],$$ respectively. The value of $$x_1^T{x_2}$$ is ________

The surface integral $$\int {\int\limits_s {F.ndS} } $$ over the surface $$S$$ of the sphere $${x^2} + {y^2} + {z^2} = 9,$$ where $$\,F = \left( {x + y} \right){\rm I} + \left( {x + z} \right)j + \left( {y + z} \right)k\,\,$$ and $$n$$ is the unit outward surface normal, yields ___________.

A simple of $$15$$ data is as follows; $$17,18,17,17,13,18,5,5,6,7,8,9,20,17,3.$$ The mode of the data is

Consider the differential equation $$\,\,3y''\left( x \right) + 27y\left( x \right) = 0\,\,$$ with initial conditions $$y\left( 0 \right) = 0$$ and $$y'\left( 0 \right) = 2000.\,\,$$ The value of $$y$$ at $$x=1$$ is __________.

If $$f\left( z \right) = \left( {{x^2} + a{y^2}} \right) + ibxy$$ is a complex analytic function of $$z=x+iy,$$
where $${\rm I} = \sqrt { - 1} ,$$ then

The rod PQ of length L = 2 m, and uniformly distributed mass of M = 10 kg, is released from rest at the position shown in the figure. The ends slide along the frictionless faces OP and OQ. Assume acceleration due to gravity, g = 10 m/s² . The mass moment of inertia of the rod about its centre of mass and an axis perpendicular to the plane of the figure is (ML² /12). At this instant, the magnitude of angular acceleration (in radian/s² ) of the rod is ____________.

A $$60$$ $$mm$$ $$-$$ diameter water jet strikes a plate containing a hole of $$40mm$$ diameter as shown in the figure. Part of the jet passes through the hole horizontally, and the remaining is deflected vertically. The density of water is $$1000$$ $$kg/{m^3}$$ . If velocities are as indicated in the figure, the magnitude of horizontal force (in $$N$$) required to hold the plate is _______________

Consider a laminar flow at zero over a flat plate . The shear stress at the wall is denoted by $${\tau _w}.$$ The axial positions $${x_1}$$ and $${x_2}$$ on the plate are measured from the leading edge in the direction of flow. If $${x_2} > {x_1},$$ then

The arrangement shown in the figure measures the velocity $$V$$ of a gas of density $$1kg/{m^3}$$ flowing through a pipe. The acceleration due to gravity is $$9.81m/{s^2}.$$ If the manometric fluid is water (density $${1000kg/{m^3}}$$ ) and the velocity $$V$$ is $$20 m/s,$$ the differential head $$h$$ (in $$mm$$) between the two arms of the manometer is ______.

For the stability of a floating body the

The heat loss from a fin is $$6W.$$ The effectiveness of the fin are $$3$$ and $$0.75,$$ respectively. The heat loss (in $$W$$) from the fin, keeping the entire fin surface at base temperature, is ___________________

A metal ball of diameter $$60mm$$ is initially at $${220^ \circ }C.$$ The ball is suddenly cooled by an air jet of $${20^ \circ }C.$$ The heat transfer coefficient is $$200\,W/{m^2}.K.$$ The specific heat, thermal conductivity and density of the metal ball are $$400\,\,J/kg.K,\,\,400\,\,W/m.K$$ and $$\,9000\,\,kg/{m^3},$$ respectively. The ball temperature (in $${}^ \circ C$$) after $$90$$ seconds will be approximately.

The emissive power of a blackbody is $$P.$$ If its absolute temperature is doubled, the emissive power becomes

In a counter-flow heat exchanger, water is heated at the rate of $$1.5kg/s$$ from $$\,40{}^ \circ C\,$$ to $$\,80{}^ \circ C\,$$ by an oil entering at $$\,120{}^ \circ C\,$$ and leaving at $$\,60{}^ \circ C\,$$. The specific heats of water and oil are $$4.2kJ/kgK$$ and $$2kJ/kgK,$$ respectively. The overall heat transfer coefficient is $$400\,W/{m^2}K.$$ The required heat transfer surface are (in $${m^2}$$) is

The standard deviation of linear dimensions $$P$$ and $$Q$$ are $$3\mu m$$ and $$4\mu m$$, respectively. When assembled, the standard deviation (in $$\mu m$$) of the following linear dimension $$(P+Q)$$ is ___________.

A project starts with activity $$A$$ and ends with activity $$F.$$ The precedence relation and durations of the activities are as per the following table:

The minimum project completion time (in days) is ___________

For a single server with Poisson arrival and exponential service time, the arrival rate is $$12$$ per hour. Which one of the following service rates will provide a steady state finite queue length?

Maximize $$\,\,\,\,\,\,\,\,\,Z = 5{x_1} + 3{x_2}$$
Subject to $$\,\,\,\,\,\,\,\,\,\,{x_1} + 2{x_2} \le 10,$$
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1} - {x_2} \le 8, \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_1},{x_2} \ge 0 \cr} $$

In the starting simplex tableau, $${x_1}$$ and $${x_2}$$ are non-basic variables and the value of $$Z$$ is zero. The value of $$Z$$ in the next simplex tableau is __________________.

A product made in two factories $$P$$ and $$Q,$$ is transported to two destinations, $$R$$ and $$S.$$ The per unit costs of transportation (in Rupees) from factories to destinations are as per the following matrix.

Factory $$P$$ produces $$7$$ units and factory $$Q$$ produces $$9$$ units of the product. Each destination requires $$8$$ units. If the north-west corner method provides the total transportation cost as $$X$$ (in Rupees) and the optimized (the minimum) total transportation cost $$Y$$ (in Rupees), then $$(X$$-$$Y),$$ in Rupees, is

The principal stresses at a point in a critical section of a machine component are $${\sigma _1} = 60\,\,MPa,\,\,{\sigma _2} = 5\,\,MPa$$ and $${\sigma _3} = - 40\,\,MPa.$$ For the material of the component, the tensile yield strength is $${\sigma _y} = 200\,\,MPa.$$ According to the maximum shear stress theory, the factor of safety is

A machine component made of a ductile material is subjected to a variable loading with $${\sigma _{\min }} = - 50MPa$$ and $${\sigma _{\max }} = 50MPa.$$ If the corrected endurance limit and the yield strength for the material are $$\sigma {'_e}$$ $$100MPa$$ and $${\sigma _y} = 300MPa,$$ respectively, the factor of safety is __________.

A steel plate, connected to a fixed channel using three identical bolts $$A, B$$ and $$C,$$ carries a load of $$6kN$$ as shown in the figure. Considering the effect of direct load and moment, the magnitude of resultant shear force (in $$kN$$) on bolt $$C$$ is.

A single – plate clutch has a friction disc with inner and outer radii of $$20mm$$ and $$40$$ $$mm,$$ respectively. The friction lining in the disc is made in such a way that the coefficient of friction $$\mu $$ varies radially as $$ = 0.01\,r,$$ where $$r$$ is in $$mm.$$ The clutch needs to transmit a friction torque of $$18.85$$ $$kN.mm.$$ As per uniform pressure theory, the pressure (in $$MPa$$) on the disc is ___________________.

It is desired to make a product having T-shaped cross - section from a rectangular aluminium block. Which one of the following processes is expected to provide the highest strength of the product?

A strip of $$120mm$$ width and $$8mm$$ thickness is rolled between two $$300$$ $$mm$$-diameter rolls to get a strip of $$120mm$$ width and $$7.2mm$$ thickness. The speed of the strip at the exit is $$30m/min.$$ There is no front or back tension. Assuming uniform roll pressure of $$200$$ $$MPa$$ in the roll bite and $$100\% $$ mechanical efficiency, the minimum total power (in $$kW$$) required to drive the two rolls is ____________________

A rod of length $$20$$ $$mm$$ is stretched to make a rod of length $$40$$ $$mm.$$ Subsequently, it is compressed to make a rod of final length $$10$$ $$mm.$$ Consider the longitudinal tensile strain as positive and compressive strain as negative. The total true longitudinal strain in the rod is

During the turning of a $$20$$ $$mm-$$diameter steel bar at a spindle speed of $$400$$ $$rpm,$$ a tool life of $$20$$ minute is obtained. When the same bar is turned at $$200$$ $$rpm,$$ the tool life becomes $$60$$ $$minute.$$ Assume that Taylor's tool life equation is valid. When the bar is turned at $$300$$ $$rpm,$$ the tool life (in minute) is approximately

In an orthogonal machining with a tool of $${9^ \circ }$$ orthogonal rake angle, the uncut chip thickness is $$0.2$$ $$mm.$$ The chip thickness fluctuates between $$0.25$$ $$mm$$ and $$0.4$$ $$mm.$$ The ratio of the maximum shear angle to the minimum shear angle during machining is ______________

A cylindrical pin $$25_{ + 0.010}^{ + 0.020}\,\,mm$$ diameter is electroplated. Plating thickness is
$${2.0^{ \pm 0.005}}\,\,mm$$. Neglecting the gauge tolerance, the diameter (in $$mm,$$ up to $$3$$ decimal points accuracy) of the $$GO$$ ring gauge to inspect the plated pin is ___________

A steel bar is held by two fixed supports as shown in the figure and is subjected to an increases of temperature $$\Delta T = {100^ \circ }C.$$ If the coefficient of thermal expansion and Young's modulus of elasticity of steel are $$11 \times {10^{ - 6}}/{}^ \circ C$$ and $$200$$GPa, respectively, the magnitude of thermal stress (in MPa) induced in the bar is __________.

The state of stress at a point is $${\sigma _x} = {\sigma _y} = {\sigma _z} = {\tau _{xz}} = {\tau _{zx}} = {\tau _{yz}} = {\tau _{zy}} = 0$$ and $${\tau _{xy}} = {\tau _{yx}} = 50$$MPa. The maximum normal stress (in MPa) at the point is _________.

For a loaded cantilever beam of uniform cross-section, the bending moment (in N-mm) along the length is M(x) = 5x²+10x, where x is the distance (in mm) measured from the free end of the beam. The magnitude of shear force (in N) in the cross-section at x=10mm is _________.

A helical compression spring made of wire of circular cross-section is subjected to a compressive load. The maximum shear stress induced in the cross-section of the wire is 24 MPa. For the same compressive load, if both the wire diameter and the mean coil diameter are doubled, the maximum shear stress (in MPa) induced in the cross-section of the wire is _____.

A cantilever beam of length $$L$$ and flexural modulus $$EI$$ is subjected to a point load $$P$$ at the free end. The elastic strain energy stored in the beam due to bending (neglecting transverse shear) is

In a slider-crank mechanism, the lengths of the crank and the connecting rod are 100mm and 160mm, respectively. The crank is rotating with an angular velocity of 10 radian/s counter-clockwise. The magnitude of linear velocity (in m/s) of the piston at the instant corresponding to the configuration shown in the figure is _____________

Block 2 slides outward on link 1 at a uniform velocity of 6m/s as shown in the figure. Link 1 is rotating at a constant angular velocity of 20 radian/s counterclockwise. The magnitude of the total acceleration (in m/s² ) of point P of the block with respect to fixed point O is ____________

A gear train shown in the figure consists of gears P, Q, R and S. Gear Q and gear R are mounted on the same shaft. All the gears are mounted on parallel shafts and the number of teeth of P, Q, R and S are 24, 45, 30 and 80, respectively. Gear P is rotating at 400 rpm. The speed (in rpm) of the gear S is _________ .

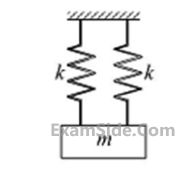
A mass $$m$$ is attached to two identical springs having spring constant $$k$$ as shown in the figure. The natural frequency of this single degree of freedom system is

The radius of gyration of a compound pendulum about the point of suspension is $$100$$ mm. The distance between the point of suspension and the centre of mass is $$250$$ mm. Considering the acceleration due to gravity as $$9.81$$ m/s², the natural frequency (in radian/s) of the compound pendulum is _________.

In the Rankine cycle for a system power plant the turbine entry and exit enthalpies are $$2803$$ $$kJ/kg$$ and $$1800$$ $$kJ/kg$$, respectively. The enthalpies of water at pump entry and exit are $$121$$ $$kJ/kg$$ and $$124$$ $$kJ/kg,$$ respectively. The specific steam consumption (in $$kg/kW.h$$) of the cycle is __________.

The volume and temperature of air (assumed to be an ideal gas) in a closed vessel is $$2.87{m^3}$$ and $$300$$ $$K,$$ respectively. The gauge pressure indicated by a manometer fitted to the wall of the vessel is $$0.5$$ bar. If the gas constant of air is
$$R =287J/kgK$$ and the atmospheric pressure is $$1$$ bar, the mass of air (in $$kg$$) in the vessel is

A calorically perfect gas (specific heat at constant pressure $$1000$$$$J/kg.K$$) enters and leaves a gas turbine with the same velocity. The temperatures of the gas at turbine entry and exit are $$1100K$$ and $$400K.$$ respectively. The power produced is $$4.6MW$$ and heat escapes at the rate of $$300kJ/s$$ through the turbine casing. The mass flow rate of the gas (in $$kg/s$$) through the turbine is.

A mass $$m$$ of a perfect gas at pressure $${p_1}$$ and volume $${V_1}$$ undergoes an isothermal process. The final pressure is $${p_2}$$ and volume is $${V_2}.$$ The work done on the system is considered positive. If $$R$$ is the gas constant and $$T$$ is the temperature, then the work done in the process is

One $$kg$$ of an ideal gas (gas constant $$R=287$$ $$J/kg$$-$$K$$) undergoes an irreversible process from state- $${\rm I}$$ ( $$1$$ bar, $$300$$ $$K$$ ) to state-$$2$$ ( $$2$$ bar, $$300$$ $$K$$). The change in specific entropy $$\left( {{s_2} - {s_1}} \right)$$ of the gas (in $$J/kg$$.$$K$$) in the process is ____________

Which one of the following statement is TRUE?