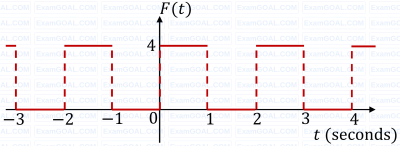
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?

Consider a cube of unit edge length and sides parallel to co-ordinate axes, with its centroid at the point (1, 2, 3). The surface integral $\int_A \vec{F}.d\vec{A}$ of a vector field $\vec{F}=3x\hat{i}+5y\hat{j}+6z\hat{k}$ over the entire surface A of the cube is ______.

Consider the definite integral

$\int^2_1(4x^2+2x+6)dx$

Let I_e be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is I_s. The percentage error is defined as e = 100 × (I_e - I_s)/I_e The value of e is

Given $\int^{\infty}_{-\infty}e^{-x^2}dx=\sqrt{\pi}$

If a and b are positive integers, the value of $\int^{\infty}_{-\infty}e^{-a(x+b)^2}dx$ is _________.

A polynomial ψ(s) = a_nsⁿ + a_n-1s^n-1 + ......+ a₁s + a₀ of degree n > 3 with constant real coefficients a_n, a_n-1, ... a₀ has triple roots at s = -σ. Which one of the following conditions must be satisfied?

For the exact differential equation,

$\frac{du}{dx}=\frac{-xu^2}{2+x^2u}$

which one of the following is the solution?

A is a 3 × 5 real matrix of rank 2. For the set of homogeneous equations Ax = 0, where 0 is a zero vector and x is a vector of unknown variables, which of the following is/are true?

If the sum and product of eigenvalues of a 2 × 2 real matrix $\begin{bmatrix}3&p\\\ p&q\end{bmatrix} $ are 4 and -1 respectively, then |p| is _______ (in integer).

Given z = x +iy, i = √-1 C is a circle of radius 2 with the centre at the origin. If the contour C is traversed anticlockwise, then the value of the integral $\frac{1}{2\pi}\int_c\frac{1}{(z-i)(z+4i)}dZ$ is ________ (round off to one decimal place.)

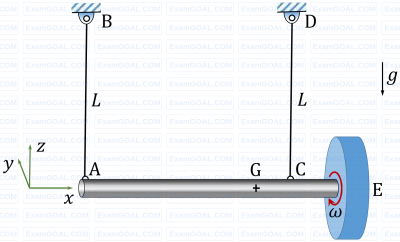
A massive uniform rigid circular disc is mounted on a frictionless bearing at the end E of a massive uniform rigid shaft AE which is suspended horizontally in a uniform gravitational field by two identical light inextensible strings AB and CD as shown, where G is the center of mass of the shaft-disc assembly and g is the acceleration due to gravity. The disc is then given a rapid spin w about its axis in the positive xaxis direction as shown, while the shaft remains at rest. The direction of rotation is defined by using the right-hand thumb rule. If the string AB is suddenly cut, assuming negligible energy dissipation, the shaft AE will

Match the additive manufacturing technique in Column I with its corresponding input material in Column II.

Additive manufacturing technique (Column I)		Input Material  (Column II)
P.	Fused deposition modeling	1.	Photosensitive liquid resin
Q.	Laminated object Manufacturing	2.	Heat fusible power
R.	Selective laser sintering	3.	Filament of polymer
		4.	Sheet of thermoplastic or green compacted metal sheet

A square plate is supported in four different ways (configurations (P) to (S) as shown in the figure). A couple moment C is applied on the plate. Assume all the members to be rigid and mass-less, and all joints to be frictionless. All support links of the plate are identical.

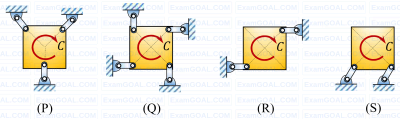
The square plate can remain in equilibrium in its initial state for which one or more of the following support configurations?

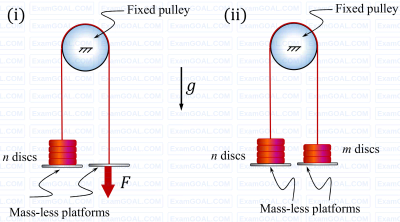
A rope with two mass-less platforms at its two ends passes over a fixed pulley as shown in the figure. Discs with narrow slots and having equal weight of 20 N each can be placed on the platforms. The number of discs placed on the left side platform is n and that on the right side platform is m.

It is found that for n = 5 and m = 0, a force F= 200 N (refer to part (i) of the figure) is just sufficient to initiate upward motion of the left side platform. If the force F is removed then the minimum value of m (refer to part (ii) of the figure) required to prevent downward motion of the left side platform is (in integer).

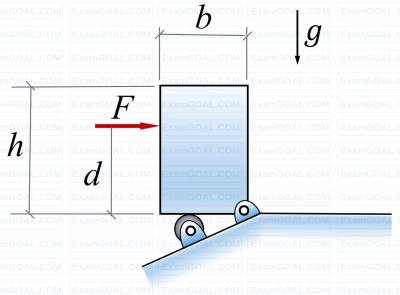
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s²), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse I_F is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of I_F required to topple the block is

A rigid body in the X-Y plane consists of two point masses (1 kg each) attached to the ends of two massless rods, each of 1 cm length, as shown in the figure. It rotates at 30 RPM counter-clockwise about the Z-axis passing through point O. A point mass of √2 kg, attached to one end of a third massless rod, is used for balancing the body by attaching the free end of the rod to point O. The length of the third rod is ______ cm.

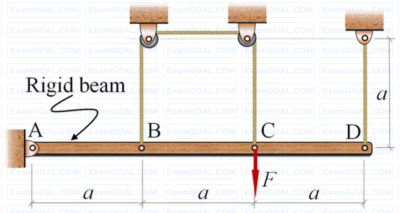
A rigid beam AD of length 3a = 6 m is hinged at frictionless pin joint A and supported by two strings as shown in the figure. String BC passes over two small frictionless pulleys of negligible radius. All the strings are made of the same material and have equal cross-sectional area. A force F = 9 KN is applied at C and the resulting stresses in the strings are within linear elastic limit. The self-weight of the beam is negligible with respect to the applied load. Assuming small deflections, the tension developed in the string at C is KN (round off to 2 decimal places).

The lengths of members BC and CE in the frame shown in the figure are equal. All the members are rigid and lightweight, and the friction at the joints is negligible. Two forces of magnitude Q > 0 are applied as shown, each at the mid-length of the respective member on which it acts.

Which one or more of the following members do not carry any load (force)?

Consider a steady flow through a horizontal divergent channel, as shown in the figure, with the supersonic flow at the inlet. The direction of flow is from left to right.

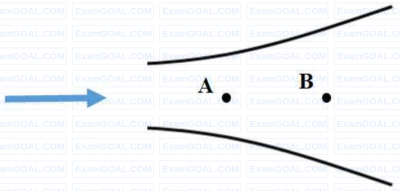
Pressure at location B is observed to be higher than that at an upstream location A. Which among the following options can be the reason?

The velocity field in a fluid is given to be $\vec{V}=(4xy)\hat{i}+2(x^2-y^2)\hat{j}$ Which of the following statement(s) is/are correct?

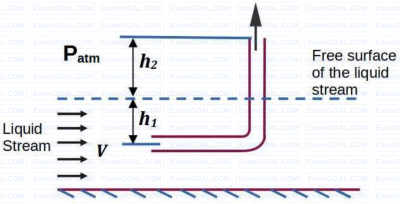
A tube of uniform diameter D is immersed in a steady flowing inviscid liquid stream of velocity V, as shown in the figure. Gravitational acceleration is represented by g. The volume flow rate through the tube is ______.

The steady velocity field in an inviscid fluid of density 1.5 is given to be $\vec{V}=(y^2-x^2)\hat{i}+(2xy)\hat{j} $. Neglecting body forces, the pressure gradient at (x =1, y = 1) is ______.

A uniform wooden rod (specific gravity = 0.6, diameter = 4 cm and length = 8 m) is immersed in the water and is hinged without friction at point A on the waterline as shown in the figure. A solid spherical ball made of lead (specific gravity = 11.4) is attached to the free end of the rod to keep the assembly in static equilibrium inside the water. For simplicity, assume that the radius of the ball is much smaller than the length of the rod.

Assume density of water = 10³ kg/m³ and π = 3.14.

Radius of the ball is _______ cm (round off to 2 decimal places).

Which of the following non-dimensional terms is an estimate of Nusselt number?

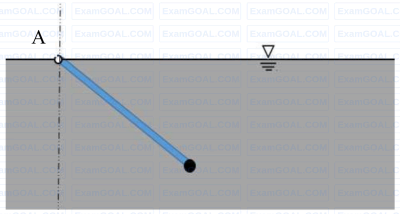
Wien’s law is stated as follows: λ_mT = C, where C is 2898 μm.K and λ_m is the wavelength at which the emissive power of a black body is maximum for a given temperature T. The spectral hemispherical emissivity (ε_λ) of a surface is shown in the figure below (1 Å = 10^-10 m). The temperature at which the total hemispherical emissivity will be highest is K (round off to the nearest integer).

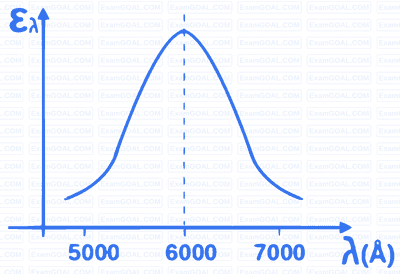
Consider steady state, one-dimensional heat conduction in an infinite slab of thickness 2L (L = 1 m) as shown in the figure. The conductivity (k) of the material varies with temperature as k = CT, where T is the temperature in K, and C is a constant equal to 2 W.m^-1K^-2. There is a uniform heat generation of 1280 kW/m³ in the slab. If both faces of the slab are maintained at 600 K, then the temperature at x = 0 is _______ K (in integer).

Saturated vapor at 200 °C condenses to saturated liquid at the rate of 150 kg/s on the shell side of a heat exchanger (enthalpy of condensation h_fg = 2400 kJ/kg). A fluid with C_p = 4 kJ-kg^-1K^-1. enters at 100 °C on the tube side. If the effectiveness of the heat exchanger is 0.9, then the mass flow rate of the fluid in the tube side is __________ kg/s (in integer). 

Consider a hydrodynamically and thermally fully-developed, steady fluid flow of 1 kg/s in a uniformly heated pipe with diameter of 0.1 m and length of 40 m. A constant heat flux of magnitude 15000 W/m² is imposed on the outer surface of the pipe. The bulk-mean temperature of the fluid at the entrance to the pipe is 200 °C. The Reynolds number (Re) of the flow is 85000, and the Prandtl number (Pr) of the fluid is 5. The thermal conductivity and the specific heat of the fluid are 0.08 w.m¹K^-1 and 2600 J-kg¹K^-1, respectively. The correlation Nu = 0.023 Re^0.8 Pr^0.4 is applicable, where the Nusselt Number (Nu) is defined on the basis of the pipe diameter. The pipe surface temperature at the exit is _______ °C (round off to the nearest integer).

An electric car manufacturer underestimated the January sales of car by 20 units, while the actual sales was 120 units. If the manufacturer uses exponential smoothing method with a smoothing constant of α = 0.2, then the sales forecast for the month of February of the same year is ______ units (in integer). 

The demand of a certain part is 1000 parts/year and its cost is Rs. 1000/part. The orders are placed based on the economic order quantity (EOQ). The cost of ordering is Rs. 100/order and the lead time for receiving the orders is 5 days. If the holding cost is Rs. 20/part/year, the inventory level for placing the orders is _______ parts (round off to the nearest integer).

Parts P1 - P7 are machined first on a milling machine and then polished at a separate machine. Using the information in the following table, the minimum total completion time required for carrying out both the operations for all 7 parts is _______ hours.

Part	Milling (hours)	Polishing (hours)
P1	8	6
P2	3	2
P3	3	4
P4	4	6
P5	5	7
P6	6	4
P7	2	1

A project consists of five activities (A, B, C, D and E). The duration of each activity follows beta distribution. The three time estimates (in weeks) of each activity and immediate predecessor(s) are listed in the table. The expected time of the project completion is ______ weeks (in integer).

Activity	Time estimates (in weeks)			Immediate predecessor(s)
	Optimistic time	Most likely time	Pessimistic time
A	4	5	6	None
B	1	3	5	A
C	1	2	3	A
D	2	4	6	C
E	3	4	5	B, D

A manufacturing unit produces two products Pl and P2. For each piece of P1 and P2, the table below provides quantities of materials M1, M2, and M3 required, and also the profit earned. The maximum quantity available per day for M1, M2 and M3 is also provided. The maximum possible profit per day is ₹ ______

	M1	M2	M3	Profit per piece ( ₹)
P1	2	2	0	150
P2	3	1	2	100
Maximum quantity available per day	70	50	40

Which one of the following CANNOT impart linear motion in a CNC machine?

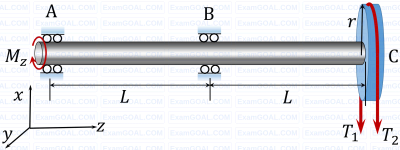
A shaft AC rotating at a constant speed carries a thin pulley of radius r = 0.4 m at the end C which drives a belt. A motor is coupled at the end A of the shaft such that it applies a torque M, about the shaft axis without causing any bending moment. The shaft is mounted on narrow frictionless bearings at A and B where AB = BC = L = 0.5 m. The taut and slack side tensions of the belt are T₁ = 300 N and T₂ = 100 N, respectively. The allowable shear stress for the shaft material is 80 MPa. The self-weights of the pulley and the shaft are negligible. Use the value of π available in the on-screen virtual calculator. Neglecting shock and fatigue loading and assuming maximum shear stress theory, the minimum required shaft diameter is mm (round off to 2 decimal places).

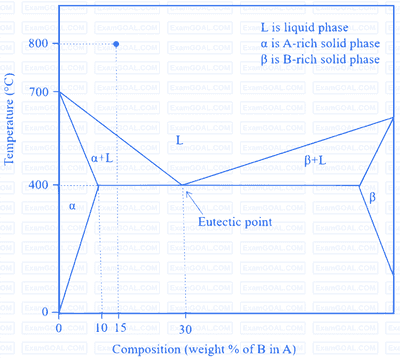
Fluidity of a molten alloy during sand casting depends on its solidification range. The phase diagram of a hypothetical binary alloy of components A and B is shown in the figure with its eutectic composition and temperature. All the lines in this phase diagram, including the solidus and liquidus lines, are straight lines. If this binary alloy with 15 weight % of B is poured into a mould at a pouring temperature of 800 °C, then the solidification range is

A shaft of diameter $25^{-0.04}_{-0.07}$ mm is assembled in a hole of diameter $25^{+0.02}_{-0.00}$ mm. Match the allowance and limit parameter in Column I with its corresponding quantitative value in Column II for this shaft-hole assembly.

Allowance and limit parameter (Column I)		Quantitative value (Column II)
P.	Allowance	1.	0.09 mm
Q.	Maximum clearance	2.	24.96 mm
R.	Maximum material limit for hole	3.	0.04 mm
		4.	25.0 mm

Consider sand casting of a cube of edge length a. A cylindrical riser is placed at the top of the casting. Assume solidification time, t_s ∝ V/A, where V is the volume and A is the total surface area dissipating heat. If the top of the riser is insulated, which of the following radius/radii of riser is/are acceptable?

Which of these processes involve(s) melting in metallic workpieces?

A straight-teeth horizontal slab milling cutter is shown in the figure. It has 4 teeth and diameter (D) of 200 mm. The rotational speed of the cutter is 100 rpm and the linear feed given to the workpiece is 1000 mm/minute. The width of the workpiece (w) is 100 mm, and the entire width is milled in a single pass of the cutter. The cutting force/tooth is given by F = Kt_cw, where specific cutting force K = 10 N/mm², w is the width of cut, and t_c is the uncut chip thickness.

The depth of cut (d) is D/2, and hence the assumption of $\frac{d}{D}<<1$ is invalid. The maximum cutting force required is ______ KN (round off to one decimal place).

In an orthogonal machining operation, the cutting and thrust forces are equal in magnitude. The uncut chip thickness is 0.5 mm and the shear angle is 15°. The orthogonal rake angle of the tool is 0° and the width of cut is 2 mm. The workpiece material is perfectly plastic and its yield shear strength is 500 MPa. The cutting force is _______ N (round off to the nearest integer).

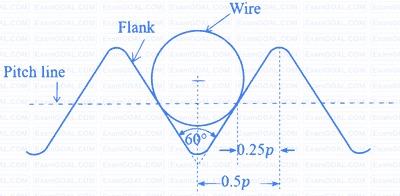
The best size wire is fitted in a groove of a metric screw such that the wire touches the flanks of the thread on the pitch line as shown in the figure. The pitch (p) and included angle of the thread are 4 mm and 60°, respectively. The diameter of the best size wire is _________ mm (round off to 2 decimal places).

In a direct current arc welding process, the power source has an open circuit voltage of 100 V and short circuit current of 1000 A. Assume a linear relationship between voltage and current. The arc voltage (V) varies with the arc length (l) as V = 10 + 5l where V is in volts and l is in mm. The maximum available arc power during the process is ______ kVA (in integer).

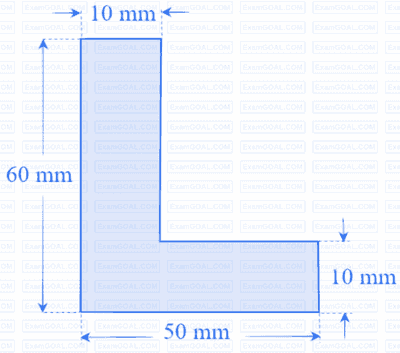
A cylindrical billet of 100 mm diameter and 100 mm length is extruded by a direct extrusion process to produce a bar of L-section. The cross sectional dimensions of this L-section bar are shown in the figure. The total extrusion pressure (p) in MPa for the above process is related to extrusion ratio (r) as

$\rm p=K_s σ_m\left[0.8+1.5\ ln(r)+\frac{2l}{d_0}\right] $

where σ_m, is the mean flow strength of the billet material in MPa, l is the portion of the billet length remaining to be extruded in mm, d₀ is the initial diameter of the billet in mm, and K_s is the die shape factor.

If the mean flow strength of the billet material is 50 MPa and the die shape factor is 1.05, then the maximum force required at the start of extrusion is _______ kN (round off to one decimal place).

Which one of the following is the definition of ultimate tensile strength (UTS) obtained from a stress-strain test on a metal specimen?

A structural member under loading has a uniform state of plane stress which in usual notations is given by σ_x = 3P, σ_y = -2P and τ_xy = √2 P, where P > 0. The yield strength of the material is 350 MPa. If the member is designed using the maximum distortion energy theory, then the value of P at which yielding starts (according to the maximum distortion energy theory) is

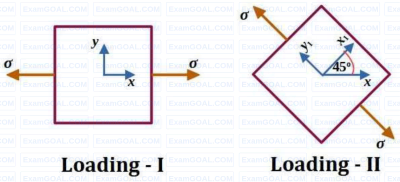
A linear elastic structure under plane stress conditions is subjected to two sets of loading, I and II. The resulting states of stress at a point corresponding to these two loadings are as shown in the figure below. If these two sets of loading are applied simultaneously, then the net normal component of stress σ_xx is ________

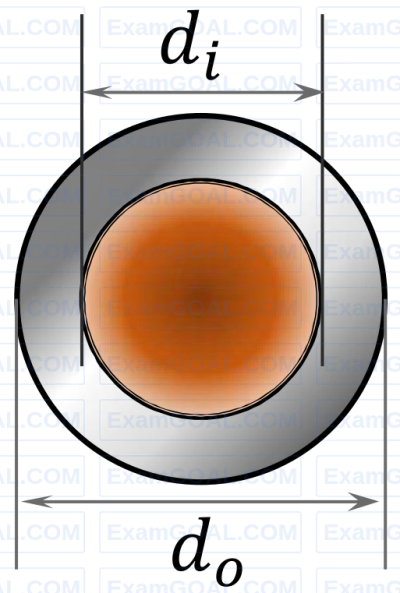
A shaft of length L is made of two materials, one in the inner core and the other in the outer rim, and the two are perfectly joined together (no slip at the interface) along the entire length of the shaft. The diameter of the inner core is d; and the external diameter of the rim is d₀, as shown in the figure. The modulus of rigidity of the core and rim materials are G_i and G₀, respectively. It is given that d₀ = 2d_i and G_i = 3G₀. When the shaft is twisted by application of a torque along the shaft axis, the maximum shear stress developed in the outer rim and the inner core turn out to be τ₀ and τ_i, respectively. All the deformations are in the elastic range and stress-strain relations are linear. Then the ratio τ_i/τ₀ is (round off to 2 decimal places).

For a dynamical system governed by the equation,

$\ddot{x}(t)+2 ζ \omega_n \dot{x}(t)+\omega_n^2x(t)=0$

the damping ratio ζ is equal to $\frac{1}{2\pi}\log_e2$. The displacement x of this system is measured during a hammer test. A displacement peak in the positive displacement direction is measured to be 4 mm. Neglecting higher powers (> 1) of the damping ratio, the displacement at the next peak in the positive direction will be _______ mm (in integer).

A spring mass damper system (mass m, stiffness k, and damping coefficient c) excited by a force F(t) = B sin ωt, where B, ω and t are the amplitude, frequency and time, respectively, is shown in the figure. Four different responses of the system (marked as (i) to (iv)) are shown just to the right of the system figure. In the figures of the responses, A is the amplitude of response shown in red color and the dashed lines indicate its envelope. The responses represent only the qualitative trend and those are not drawn to any specific scale.

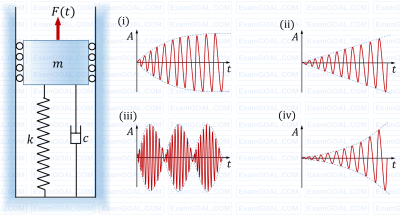
Four different parameter and forcing conditions are mentioned below.

(P) c > 0 and $ω=\sqrt{k/m}$

(Q) c < 0 and ω ≠ 0

(R) c = 0 and $\omega=\sqrt{k/m}$

(S) c = 0 and $\omega \cong\sqrt{k/m}$

Which one of the following options gives correct match (indicated by arrow →) of the parameter and forcing conditions to the responses?

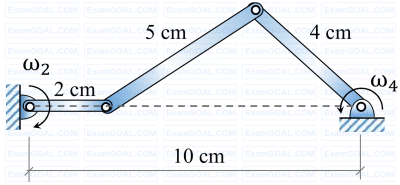
In the configuration of the planar four-bar mechanism at a certain instant as shown in the figure, the angular velocity of the 2 cm long link is ω₂ = 5 rad/s. Given the dimensions as shown, the magnitude of the angular velocity ω₄ of the 4 cm long link is given by rad/s (round off to 2 decimal places).

Which one of the following is an intensive property of a thermodynamic system?

Consider 1 kg of an ideal gas at 1 bar and 300 K contained in a rigid and perfectly insulated container. The specific heat of the gas at constant volume c_v is equal to 750 J-kg^-1K^-1. A stirrer performs 225 kJ of work on the gas. Assume that the container does not participate in the thermodynamic interaction. The final pressure of the gas will be ______ bar (in integer). 

In a vapour compression refrigeration cycle, the refrigerant enters the compressor in saturated vapour state at evaporator pressure, with specific enthalpy equal to 250 kJ/kg. The exit of the compressor is superheated at condenser pressure with specific enthalpy equal to 300 kJ/kg. At the condenser exit, the refrigerant is throttled to the evaporator pressure. The coefficient of performance (COP) of the cycle is 3. If the specific enthalpy of the saturated liquid at evaporator pressure is 50 kJ/kg, then the dryness fraction of the refrigerant at entry to evaporator is ________.

A rigid tank of volume of 8 m³ is being filled up with air from a pipeline connected through a valve. Initially the valve is closed and the tank is assumed to be completely evacuated. The air pressure and temperature inside the pipeline are maintained at 600 kPa and 306 K, respectively. The filling of the tank begins by opening the valve and the process ends when the tank pressure is equal to the pipeline pressure. During the filling process, heat loss to the surrounding is 1000 kJ. The specific heats of air at constant pressure and at constant volume are 1.005 kJ/kg.K and 0.718 kJ/kg.K, respectively. Neglect changes in kinetic energy and potential energy.

The final temperature of the tank after the completion of the filling process is ________ K (round off to the nearest integer). 

At steady state, 500 kg/s of steam enters a turbine with specific enthalpy equal to 3500 kJ/kg and specific entropy equal to 6.5 kJ-kg^-1K^-1. It expands reversibly in the turbine to the condenser pressure. Heat loss occurs reversibly in the turbine at a temperature of 500 K. If the exit specific enthalpy and specific entropy are 2500 kJ/kg and 6.3 kJ-kg^-1K^-1, respectively, the work output from the turbine is _________ MW (in integer).

Direction: Fill in the blank spaces in the given sentence selecting an appropriate set of words from the following options-

Writing too many things on the ______ while teaching could make the students get ______.

Which one of the following is a representation (not to scale and in bold) of all values of x satisfying the inequality $2-5x\leq-\left(\frac{6x-5}{3}\right)\;$ on the real number line?

If $f(x)=2\ln(\sqrt{e^x})$, what is the area bounded by f(x) for the interval [0, 2] on the x-axis?

A person was born on the fifth Monday of February in a particular year. Which one of the following statements is correct based on the above information?

Which one of the groups given below can be assembled to get the shape that is shown above using each piece only once without overlapping with each other? (rotation and translation operations may be used).

Fish belonging to species S in the deep sea have skins that are extremely black (ultra-black skin). This helps them not only to avoid predators but also sneakily attack their prey. However, having this extra layer of black pigment results in lower collagen on their skin, making their skin more fragile.

Which one of the following is the CORRECT logical inference based on the information in the above passage?  

For the past m days, the average daily production at a company was 100 units per day.

If today’s production of 180 units changes the average to 110 units per day, what is the value of m?

Consider the following functions for non-zero positive integers, p and q.

$\rm f(p,q)=\frac{p\times p\times p\times.......\times p}{q\ terms}=p^q;\;$; f(p, 1) = p

$g(p,q)=p^{p^{p^{p^{p^{..^{..^{..^{up\ to\ q\ terms}}}}}}}}$; g(p, 1) = p

Which one of the following options is correct based on the above? 

Four cities P, Q, R and S are connected through one-way routes as shown in the figure. The travel time between any two connected cities is one hour. The boxes beside each city name describe the starting time of first train of the day and their frequency of operation. For example, from city P, the first trains of the day start at 8 AM with a frequency of 90 minutes to each of R and S. A person does not spend additional time at any city other than the waiting time for the next connecting train.

If the person starts from R at 7 AM and is required to visit S and return to R, what is the minimum time required?

Equal sized circular regions are shaded in a square sheet of paper of 1 cm side length. Two cases, case M and case N, are considered as shown in the figures below. In the case M, four circles are shaded in the square sheet and in the case N, nine circles are shaded in the square sheet as shown.

What is the ratio of the areas of unshaded regions of case M to that of case N?