The limit

$\rm p = \displaystyle\lim_{x \rightarrow \pi} \left( \frac{x^2 + α x + 2 \pi^2}{x - \pi + 2 \sin x} \right)$

has a finite value for a real α. The value of α and the corresponding limit p are

Solution of ∇²T = 0 in a square domain (0 < x < 1 and 0 < y < 1) with boundary conditions:

T(x, 0) = x; T(0, y) = y; T(x, 1) = 1 + x; T(1, y) = 1 + y is

Given a function $\rm ϕ = \frac{1}{2} (x^2 + y^2 + z^2) $ in three-dimensional Cartesian space, the value of the surface integral

∯_S n̂ . ∇ϕ dS

where S is the surface of a sphere of unit radius and n̂ is the outward unit normal vector on S, is

The Fourier series expansion of x³ in the interval −1 ≤ x < 1 with periodic continuation has

If A = $\begin{bmatrix} 10 & 2k + 5 \\\ 3k - 3 & k + 5 \end{bmatrix} $ is a symmetric matrix, the value of k is _______.

The value of the integral

$\rm \oint \left( \frac{6z}{2z^4 - 3z^3 + 7 z^2 - 3z + 5} \right) dz$

evaluated over a counter-clockwise circular contour in the complex plane enclosing only the pole z = i, where 𝑖 is the imaginary unit, is

The system of linear equations in real (x, y) given by

$\rm \begin{pmatrix} \rm x & \rm y \end{pmatrix} \begin{bmatrix} 2 & 5- 2 α \\\ α & 1 \end{bmatrix} = \rm \begin{pmatrix} \rm 0 & \rm 0 \end{pmatrix} $

involves a real parameter α and has infinitely many non-trivial solutions for special value(s) of α. Which one or more among the following options is/are non-trivial solution(s) of (x, y) for such special value(s) of α ?

Let a random variable X follow Poisson distribution such that

Prob(X = 1) = Prob(X = 2).

The value of Prob(X = 3) is __________ (round off to 2 decimal places).

Consider two vectors

$\rm \vec a = 5 i + 7 j + 2 k $

$\rm \vec b = 3i - j + 6k$

Magnitude of the component of $\vec a$ orthogonal to $\vec b$ in the plane containing the vectors $\vec a$ and $\vec{\bar b}$ is ______ (round off to 2 decimal places).

The plane of the figure represents a horizontal plane. A thin rigid rod at rest is pivoted without friction about a fixed vertical axis passing through O. Its mass moment of inertia is equal to 0.1 kg∙cm2 about O. A point mass of 0.001 kg hits it normally at 200 cm/s at the location shown, and sticks to it. Immediately after the impact, the angular velocity of the rod is ___________ rad/s (in integer).

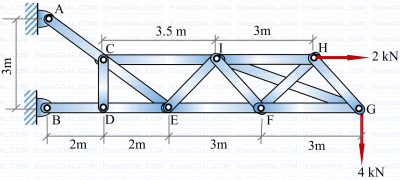
A structure, along with the loads applied on it, is shown in the figure. Self-weight of all the members is negligible and all the pin joints are friction-less. AE is a single member that contains pin C. Likewise, BE is a single member that contains pin D. Members GI and FH are overlapping rigid members. The magnitude of the force carried by member CI is ________ kN (in integer).

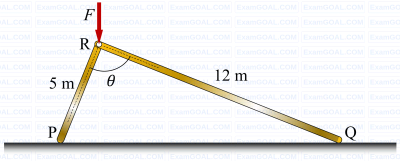
Two rigid massless rods PR and RQ are joined at frictionless pin-joint R and are resting on ground at P and Q, respectively, as shown in the figure. A vertical force F acts on the pin R as shown. When the included angle 𝜃 < 90°, the rods remain in static equilibrium due to Coulomb friction between the rods and ground at locations P and Q. At 𝜃 = 90°, impending slip occurs simultaneously at points P and Q. Then the ratio of the coefficient of friction at Q to that at P (μQ /μP) is _________ (round off to two decimal places).

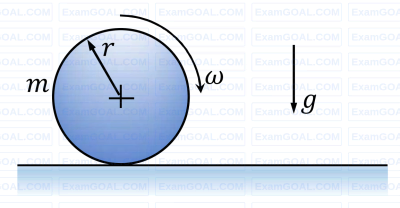
A cylindrical disc of mass m = 1 kg and radius r = 0.15 m was spinning at 𝜔 = 5 rad/s when it was placed on a flat horizontal surface and released (refer to the figure). Gravity g acts vertically downwards as shown in the figure. The coefficient of friction between the disc and the surface is finite and positive. Disregarding any other dissipation except that due to friction between the disc and the surface, the horizontal velocity of the center of the disc, when it starts rolling without slipping, will be _________ m/s (round off to 2 decimal places).

A tiny temperature probe is fully immersed in a flowing fluid and is moving with zero relative velocity with respect to the fluid. The velocity field in the fluid is $\vec V = (2x) \hat i + (y + 3t) \hat j,$ and the temperature field in the fluid is T = 2x² + xy + 4t, where x and y are the spatial coordinates, and t is the time. The time rate of change of temperature recorded by the probe at (x = 1, y = 1, t = 1) is _______.

In the following two-dimensional momentum equation for natural convection over a surface immersed in a quiescent fluid at temperature T_∞ (g is the gravitational acceleration, β is the volumetric thermal expansion coefficient, ν is the kinematic viscosity, u and v are the velocities in x and y directions, respectively, and T is the temperature)

$\rm u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = g β (T - T_∞) + \nu \frac{\partial^2 u}{\partial y^2} $

the term gβ(T - T_∞) represent

The figure shows a purely convergent nozzle with a steady, inviscid compressible flow of an ideal gas with constant thermophysical properties operating under choked condition. The exit plane shown in the figure is located within the nozzle. If the inlet pressure (P0) is increased while keeping the back pressure (Pback) unchanged, which of the following statements is/are true?

A solid spherical bead of lead (uniform density = 11000 kg/m³) of diameter d = 0.1 mm sinks with a constant velocity V in a large stagnant pool of a liquid (dynamic viscosity = 1.1 × 10^-3 kg∙m^-1∙s^-1). The coefficient of drag is given by $\rm C_D = \frac{24}{Re} $, where the Reynolds number (Re) is defined on the basis of the diameter of the bead. The drag force acting on the bead is expressed as $\rm D = (C_D) (0.5 \rho V^2) \left( \frac{\pi d^2}{4} \right), $ where ρ is the density of the liquid. Neglect the buoyancy force. Using g = 10 m/s², the velocity V is __________ m/s.

Consider steady, one-dimensional compressible flow of a gas in a pipe of diameter 1 m. At one location in the pipe, the density and velocity are 1 kg/m³ and 100 m/s, respectively. At a downstream location in the pipe, the velocity is 170 m/s. If the pressure drop between these two locations is 10 kPa, the force exerted by the gas on the pipe between these two locations is _______ N.

A steady two-dimensional flow field is specified by the stream function

ψ = kx3y,

where x and y are in meters and the constant k = 1 m-2s-1. The magnitude of acceleration at a point (x, y) = (1 m, 1 m) is ________ m/s2 (round off to 2 decimal places).

A flat plate made of cast iron is exposed to a solar flux of 600 W/m² at an ambient temperature of 25 °C. Assume that the entire solar flux is absorbed by the plate. Cast iron has a low-temperature absorptivity of 0.21. Use Stefan-Boltzmann constant = 5.669 × 10^-8 W/m²-K⁴. Neglect all other modes of heat transfer except radiation. Under the aforementioned conditions, the radiation equilibrium temperature of the plate is __________ °C (round off to the nearest integer).

Consider a rod of uniform thermal conductivity whose one end (x = 0) is insulated and the other end (x = L) is exposed to flow of air at temperature T_∞ with convective heat transfer coefficient h. The cylindrical surface of the rod is insulated so that the heat transfer is strictly along the axis of the rod. The rate of internal heat generation per unit volume inside the rod is given as 

$\rm \dot q = \cos \frac{2 \pi x}{L}$

The steady-state temperature at the mid-location of the rod is given as T_A. What will be the temperature at the same location, if the convective heat transfer coefficient increases to 2h?

Consider a solid slab (thermal conductivity, k = 10 W∙m^-1∙K^-1) with thickness 0.2 m and of infinite extent in the other two directions as shown in the figure. Surface 2, at 300 K, is exposed to a fluid flow at a free stream temperature (T_∞) of 293 K, with a convective heat transfer coefficient (h) of 100 W∙m^-2∙K^-1. Surface 2 is opaque, diffuse and gray with an emissivity (ε) of 0.5 and exchanges heat by radiation with very large surroundings at 0 K. Radiative heat transfer inside the solid slab is neglected. The Stefan-Boltzmann constant is 5.67 × 10^-8 W∙m^-2∙K^-4. The temperature T₁ of Surface 1 of the slab, under steady-state conditions, is _________ K (round off to the nearest integer).

During open-heart surgery, a patient’s blood is cooled down to 25 °C from 37 °C using a concentric tube counter-flow heat exchanger. Water enters the heat exchanger at 4 °C and leaves at 18 °C. Blood flow rate during the surgery is 5 L/minute.

Use the following fluid properties :

$$ \begin{array}{|c|c|c|} \hline \text { Fluid } & \text { Density }\left(\mathrm{kg} / \mathrm{m}^3\right) & \text { Specific heat }(\mathrm{J} / \mathrm{kg}-\mathrm{K}) \\ \hline \text { Blood } & 1050 & 3740 \\ \hline \text { Water } & 1000 & 4200 \\ \hline \end{array} $$

Effectiveness of the heat exchanger is _________ (round off to 2 decimal places).

In a linear programming problem, if a resource is not fully utilized, the shadow price of that resource is

Which one of the following is NOT a form of inventory?

Activities A to K are required to complete a project. The time estimates and the immediate predecessors of these activities are given in the table. If the project is to be completed in the minimum possible time, the latest finish time for the activity G is ______ hours.

$$ \begin{array}{|c|c|c|} \hline \text { Activity } & \text { Time (hours) } & \text { Immediate predecessors } \\ \hline \text { A } & 2 & - \\ \hline \text { B } & 3 & - \\ \hline \text { C } & 2 & - \\ \hline \text { D } & 4 & \text { A } \\ \hline \text { E } & 5 & \text { B } \\ \hline \text { F } & 4 & \text { B } \\ \hline \text { G } & 3 & \text { C } \\ \hline \text { H } & 10 & \text { D, E } \\ \hline \text { I } & 5 & \text { F } \\ \hline \text { J } & 8 & \text { G } \\ \hline \text { K } & 3 & \text { H, I, J } \\ \hline \end{array} $$

An assignment problem is solved to minimize the total processing time of four jobs (1, 2, 3 and 4) on four different machines such that each job is processed exactly by one machine and each machine processes exactly one job. The minimum total processing time is found to be 500 minutes. Due to a change in design, the processing time of Job 4 on each machine has increased by 20 minutes. The revised minimum total processing time will be ________ minutes (in integer).

The product structure diagram shows the number of different components required at each level to produce one unit of the final product P. If there are 50 units of on hand inventory of component A, the number of additional units of component A needed to produce 10 units of product P is _________ (in integer).

A square threaded screw is used to lift a load W by applying a force F. Efficiency of square threaded screw is expressed as

A CNC worktable is driven in a linear direction by a lead screw connected directly to a stepper motor. The pitch of the lead screw is 5 mm. The stepper motor completes one full revolution upon receiving 600 pulses. If the worktable speed is 5 m/minute and there is no missed pulse, then the pulse rate being received by the stepper motor is

The type of fit between a mating shaft of diameter $25.0^{\begin{matrix} +0.010 \\\ -0.010 \end{matrix}}$ mm and a hole of diameter $25.0^{\begin{matrix} +0.015 \\\ -0.015 \end{matrix}}$ is ______.

Which of the following methods can improve the fatigue strength of a circular mild steel (MS) shaft?

A bracket is attached to a vertical column by means of two identical rivets U and V separated by a distance of 2a = 100 mm, as shown in the figure. The permissible shear stress of the rivet material is 50 MPa. If a load P = 10 kN is applied at an eccentricity e = 3√7 a, the minimum cross-sectional area of each of the rivets to avoid failure is ___________ mm².

Which of the following heat treatment processes is/are used for surface hardening of steels?

Which of the following additive manufacturing technique(s) can use a wire as a feedstock material?

Electrochemical machining operations are performed with tungsten as the tool, and copper and aluminum as two different workpiece materials. Properties of copper and aluminum are given in the table below.

$$ \begin{array}{|c|c|c|c|} \hline \text { Material } & \begin{array}{l} \text { Atomic mass } \\ \text { (amu) } \end{array} & \text { Valency } & \text { Density }\left(\mathrm{g} / \mathrm{cm}^3\right) \\ \hline \text { Copper } & 63 & 2 & 9 \\ \hline \text { Aluminum } & 27 & 3 & 2.7 \\ \hline \end{array} $$

Ignore overpotentials, and assume that current efficiency is 100% for both the
workpiece materials. Under identical conditions, if the material removal rate (MRR) of copper is 100 mg/s, the MRR of aluminum will be ________________ mg/s (round-off to two decimal places).

Under orthogonal cutting condition, a turning operation is carried out on a metallic workpiece at a cutting speed of 4 m/s. The orthogonal rake angle of the cutting tool is 5º. The uncut chip thickness and width of cut are 0.2 mm and 3 mm, respectively. In this turning operation, the resulting friction angle and shear angle are 45º and 25º, respectively. If the dynamic yield shear strength of the workpiece material under this cutting condition is 1000 MPa, then the cutting force is _______ N (round off to one decimal place).

A 1 mm thick cylindrical tube, 100 mm in diameter, is orthogonally turned such that the entire wall thickness of the tube is cut in a single pass. The axial feed of the tool is 1 m/minute and the specific cutting energy (u) of the tube material is 6 J/mm³. Neglect contribution of feed force towards power. The power required to carry out this operation is _________ kW (round off to one decimal place).

A 4 mm thick aluminum sheet of width w = 100 mm is rolled in a two-roll mill of roll diameter 200 mm each. The workpiece is lubricated with a mineral oil, which gives a coefficient of friction, μ = 0.1. The flow stress (σ) of the material in MPa is σ = 207 + 414 𝜀, where 𝜀 is the true strain. Assuming rolling to be a plane strain deformation process, the roll separation force (F) for maximum permissible draft (thickness reduction) is _________ kN (round off to the nearest integer).

Use:

 $F = 1.15 \barσ \left( 1 + \frac{\mu L}{2 \bar h} \right)$ wL, where $\bar \sigma$ is average flow stress, L is roll-workpiece contact length, and $\bar h$ is the average sheet thickness

Two mild steel plates of similar thickness, in butt-joint configuration, are welded by gas tungsten arc welding process using the following welding parameters.

$$ \begin{array}{|l|l|} \hline \text { Welding voltage } & 20 \mathrm{~V} \\ \hline \text { Welding current } & 150 \mathrm{~A} \\ \hline \text { Welding speed } & 5 \mathrm{~mm} / \mathrm{s} \\ \hline \end{array} $$

A filler wire of the same mild steel material having 3 mm diameter is used in this welding process. The filler wire feed rate is selected such that the final weld bead is composed of 60% volume of filler and 40% volume of plate material. The heat required to melt the mild steel material is 10 J/mm3. The heat transfer factor is 0.7 and melting factor is 0.6. The feed rate of the filler wire is __________ mm/s (round off to one decimal place).

A uniform light slender beam AB of section modulus EI is pinned by a frictionless joint A to the ground and supported by a light inextensible cable CB to hang a weight W as shown. If the maximum value of W to avoid buckling of the beam AB is obtained as βπ²EI, where π is the ratio of circumference to diameter of a circle, then the value of β is

An L-shaped elastic member ABC with slender arms AB and BC of uniform crosssection is clamped at end A and connected to a pin at end C. The pin remains in continuous contact with and is constrained to move in a smooth horizontal slot. The section modulus of the member is same in both the arms. The end C is subjected to a horizontal force P and all the deflections are in the plane of the figure. Given the length AB is 4a and length BC is 𝑎, the magnitude and direction of the normal force on the pin from the slot, respectively, are

A thin-walled cylindrical pressure vessel has mean wall thickness of t and nominal radius of r. The Poisson’s ratio of the wall material is 1/3. When it was subjected to some internal pressure, its nominal perimeter in the cylindrical portion increased by 0.1% and the corresponding wall thickness became t̅. The corresponding change in the wall thickness of the cylindrical portion, i.e. 100 × (t̅ − t)/t, is ________% (round off to 3 decimal places).

The figure shows a schematic of a simple Watt governor mechanism with the spindle O₁O₂ rotating at an angular velocity ω about a vertical axis. The balls at P and S have equal mass. Assume that there is no friction anywhere and all other components are massless and rigid. The vertical distance between the horizontal plane of rotation of the balls and the pivot O₁ is denoted by h. The value of h = 400 mm at a certain ω. If ω is doubled, the value of h will be _________ mm.

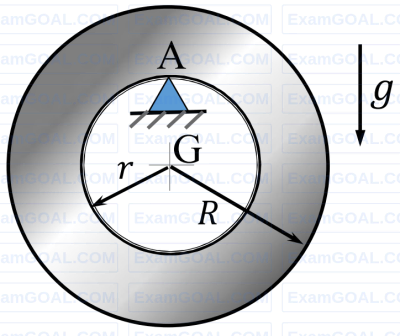
A rigid uniform annular disc is pivoted on a knife edge A in a uniform gravitational field as shown, such that it can execute small amplitude simple harmonic motion in the plane of the figure without slip at the pivot point. The inner radius r and outer radius 𝑅 are such that r² = R²/2, and the acceleration due to gravity is g. If the time period of small amplitude simple harmonic motion is given by $T = β π \sqrt{R/g} $ where π is the ratio of circumference to diameter of a circle, then β = ________ (round off to 2 decimal places).

A planar four-bar linkage mechanism with 3 revolute kinematic pairs and 1 prismatic kinematic pair is shown in the figure, where AB ⊥ CE and FD ⊥ CE. The T-shaped link CDEF is constructed such that the slider B can cross the point D, and CE is sufficiently long. For the given lengths as shown, the mechanism is

Consider a forced single degree-of-freedom system governed by $\rm \ddot x(t) + 2 ζ ω_n \dot x (t) + ω_n^2 x(t) = ω_n^2 \cos (ω t)$, where ζ and ω_n are the damping ratio and undamped natural frequency of the system, respectively, while ω is the forcing frequency. The amplitude of the forced steady state response of this system is given by [(1 − r²)² + (2ζr)²]^-1/2, where 𝑟 = ω/ωn. The peak amplitude of this response occurs at a frequency  ω =  ω_p. If  ω_d denotes the damped natural frequency of this system, which one of the following options is true?

A schematic of an epicyclic gear train is shown in the figure. The sun (gear 1) and planet (gear 2) are external, and the ring gear (gear 3) is internal. Gear 1, gear 3 and arm OP are pivoted to the ground at O. Gear 2 is carried on the arm OP via the pivot joint at P, and is in mesh with the other two gears. Gear 2 has 20 teeth and gear 3 has 80 teeth. If gear 1 is kept fixed at 0 rpm and gear 3 rotates at 900 rpm counter clockwise (ccw), the magnitude of angular velocity of arm OP is __________rpm (in integer).

The Clausius inequality holds good for

A polytropic process is carried out from an initial pressure of 110 kPa and volume of 5 m³ to a final volume of 2.5 m³. The polytropic index is given by n = 1.2. The absolute value of the work done during the process is _______ kJ (round off to 2 decimal places).

In Fe-Fe₃C phase diagram, the eutectoid composition is 0.8 weight % of carbon at 725 ºC. The maximum solubility of carbon in α-ferrite phase is 0.025 weight % of carbon. A steel sample, having no other alloying element except 0.5 weight % of carbon, is slowly cooled from 1000 ºC to room temperature. The fraction of pro-eutectoid α-ferrite in the above steel sample at room temperature is

Consider a one-dimensional steady heat conduction process through a solid slab of thickness 0.1 m. The higher temperature side A has a surface temperature of 80 °C, and the heat transfer rate per unit area to low-temperature side B is 4.5 kW/m². The thermal conductivity of the slab is 15 W/m.K. The rate of entropy generation per unit area during the heat transfer process is ________ W/m².K (round off to 2 decimal places).

In a steam power plant based on Rankine cycle, steam is initially expanded in a high-pressure turbine. The steam is then reheated in a reheater and finally expanded in a low-pressure turbine. The expansion work in the high-pressure turbine is 400 kJ/kg and in the low-pressure turbine is 850 kJ/kg, whereas the pump work is 15 kJ/kg. If the cycle efficiency is 32%, the heat rejected in the condenser is ________ kJ/kg (round off to 2 decimal places).

An engine running on an air standard Otto cycle has a displacement volume 250 cm³ and a clearance volume 35.7 cm³. The pressure and temperature at the beginning of the compression process are 100 kPa and 300 K, respectively. Heat transfer during constant-volume heat addition process is 800 kJ/kg. The specific heat at constant volume is 0.718 kJ/kg.K and the ratio of specific heats at constant pressure and constant volume is 1.4. Assume the specific heats to remain constant during the cycle. The maximum pressure in the cycle is ______ kPa (round off to the nearest integer).

After playing _________ hours of tennis, I am feeling _________ tired to walk back.

The average of the monthly salaries of M, N and S is ₹ 4000. The average of the monthly salaries of N, S and P is ₹ 5000. The monthly salary of P is ₹ 6000. What is the monthly salary of M as a percentage of the monthly salary of P?

A person travelled 80 km in 6 hours. If the person travelled the first part with a uniform speed of 10 kmph and the remaining part with a uniform speed of 18 kmph.

What percentage of the total distance is travelled at a uniform speed of 10 kmph?

Four girls P, Q, R and S are studying languages in a University. P is learning French and Dutch. Q is learning Chinese and Japanese. R is learning Spanish and French. S is learning Dutch and Japanese.

Given that: French is easier than Dutch; Chinese is harder than Japanese; Dutch is easier than Japanese, and Spanish is easier than French.

Based on the above information, which girl is learning the most difficult pair of languages?

A block with a trapezoidal cross-section is placed over a block with rectangular cross section as shown above.

Which one of the following is the correct drawing of the view of the 3D object as viewed in the direction indicated by an arrow in the above figure?

Humans are naturally compassionate and honest. In a study using strategically placed wallets that appear “lost”, it was found that wallets with money are more likely to be returned than wallets without money. Similarly, wallets that had a key and money are more likely to be returned than wallets with the same amount of money alone. This suggests that the primary reason for this behavior is compassion and empathy.

Which one of the following is the CORRECT logical inference based on the information in the above passage?

A rhombus is formed by joining the midpoints of the sides of a unit square.

What is the diameter of the largest circle that can be inscribed within the rhombus?

An equilateral triangle, a square and a circle have equal areas.

What is the ratio of the perimeters of the equilateral triangle to square to circle?

Given below are three conclusions drawn based on the following three statements.

Statement 1 : All teachers are professors.

Statement 2 : No professor is a male.

Statement 3 : Some males are engineers.

Conclusion I : No engineer is a professor.

Conclusion II : Some engineers are professors.

Conclusion III : No male is a teacher.

Which one of the following options can be logically inferred?

In a 12-hour clock that runs correctly, how many times do the second, minute, and hour hands of the clock coincide, in a 12-hour duration from 3 PM in a day to 3 AM the next day?