The inverse Laplace transform of $${1 \over {\left( {{s^2} + s} \right)}}$$ is

An analytic function of a complex variable $$z = x + i\,y$$ is expressed as
$$f\left( z \right) = u\left( {x,y} \right) + i\,\,v\,\,\left( {x,y} \right)$$ where $$i = \sqrt { - 1} .$$
If $$u=xy$$ then the expression for $$v$$ should be

The divergence of the vector field $$\,3xz\widehat i + 2xy\widehat j - y{z^2}\widehat k$$ at a point $$(1,1,1)$$ is equal to

For a matrix $$\left[ M \right] = \left[ {\matrix{ {{3 \over 5}} & {{4 \over 5}} \cr x & {{3 \over 5}} \cr } } \right].$$ The transpose of the matrix is equal to the inverse of the matrix, $${\left[ M \right]^T} = {\left[ M \right]^{ - 1}}.$$ The value of $$x$$ is given by

The distance between the origin and the point nearest to it on the surface $$\,\,{z^2} = 1 + xy\,\,$$ is

The area enclosed between the curves $${y^2} = 4x\,\,$$ and $${{x^2} = 4y}$$ is

If three coins are tossed simultaneously, the probability of getting at least one head is

The standard deviation of a uniformly distributed random variable $$b/w$$ $$0$$ and $$1$$ is

The solution of $$x{{dy} \over {dx}} + y = {x^4}$$ with condition $$y\left( 1 \right) = {6 \over 5}$$

A uniform rigid rod of mass $$M$$ and length $$L$$ is hinged at one end as shown in theadjacent figure. A force P is applied at a distance of $$2L/3$$ from the hinge so thatthe rod swings to the right. The reaction at the hinge is

A block weighing 981 $$N$$ is resting on a horizontal surface. The coefficient of friction between the block and the horizontal surface is $$\mu = 0.2.$$ A vertical cable attached to the block provides partial support as shown. A man can pull horizontally with a force of 100 $$N$$. What will be the tension, $$T$$ (inN) in the cable if the man is just able to move the block to the right?

Water at $${25^0}C$$ is flowing through a $$1.0km$$ long $$G.I.$$ pipe of $$200mm$$ diameter at the rate of $$0.07$$ $${m^3}/s.$$ If value of Darcy friction factor for this pipe is $$0.02$$ and density of water is $$1000\,\,kg/{m^3}$$, the pumping power (in $$kW$$) required to maintain the flow is

You are asked to evaluate assorted fluid flows for their suitability in a given laboratory application. The following three flow choices. Expressed in terms of the two - dimensional velocity fields in the $$x-$$ $$y$$ plane, are made available.
$$P:$$ $$u = 2y,\,\,\,v = - 3x$$
$$Q:$$ $$u=3xy,$$ $$\,\,\,\,$$$$v=0$$
$$R:$$ $$u=-2x,$$ $$\,\,\,\,$$$$v=2y$$

Which flows should be recommended when the application requires the flow to be incompressible and irrotational?

Consider steady, incompressible and irrotational flow through a reducer in a horizontal pipe where the diameter is reduced from $$20cm$$ to $$10cm.$$ The pressure in the $$20cm$$ pipe just upstream of the reducer is $$150kPa.$$ The fluid has a vapour pressure of $$50kPa$$ and a specific weight of $$5\,\,kN/{m^3}.$$ Neglecting frictional effects, the maximum discharge (in $${m^3}/s$$) that can pass through the reducer without causing cavitation is

The velocity profile of a fully developed laminar flow in a straight circular pipe, as shown in the figure, is given by the expression. $$$u\left( r \right) = {{ - {R^2}} \over {4\mu }}\left( {{{dp} \over {dx}}} \right)\left( {1 - {{{r^2}} \over {{R^2}}}} \right)$$$
Where $${{dp} \over {dx}}$$ is a constant.

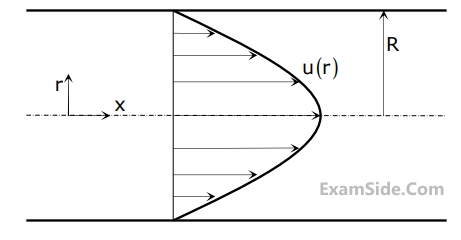
The average velocity of fluid in the pipe is

Consider steady-state heat conduction across the thickness in a plane composite wall as shown in fig exposed to convection conditions on both sides.

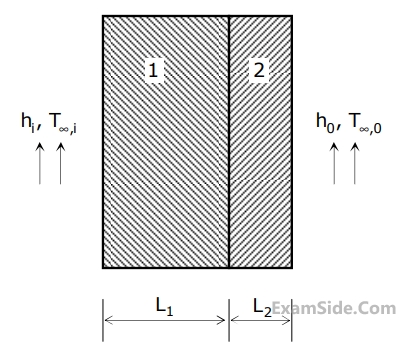
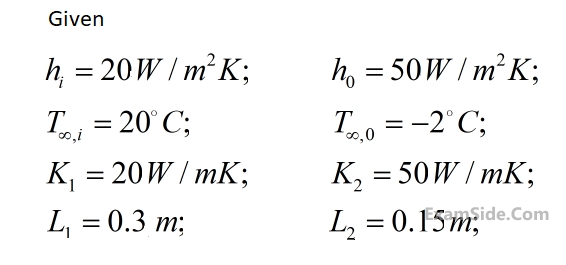
Assuming negligible contact resistance between the wall surfaces, the interface temp $$T(C)$$ of the two walls will be

A coolant fluid at $${30^ \circ }C$$ flows over a heated flat plate maintained at a constant temperature of $${100^ \circ }C$$. The boundary layer temp distribution at a given location on the plate may be approximated as $$T=30+70exp(-y),$$ where $$y$$ (in $$m$$) is the distance normal to the plate and $$T$$ is in $$^ \circ C.$$ If thermal conductivity of the fluid is $$1.0W/mk,$$ the local convective heat transfer (in $$W/{m^2}K$$) at that location will be

Radiative heat transfer is intended between the inner surfaces of two very largen isothermal parallel metal plates. While the upper plate (designated as plate $$1$$) is a black surface and is the warmer one being maintained at $${727^ \circ }C,$$ the lower plate (plate $$2$$) is a diffuse and gray surface with an emissivity of $$0.7$$ and is kept at $${27^ \circ }C.$$ Assume that the surfaces are sufficiently large to form a two-surface enclosure and steady state conditions to exist. Stefan Boltzmann constant is given as
$$5.67 \times {10^{ - 8}}\,W/{m^2}{K^4}$$

If plate is also a diffuse gray surface with an emisivity value of $$0.8,$$ the net radiant heat exchange (in $$kW/{m^2}$$) between plate $$1$$ and plate $$2$$

Radiative heat transfer is intended between the inner surfaces of two very largen isothermal parallel metal plates. While the upper plate (designated as plate $$1$$) is a black surface and is the warmer one being maintained at $${727^ \circ }C,$$ the lower plate (plate $$2$$) is a diffuse and gray surface with an emissivity of $$0.7$$ and is kept at $${27^ \circ }C.$$ Assume that the surfaces are sufficiently large to form a two-surface enclosure and steady state conditions to exist. Stefan Boltzmann constant is given as
$$5.67 \times {10^{ - 8}}\,W/{m^2}{K^4}$$

The irradiation (in $$kW/{m^2}$$) for the upper plate is

In a parallel flow heat exchanger operating under steady state, the heat capacity rates (product of specific heat at constant pressure and mass flow rate) of the hot and cold fluid are equal. The hot fluid, flowing at $$1kg/sec$$ with $$sp.$$ heat $$= 4kJ/kgK,$$ enters the heat exchanger at $${102^ \circ }C$$ while the cold fluid has an inlet temperature of $${15^ \circ }C$$. The overall heat transfer coefficient for the heat exchanger is estimated to be $$1\,\,kW/{m^2}K$$ and the corresponding heat transfer surface area is $$5{m^2}$$. Neglect heat transfer between the heat exchanger and the ambient.

The heat exchanger is characterized by the following relation $$2\varepsilon = 1 - Exp\left( { - 2NTU} \right).$$ The exit temp (in $$^ \circ C$$) for the cold fluid is

A company uses $$2555$$ units of an item annually. Delivery lead time is $$8$$ days. The recorder point (in number of units) to achieve optimum inventory is

The expected time $$\left( {{t_e}} \right)$$ of a $$PERT$$ activity in terms of optimistic time $$\left( {{t_0}} \right)$$, pessimistic $$\left( {{t_p}} \right)$$ and most likely time $$\left( {{t_L}} \right)$$ is given by

Consider the following network

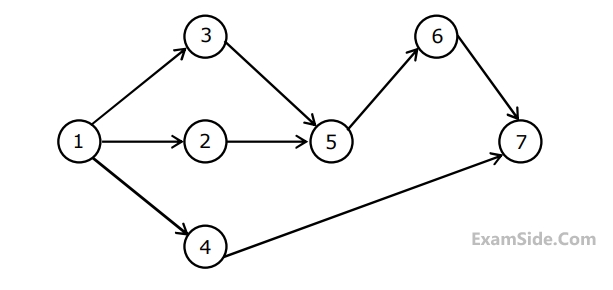
The optimistic time, most likely time and pessimistic time of all the activities are given in the table below :

The critical path duration of the network (in days) is

Consider the following network

The optimistic time, most likely time and pessimistic time of all the activities are given in the table below :

The standard deviation of the critical path is

Which of the following forecasting methods takes a fraction of forecast error into account for the next period forecast?

Consider the following Linear Programming problem $$(LLP)$$

Maximize: $$Z = 3{x_1} + 2{x_2}$$
$$\,\,$$ Subject $$\,\,$$ to
$$\eqalign{ & \,\,\,\,\,\,\,{x_1} \le 4 \cr & \,\,\,\,\,\,\,{x_2} \le 6 \cr & 3{x_1} + 2{x_2} \le 18 \cr & {x_1} \ge 0,\,\,{x_2} \ge 0 \cr} $$

Six jobs arrived in a sequence as given below:

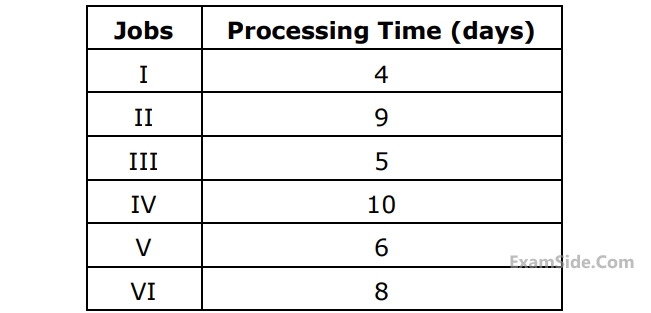
Average flow time (in days) for the above jobs using Shortest Processing Time rule is

A forged steel link with uniform diameter of $$30mm$$ at the centre is subjected to an axial force that varies from $$40kN$$ in compression to $$160kN$$ in tension. The tensile $$\left( {{S_U}} \right),$$ yield $$\left( {{S_y}} \right)$$ and corrected endurance $$\left( {{S_e}} \right)$$ strengths of the steel material are $$600MPa, 420MPa$$ and $$240MPa$$ respectively. The factor of safety against fatigue endurance as per Soderberg’s criterion is

A $${20^ \circ }$$ full depth involute spur pinion of $$4mm$$ module and $$21$$ teeth is to transmit $$15kW$$ at $$960rpm.$$ Its face width is $$25mm.$$

Given that the tooth geometry factor is $$0.32$$ and the combined effect of dynamic load and allied factors intensifying the stress is $$1.5;$$ the minimum allowable stress (in $$MPa$$) for the gear material is

A $${20^ \circ }$$ full depth involute spur pinion of $$4mm$$ module and $$21$$ teeth is to transmit $$15kW$$ at $$960rpm.$$ Its face width is $$25mm.$$

The tangential force transmitted (in N) is

Friction at the tool - chip interface can be reduced by

Two streams of liquid metal, which are not hot enough to fuse properly, result into a casting defect known as

Match the following

The minimum shear strain in orthogonal turning with a cutting tool of zero rake angle is

In a machining experiment, tool life was found to vary with the cutting speed in the following manner

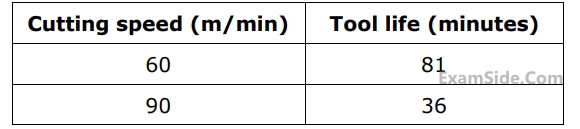
The exponent $$(n)$$ and constant $$(K)$$ of the Taylor's tool life equation are

In a machining experiment, tool life was found to vary with the cutting speed in the following manner

What is percentage increase in tool life when the cutting speed is halved.

What are the upper and lower limits of the shaft represented by $$60{f_8}$$?

Use the following data:
Diameter $$60$$ lies in the diameter step of $$50-80$$ $$mm$$
Fundamental tolerance unit, $$i,$$ in $$\mu m = 0.45\,\,{D^{1/3}} + 0.001D,$$
where $$D$$ is the representative size in $$mm;$$ Tolerance value for $${\rm I}T8 = 25i,$$ Fundamental deviation for $$'‘f’'$$ shaft $$ = - 5.5{D^{0.41}}$$

Match the following

If the principal stresses in a plane stress problem are $${\sigma _1}$$ $$= 100$$ MPa, $${\sigma _2}$$ $$= 40$$ MPa, the magnitude of the maximum shear stress (in MPa) wil be

A solid circular shaft of diameter $$d$$ is subjected to a combined bending moment, $$M$$ and torque, $$T.$$ The material property to be used for designing the shaft using the relation $${{16T} \over {\pi {d^3}}}\sqrt {{M^2} + {T^2}} $$

A solid shaft of diameter, $$d$$ and length, $$L$$ is fixed at both the ends. A torque, $${T_0}$$ is applied at a distance, $$L/4$$ from the left end as shown in the figure below.

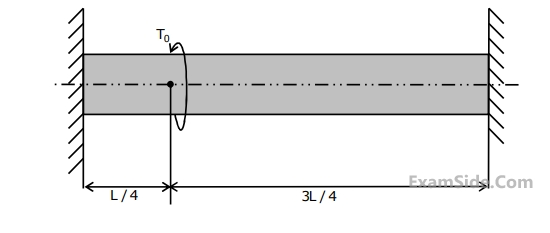
The maximum shear stress in the shaft is

A triangular-shaped cantilever beam of uniform- thickness is shown in the figure. The young's modulus of the material of the beam is $$E$$. $$A$$ concentrated load $$P$$ is applied at the free end of the beam.

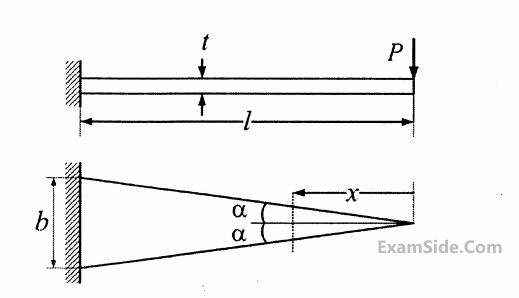
The area moment of inertia of inertia about the neutral axis of a cross-section at a distance $$x$$ measured from the free end is

A frame of two arms of equal length $$L$$ is shown in the adjacent figure. The flexural rigidity of each arm of the frame is $$EI$$. The vertical deflection at the point of application of load $$P$$ is

A triangular-shaped cantilever beam of uniform- thickness is shown in the figure. The young's modulus of the material of the beam is $$E$$. $$A$$ concentrated load $$P$$ is applied at the free end of the beam.

The maximum deflection of the beam is

A simple quick return mechanism is shown in the figure. The forward to return ratio of the quick return mechanism is 2 : 1. If the radius of the crank O₁ P is 125mm, then the distance 'd' (in mm) between the crank centre to lever pivot centre point should be

Match the approaches given below to perform stated kinematics/dynamics analysis of machine

Analysis
$$P.$$ Continuous relative rotation
$$Q.$$ Velocity and acceleration
$$R.$$ Mobility
$$S.$$ Dynamic - static analysis

Approach
$$1.$$ D' Alembert's principal
$$2.$$ Grubler's criterion
$$3.$$ Grashoff's law
$$4.$$ Kennedy's theorem

An epicyclic gear train is shown schematically in the adjacent figure The sun gear 2 on the input shaft is a 20 teeth external gear. The planet gear 3 is a 40 teeth external gear. The ring gear 5 is a 100 teeth internal gear. The ring gear 5 is fixed and the gear 2 is rotating at 60 rpm CCW (CCW $$=$$ counter-clockwise and CW $$=$$ clockwise)

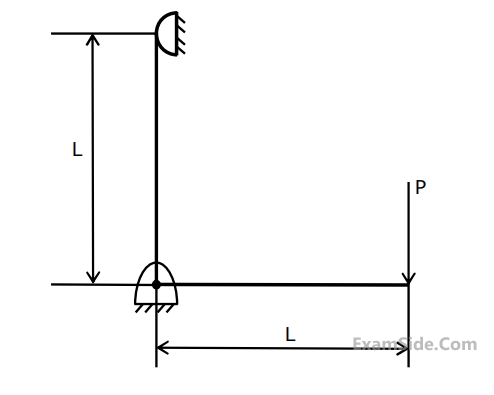
The arm 4 attached to the output shaft will rotate at

The rotor shaft of a large electric motor supported between short bearings at both the ends shows a deflection of $$1.8$$ mm in the middle of the rotor. Assuming the rotor to be perfectly balanced and supported at knife edges at both the ends, the likely critical speed (in rpm) of the shaft is

An automotive engine weighing $$240$$ kg is supported on four springs with linear characteristics. Each of the front two springs have a stiffness of $$16$$ MN/m while the stiffness of each rear spring is $$32$$ MN/m. The engine speed (in rpm), at which resonance is likely to occur, is

A vehicle suspension system consists of a spring and a damper. The stiffness of the spring is $$3.6$$ kN/m and the damping constant of the damper is $$400$$ Ns/m. If the mass is $$50$$ kg, then the damping factor ($$\xi $$) and damped natural frequency ($${f_n}$$) respectively are

A compressor undergoes a reversible, steady flow process. The gas at inlet and outlet of the compressor is designated as state $$1$$ and state $$2$$ respectively. Potential and kinetic energy changes are to be ignored. The following notations are used:
$$v=$$ specific volume and $$P=$$ pressure of the gas.
The specific work required to be supplied to the compressor for this gas compression process is

A frictionless piston-cylinder device contains a gas initially at $$0.8MPa$$ and $$0.015$$ $${m^3}.$$ It expands quasi-statically at constant temperature to a final volume of $$0.030$$ $${m^3}.$$ The work output (in $$kJ$$) during this process will be

If a closed system is undergoing an irreversible process, the entropy of the system

The inlet and the outlet conditions of steam for an adiabatic steam turbine are as indicated in the figure. The notations are as usually followed.

If mass flow rate of steam through the turbine is $$20kg/s,$$ the power output of the turbine (in $$MW$$) is

The inlet and the outlet conditions of steam for an adiabatic steam turbine are as indicated in the figure. The notations are as usually followed.

Assume the above turbine to be part of a simple Rankine cycle. The density of water at the inlet to the pump is $$1000$$ $$kg/{m^3}.$$ Ignoring kinetic and potential energy effects, the specific work (in $$kJ/kg$$) supplied to the pump is