GATE ME 2017 Set 1
GATE ME
1
The product of eigenvalues of the matrix $$P$$ is $$P = \left[ {\matrix{
2 & 0 & 1 \cr
4 & { - 3} & 3 \cr
0 & 2 & { - 1} \cr
} } \right]$$
2
The value of $$\mathop {\lim }\limits_{x \to 0} \left( {{{{x^3} - \sin \left( x \right)} \over x}} \right)$$ is
3
A parametric curve defined by $$x = \cos \left( {{{\pi u} \over 2}} \right),y = \sin \left( {{{\pi u} \over 2}} \right)\,\,$$ in the range $$0 \le u \le 1$$ is rotated about the $$x-$$axis by $$360$$ degrees. Area of the surface generated is
4
For the vector $$\overrightarrow V = 2yz\widehat i + 3xz\widehat j + 4xy\widehat k,$$ the value of $$\,\nabla .\left( {\nabla \times \overrightarrow \nabla } \right)\,\,$$ is ______________.
5
A six-face fair dice is rolled a large number of times. The mean value of the outcomes is _________.
6
The differential equation $$\,{{{d^2}y} \over {d{x^2}}} + 16y = 0$$ for $$y(x)$$ with the two boundary conditions $${\left. {{{dy} \over {dx}}} \right|_{x = 0}} = 1$$ and $${\left. {{{dy} \over {dx}}} \right|_{x = {\pi \over 2}}} = - 1$$ has
7
Consider the following partial differential equation for $$u(x,y)$$ with the constant $$c>1:$$ $$\,{{\partial u} \over {\partial y}} + c{{\partial u} \over {dx}} = 0\,\,$$ solution of this equation is
8
$$\,\,P\,\,\,\left( {0,3} \right),\,\,Q\,\,\,\left( {0.5,4} \right),\,\,$$ and $$\,\,R\,\,\,\left( {1,5} \right)\,\,\,$$ are three points on the curve defined by $$\,\,f\left( x \right),\,\,$$ Numerical integration is carried out using both Trapezoidal rule and Simpson's rule within limits $$x=0$$ and $$x=1$$ for the curve. The difference between the two results will be
9
The following figure shows the velocity- time plot for a particle traveling along a straight line. The distance covered by the particle from $$t = 0$$ to $$t= 5$$ $$s$$ is __________$$m.$$
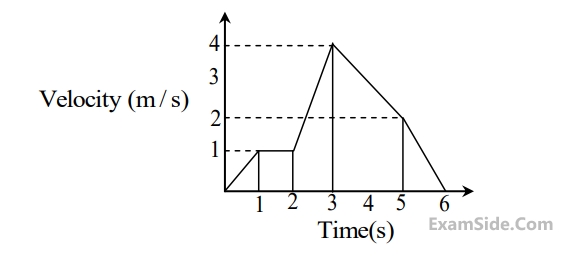

10
Two disks A and B with identical mass (m) and radius (R) are initially at rest. They roll down from the top of identical inclined planes without slipping. Disk A has all of its mass concentrated at the rim, while Disk B has its mass uniformly distributed. At the bottom of the plane, the ratio of velocity of the center of disk A to the velocity of the center of disk B is.
11
A Particle of unit mass is moving on a plane. Its trajectory, in polar coordinates, is given by $$r\left( t \right) = {t^2},\theta \left( t \right) = t,$$ where $$t$$ is time. The kinetic energy of the particle at time $$t=2$$ is
12
For a steady flow, the velocity field is $$\overrightarrow V = \left( { - {x^2} + 3y} \right)\widehat i + \left( {2xy} \right)\widehat j.$$ The magnitude of the acceleration of the particle at $$(1, -1)$$ is
13
For steady flow of a viscous incompressible fluid through a circular pipe of constant diameter, the average velocity in the fully developed region is constant. Which one of the following statements about the average velocity in the developing region is TRUE?
14
Consider steady flow of an incompressible fluid through two long and straight pipes of diameters $${d_1}$$ and $${d_2}$$ arranged in series. Both pipes are of equal length and the flow is turbulent in both pipes. The friction factor for turbulent flow though pipes is of the form, $$f = K{\left( {{\mathop{\rm Re}\nolimits} } \right)^{ - n}},$$ where $$K$$ and $$n$$ are known positive constants and $$Re$$ is the Reynolds number. Neglecting minor losses, the ratio of the frictional pressure drop in pipe $$1$$ to that in pipe $$2,$$ $$\left( {{{\Delta {P_1}} \over {\Delta {P_2}}}} \right),$$ is given by
15
The velocity profile inside the boundary layer for flow over a flat plate is given as $${u \over {{U_\infty }}} = \sin \left( {{\pi \over 2}\,{y \over \delta }} \right),$$ where $${U_\infty }$$ is the free stream velocity and $$'\delta '$$ is the local boundary layer thickness. If $${\delta ^ * }$$ is the local displacement thickness, the value of $${{{\delta ^ * }} \over \delta }$$ is
16
Consider the two-dimensional velocity field given by
$$\overrightarrow V = \left( {5 + {a_1}x + {b_1}y} \right)\widehat i + \left( {4 + {a_2}x + {b_2}y} \right)\widehat j,$$
where $${a_1},\,\,{b_1},\,\,{a_2}$$ and $${b^2}$$ are constants. Which one of the following conditions needs to be satisfied for the flow to be incompressible?
$$\overrightarrow V = \left( {5 + {a_1}x + {b_1}y} \right)\widehat i + \left( {4 + {a_2}x + {b_2}y} \right)\widehat j,$$
where $${a_1},\,\,{b_1},\,\,{a_2}$$ and $${b^2}$$ are constants. Which one of the following conditions needs to be satisfied for the flow to be incompressible?
17
Heat is generated uniformly in a long solid cylindrical rod ( diameter $$ = 10\,\,mm$$) at the rate of $$4 \times {10^7}\,\,W/{m^3}.$$ The thermal conductivity of the rod material is $$25$$ $$W/m.K.$$ Under steady state conditions, the temperature difference between the center and the surface of the rod is ________________ $${}^ \circ C.$$
18
Two black surfaces, $$AB$$ and $$BC,$$ of lengths $$5m$$ and $$6m,$$ respectively, are oriented as shown. Both surfaces extend infinitely into the third dimension. Given that view factor $${F_{12}} = 0.5,\,\,{T_1} = 800\,\,K,\,\,{T_2} = 600\,\,K,$$ $${T_{surrounding}} = 300\,\,K$$ and Stefan Boltzmann constant, $$\sigma = 5.67 \times {10^{ - 8}}\,\,W/\left( {{m^2}{K^4}} \right),$$ the heat transfer rate from Surface $$2$$ to the surrounding environment is ____________ $$kW.$$
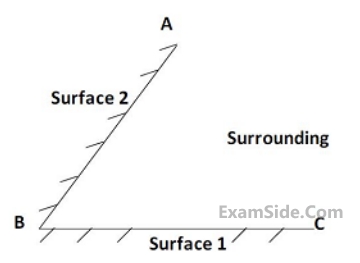

19
Saturated steam at $${100^ \circ }C$$ condenses on the outside of a tube. Cold fluid enters the tube at $${20^ \circ }C$$ and exits at $${50^ \circ }C.$$ The value of the Log Mean Temperature Difference $$(LMTD)$$ is _________ $$^ \circ C.$$
20
Two models, $$P$$ and $$Q,$$ of a product earn profits of Rs. $$100$$ and Rs. $$80$$ per piece, respectively. Production times for $$P$$ and $$Q$$ are $$5$$ hours and $$3$$ hours, respectively, while the total production time available is $$150$$ hours. For a total batch size of $$40,$$ to maximize profit, the number of units of $$P$$ to be produced is ____________.
21
Following data refers to the jobs $$(P, Q, R, S)$$ which have arrived at a machine for scheduling. The shortest possible average flow time is ___________ days.


22
Consider the schematic of a riveted lap joint subjected to tensile load $$F,$$ as shown below. Let $$d$$ be the diameter of the rivets, and $${S_f}$$ be the maximum permissible tensile stress in the plates. What should be the minimum value for the thickness of the plates to guard against tensile failure of the plates? Assume the plates to be identical.
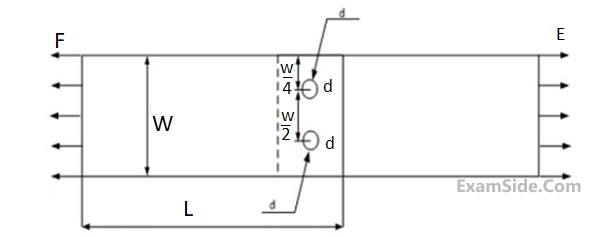

23
A machine element has an ultimate strength $$\left( {{\sigma _u}} \right)$$ of $$600\,\,N/m{m^2},$$ and endurance limit $$250$$ $$\,N/m{m^2}.$$ The fatigue curve for the element on log-log plot is shown below. If the element is to be designed for a finite of $$10000$$ cycles, the maximum amplitude of a completely reversed operating stress is _________ $$\,N/m{m^2}.$$
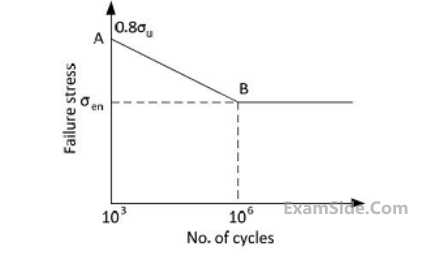

24
A sprue in a sand mould has a top diameter of $$20mm$$ and height of $$200mm.$$ The velocity of the molten metal at the entry of the sprue is $$0.5m/s.$$ Assume acceleration due to gravity as $$9.8\,\,m/{s^2}$$ and neglect all losses. If the mould is well ventilated, the velocity (upto $$3$$ decimal points accuracy) of the molten metal at the bottom of the sprue is ______________________ $$m/s.$$
25
In a metal forming operation when the material has just started yielding, the principal stresses are $${\sigma _1} = \,\, + 180\,\,MPa,\,\,\,$$ $${\sigma _2} = \,\, - 100\,\,MPa,\,\,\,$$ $${\sigma _3} = 0.$$ Following Von Mises' criterion, the yield stress is _____________ $$MPa.$$
26
In an arc welding process, welding speed is doubled. Assuming all other process parameters to be constant, the cross sectional area of the weld bead will
27
Two cutting tools with tool life equations given below are being compared:
$$\eqalign{ & Tool\,\,1:\,\,\,\,\,\,\,V{T^{0.1}} = 150 \cr & Tool\,\,2:\,\,\,\,\,\,\,V{T^{0.3}} = 300 \cr} $$
where $$V$$ is cutting speed in $$m/minute$$ and $$T$$ is tool life in minutes. The breakeven cutting speed beyond which Tool $$2$$ will have a higher tool life is _______________ $$m/minute$$.
$$\eqalign{ & Tool\,\,1:\,\,\,\,\,\,\,V{T^{0.1}} = 150 \cr & Tool\,\,2:\,\,\,\,\,\,\,V{T^{0.3}} = 300 \cr} $$
where $$V$$ is cutting speed in $$m/minute$$ and $$T$$ is tool life in minutes. The breakeven cutting speed beyond which Tool $$2$$ will have a higher tool life is _______________ $$m/minute$$.
28
Metric thread of $$0.8$$ $$mm$$ pitch is to be cut on a lathe. Pitch of the lead screw is $$1.5$$ $$mm.$$ If the spindle rotates at $$1500$$ $$rpm,$$ the speed of rotation of the lead screw $$(rpm)$$ will be _____________
29
A block of length $$200$$ $$mm$$ is machined by a slab milling cutter $$34$$ $$mm$$ in diameter. The depth of cut and table feed are set at $$2$$ $$mm$$ and $$18$$ $$mm/minute,$$ respectively. Considering the approach and the over travel of the cutter to be same, the minimum estimated machining time per pass is _____________ minutes.
30
A $$10$$ $$mm$$ deep cylindrical cup with diameter of $$15$$ $$mm$$ is drawn from a circular blank. Neglecting the variation in the sheet thickness, the diameter (upto $$2$$ decimal points accuracy) of the blank is _________ $$mm.$$
31
Cylindrical pins of diameter $${15^{ \pm 0.020}}\,\,mm$$ are being produced on a machine. Statistical quality control tests show a mean of $$14.995$$ $$mm$$ and standard deviation of $$0.004mm.$$ The process capability index $${C_p}$$ is
32
Assume that the surface roughness profile is triangular as shown schematically in the figure. If the peak to valley height is $$20$$ $$\mu m$$ The central line average surface roughness $${R_a}$$ (in $$\mu m$$) is


33
Circular arc on a part profile is being machined on a vertical $$CNC$$ milling machine. $$CNC$$ part program using metric units with absolute dimensions is listed below:
$$\eqalign{ & N60\,\,\,\,G01\,\,\,\,X\,30\,\,\,\,Y\,55\,\,\,\,Z\,5\,\,\,\,F50 \cr & N70\,\,\,\,G02\,\,\,X\,50\,\,\,\,Y\,35\,\,\,\,R\,20 \cr & N80\,\,\,\,G01\,\,\,\,Z\,5 \cr} $$
The coordinates of the center of the circular arc are:
34
In the engineering stress-strain curve for mild steel, the Ultimate Tensile Strength $$(UTS)$$ refers to
35
The Poisson's ratio for a perfectly incompressible linear elastic material is
36
A horizontal bar, fixed at one end (x = 0), has a length of 1 m, and cross-sectional area of 100 mm2. Its elastic modulus varies along its length as given by E(x) = 100 e-x GPa, Where x is the length coordinate (in m) along the axis of the bar. An axial tensile load of 10 kN is applied at the free end (x=1). The axial displacement of the free end is _______ mm.
37
A point mass of $$100$$ kg is dropped onto a massless elastic bar (cross-sectional area = $$100$$ $$mm$$2 ,length = $$1$$ m, Young's modulus = $$100$$ GPa) from a height $$H$$ of $$10$$ $$mm$$ as shown (Figure is not to scale). If g = $$10$$ $$m/s$$2 , the maximum compression of the elastic bar is _______ $$mm.$$
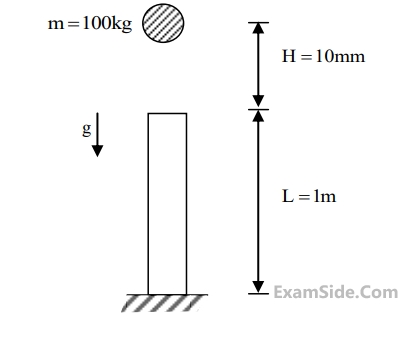

38
A rectangular region in a solid is in a state of plane strain. The $$(x,y)$$ coordinates of the corners of the undeformed rectangle are given by $$P(0,0), Q(4,0), R(4,3), S(0,3).$$ The rectangle is subjected to uniform strains, $${\varepsilon _{xx}} = 0.001,\,\,{\varepsilon _{yy}} = 0.002,\,\,{\gamma _{xy}} = 0.003.$$ The deformed length of the elongated diagonal, upto three decimal places, is ______________ units.
39
Consider a beam with circular cross-section of diameter $$d.$$ The ratio of the second moment of area about the neutral axis to the section modulus of the area is
40
A motor driving a solid circular steel shaft transmits $$40$$ $$kW$$ of power at $$500$$ $$rpm$$. If the diameter of the shaft is $$40$$ $$mm,$$ the maximum shear stress in the shaft is ________ $$MP$$a.
41
An initially stress-free massless elastic beam of length $$L$$ and circular cross-section with diameter $$d (d < < L)$$ is held fixed between two walls as shown. The beam material has Young's modulus $$E$$ and coefficient of thermal expansion $$\alpha .$$
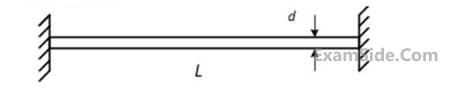

If the beam is slowly and uniformly heated, the temperature rise required to cause the beam to buckle is proportional to
42
For an inline slider-crank mechanism, the lengths of the crank and connecting rod are 3 m and 4 m respectively. At the instant when the connecting rod is perpendicular to the crank, if the velocity of the slider is 1 m/s, the magnitude of angular velocity (upto 3 decimal points accuracy) of the crank is _________ radian/s.
43
In an epicyclic gear train, shown in the figure, the outer ring gear is fixed, while the sun gear rotates counterclockwise at 100 rpm. Let the number of teeth on the sun, planet and outer gears to be 50, 25 and 100, respectively. The ratio of magnitudes of angular velocity of the planet gear to the angular velocity of the carrier arm is _________.
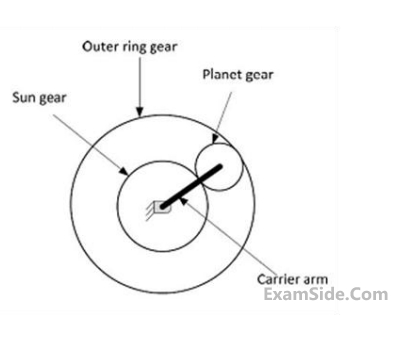

44
The damping ratio for a viscously damped spring mass system, governed by the relationship $$\,m{{{d^2}x} \over {d{t^2}}} + c{{dx} \over {dt}} + kx = f\left( t \right),\,\,\,$$ is given by
45
A thin uniform rigid bar of length $$L$$ and mass $$M$$ is hinged at point $$O,$$ located at a distance of $${L \over 3}$$ from one of its ends. The bar is further supported using springs, each of stiffness $$k,$$ located at the two ends. A particle of mass $$m = {m \over 4}$$ is fixed at one end of the bar, as shown in the figure. For small rotations of the bar about $$O,$$ the natural frequency of the systems is
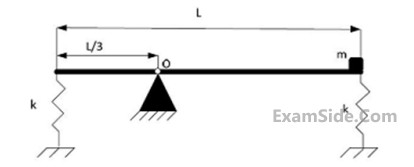

46
The molar specific heat at constant volume of an ideal gas is equal to $$2.5$$ times the universal gas constant ($$8.314$$ $$J/mol.K$$). When the temperature increases by $$100$$ $$K$$, the change in molar specific enthalpy is _______________ $$J/mol.$$
47
Water (density $$ = 1000$$ $$kg/{m^3}$$) at ambient temperature flows through a horizontal pipe of uniform cross section at the rate of $$1$$ $$kg/s.$$ If the pressure drop across the pipe is $$100$$ $$kPa,$$ the minimum power required to pump the water across the pipe, in watts, is
48
One $$kg$$ of an ideal gas (gas constant, $$R = 400$$ $$J/kg.K;$$ specific heat at constant volume, $${c_v} = 1000\,J/kg.K$$ at $$1$$ bar, and $$300$$ $$K$$ is contained in a sealed rigid cylinder. During an adiabatic process, $$100$$ $$kJ$$ of work is done on the system by a stirrer. The increase in entropy of the system is _________ $$J/K.$$
49
A heat pump absorbs $$10$$ $$kW$$ of heat from outside environment at $$250$$ $$K$$ while absorbing $$15$$ $$kW$$ of work. It delivers the heat to a room that must be kept warm at $$300$$ $$K.$$ The Coefficient of performance $$(COP)$$ of the heat pump is _____________.
50
Which one of the following is NOT a rotating machine?