A storm with a recorded precipitation of 11.0 cm, as shown in the table, produced a direct run-off of 6.0 cm.

Time from start (hours)	1	2	3	4	5	6	7	8
Recorded cumulative precipitation (cm)	0.5	1.5	3.1	5.5	7.3	8.9	10.2	11.0

The Ø-index of this storm is ______________ cm/hr (rounded off to 2 decimal places).

The ordinates of a 1-hour unit hydrograph (UH) are given below.

Time (hours)	0	1	2	3	4	5
Ordinates of 1-hour UH (m3/s)	0	13	50	80	95	85

Time (hours)	6	7	8	9	10	11
Ordinates of 1-hour UH (m3/s)	55	35	15	10	3	0

These ordinates are used to derive a 3-hour UH. The peak discharge (in m³/s) for the derived 3-hour UH is ___________ (rounded off to the nearest integer).

A catchment may be idealized as a circle of radius 30 km. There are five rain gauges, one at the center of the catchment and four on the boundary (equi-spaced), as shown in the figure (not to scale).

The annual rainfall recorded at these gauges in a particular year are given below.

$$ \begin{array}{|l|l|l|l|l|l|} \hline \text { Gauge } & \mathrm{G}_1 & \mathrm{G}_2 & \mathrm{G}_3 & \mathrm{G}_4 & \mathrm{G}_5 \\ \hline \text { Rainfall }(\mathrm{mm}) & 910 & 930 & 925 & 895 & 905 \\ \hline \end{array} $$

Using the Thiessen polygon method, what is the average rainfall (in mm, rounded off to two decimal places) over the catchment in that year? ________

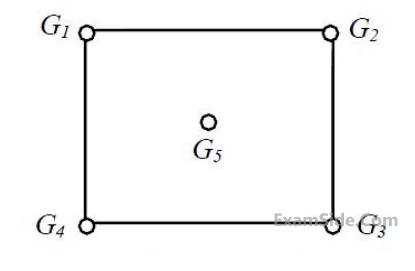A catchment is idealized as a 25 km × 25 km square. It has five rain gauges, one at each corner and one at the center, as shown in the figure. During a month, the precipitation at these gauges is measured as G₁ = 300 mm, G₂ = 285 mm, G₃ = 272 mm, G₄ = 290 mm and G₅ = 288 mm. The average precipitation (in mm, up to one decimal place) over the catchment during this month by using the Thiessen polygon method is_______ .