If $$\phi (x,y)$$ and $$\psi (x,y)$$ are function with continuous 2^nd derivatives then $$\phi (x,y)\, + \,i\psi (x,y)$$ can be expressed as an analytic function of x +iy ($$i = \sqrt { - 1} $$) when

A block of mass $$M$$ is related from point $$P$$ on a rough inclined plane with inclination angle $$\theta $$, shown in the figure below. The coefficient of friction is $$\mu $$. If $$\mu < \tan \theta $$, then the time taken by the block to reach anorher point $$Q$$ on the inclined plane, where $$PQ=S,$$ is

During inelastic collision of two particles, which one of the following is conserved?

Consider a steady incompressible flow through a channel as shown below.

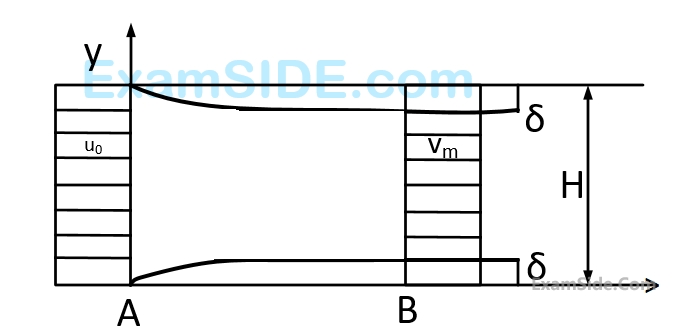
The velocity profile is uniform with a value of $${u_0}$$ at the inlet section $$A$$. The velocity profile at section B down stream is

$$$u\left\{ {\matrix{ {{V_m}{y \over \delta },} & {0 \le y \le \delta } \cr {{V_m},} & {\delta \le y \le H - \delta } \cr {{V_m}{{H - y} \over \delta },} & {H - \delta \le y \le H} \cr } } \right.$$$

The ratio $${{{V_m}} \over {{u_0}}}$$ is