Currents $${{\rm I}_1},\,{{\rm I}_2}$$ and $${{\rm I}_3}$$ meet at a junction (node) in a circuit. All currents are marked as entering the node. If $${{\rm I}_1} = - 6\sin \left( {\omega t} \right)$$ $$mA$$ and $${{\rm I}_2} = 8\cos \,\left( {\omega t} \right)\,mA,$$ then $${{\rm I}_3}$$ will be

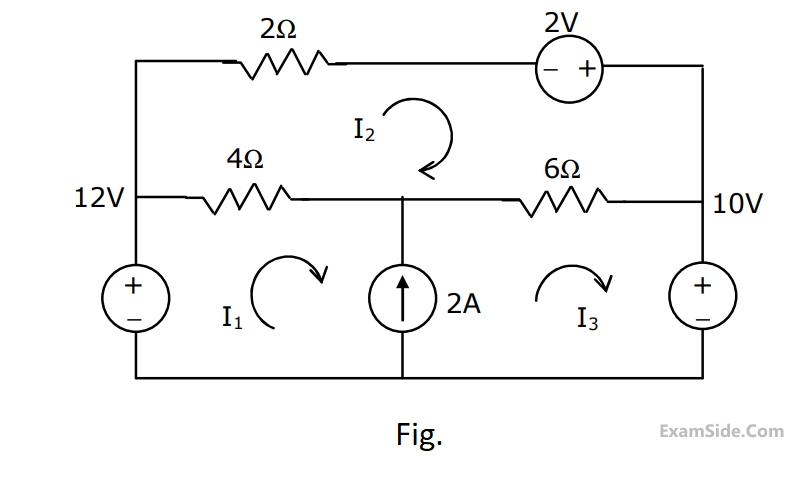
Solve the circuit shown in Fig. using the mesh method of analysis and determine the mesh currents $${{\rm I}_1},\,{{\rm I}_2},$$ and $${{\rm I}_3}$$. Evaluate the power developed in the $$10$$ $$V$$ voltage source.

A rectangular voltage pulse of magnitude $$V$$ and duration $$T$$ is applied to a series combination of resistance $$R$$ and capacitance $$C.$$ The maximum voltage developed across the capacitor is

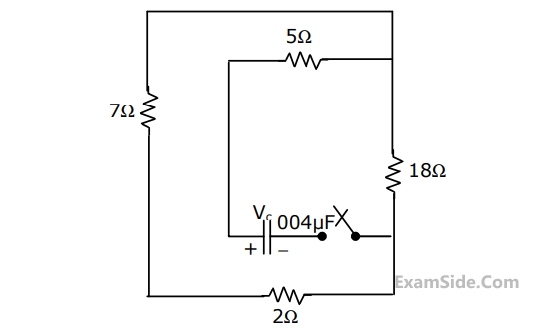
In the given circuit, the capacitor is initially charged to $$12$$ $$V. $$ Find the mathematical expression for the voltage across the capacitor $${{V_C}}$$ after closing the switch at $$t = 0.$$