Which from following compounds the thermocol is obtained?

Identify product A in following reaction.

$$ \mathrm{C}_6 \mathrm{H}_5 \stackrel{+}{\mathrm{N}}_2 \mathrm{Cl}^{-} \xrightarrow{\mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}} \mathrm{~A}+\mathrm{N}_2+\mathrm{CH}_3 \mathrm{CHO}+\mathrm{HCl} $$

Which among the following is vinylic halide?

Which of the following is Lewis base?

Which from following is a soft metal?

What is the order and molecularity respectively for the elementary reaction given below?

$$ \mathrm{O}_{3(\mathrm{~g})}+\mathrm{O}_{(\mathrm{g})} \longrightarrow 2 \mathrm{O}_{2(\mathrm{~g})} \text { if } \mathrm{r}=\mathrm{k}\left[\mathrm{O}_3\right][\mathrm{O}] $$

Identify the property of colloidal solutions so that colloidal particles move freely towards respective electrodes under an applied electrical potential.

Calculate the work done in following reaction at $27^{\circ} \mathrm{C}$.

$$ \begin{aligned} & 4 \mathrm{SO}_{2(\mathrm{~g})}+2 \mathrm{O}_{2(\mathrm{~g})} \longrightarrow 4 \mathrm{SO}_{3(\mathrm{~g})} \\ & \left(\mathrm{R}=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right) \end{aligned} $$

Which of the following principal of green chemistry suggest use of chemicals made from plant based sources?

Which from following cations will form most stable complex with same ligand?

Which is NOT correct regarding stock notation?

Calculate the time in seconds required to reduce the concentration of reactant to half of initial concentration for first order reaction if rate constant is $1.386 \times 10^{-3} \mathrm{~s}^{-1}$.

The solubility product of $\mathrm{PbI}_2$ is $1.08 \times 10^{-7}$.

Calculate its solubility in $\mathrm{mol} \mathrm{dm}^{-3}$ at 298 K .

If $\operatorname{Ln}$ represents lanthanoid element find the general formula of lanthanoid hydroxide.

Identify the correct decreasing order of boiling points for different organic compounds from following.

Which from following is a thermosetting polymer?

Which from following functional groups has highest priority order for naming the polyfunctional group compounds?

Identify the defect that develops when the ratio of number of cations to anions become different from that indicated by its chemical formula.

Which from following compounds does NOT contain phenolic - OH group?

Which of the following aqueous solutions exhibits lowest freezing point depression assuming complete dissociation?

Which of the following set of thermodynamic conditions is true for the reaction to be spontaneous at high temperature?

Calculate the energy per mole of photon of electromagnetic radiation having wavelength $700 \mathrm{~nm}\left[\mathrm{~h}=6.626 \times 10^{-34} \mathrm{Js}, \mathrm{c}=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right]$

Which of the following molecules consist minimum lone pair of electrons in the valence shell of central atom?

What is the SI unit of rate of diffusion for a gas?

Which of the following gases causes depletion in ozone layer?

Find standard enthalpy of formation of ammonia from following reaction.

$$ \mathrm{N}_{2(\mathrm{~g})}+3 \mathrm{H}_{2(\mathrm{~g})} \longrightarrow 2 \mathrm{NH}_{3(\mathrm{~g})} ; \Delta_{\mathrm{r}} \mathrm{H}^0=-92.0 \mathrm{~kJ} $$

What is IUPAC name of the following compound?

Which from the following reaction is a Fittig reaction?

What is IUPAC name of the following compound?

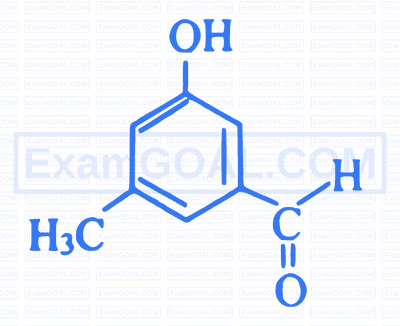
Which of the following compounds has highest boiling point?

Calculate the temperature of 0.05 M sucrose solution in Kelvin if the osmotic pressure of the solution is 1.5 atm .

$$ \left[\mathrm{R}=0.0821 \mathrm{dm}^3 \mathrm{~atm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right] $$

If $\mathrm{E}^*\left(\mathrm{Mg}^{+2}{ }_{(\mathrm{aq})} \mid \mathrm{Mg}_{(\mathrm{s})}\right)=-2.37 \mathrm{~V}$.

What is potential for $\mathrm{Mg}_{(\mathrm{s})} \rightarrow \mathrm{Mg}^{+2}(0.1 \mathrm{M})+2 \mathrm{e^-}$ at 298 K ?

Which of the following statements is false about interhalogen compounds?

The mass of an atom present in unit cell is $4.4 \times 10^{-23} \mathrm{~g}$ and the product of density and volume of unit cell is $1.792 \times 10^{-22} \mathrm{~g}$. What is the type of cubic unit cell?

Which amino acid from following is NOT synthesized in our body?

What is the coordination number of Pt in cisplatin?

What is the value of pH of a NaOH solution that dissociates $2 \%$ in its 0.01 M solution?

If standard emf of cell $\mathrm{Zn}_{(\mathrm{s})}\left|\mathrm{Zn}_{(\mathrm{iM})}^{+2}\right| \mathrm{Ag}_{(\mathrm{iM})}^{+1} \mid \mathrm{Ag}_{(\mathrm{s})}$ is 1.55 V .

What is electrical work done under standard conditions?

What is the number of chiral carbon atoms present in 3,4-Dibromohexane?

Identify the major product formed when 2-Methylhexan-3-ol is heated with concentrated sulphuric acid.

If a reaction occurs in following two steps

i. $2 \mathrm{ClO}^{-} \longrightarrow \mathrm{ClO}_2^{-}$

ii. $\mathrm{ClO}_2^{-}+\mathrm{ClO}^{-} \longrightarrow \mathrm{ClO}_3^{-}+\mathrm{Cl}^{-}$

Find the reaction intermediate.

Identify the product when magnesium burns in air.

Calculate the total number of tetrahedral and octahedral voids in 0.4 mol compound having such voids in it.

Which carbon atom of glucopyranose numbered from $\mathrm{C}-1$ to $\mathrm{C}-6$ is anomeric?

Calculate molality of the solution containing nonvolatile solute if boiling point elevation of the solution is 0.2 K

$$ \left[\mathrm{K}_{\mathrm{b}}=0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right] $$

Identify the reagent ' $R$ ' used in the following reaction.

Ketone $\xrightarrow{\mathrm{R}}$ Semicarbazone

Identify substrate ' $A$ ' in the following reaction.

$\mathrm{A}+\mathrm{CO}_2 \xrightarrow[6 \text { atm }]{398 \mathrm{~K}}$ Sodium salicylate $\xrightarrow{\mathrm{H}_3 \mathrm{O}^{+}}$Salicylic acid

If a random variable X follows the Binomial distribution $B(10, \quad p)$ such that $5 \mathrm{P}(\mathrm{X}=0)=\mathrm{P}(\mathrm{X}=1)$, then the value of $\frac{\mathrm{P}(\mathrm{X}=5)}{\mathrm{P}(\mathrm{X}=6)}$ is equal to

A particular solution of $\frac{\mathrm{d} y}{\mathrm{~d} x}=(x+9 y)^2$, when $x=0, y=\frac{1}{27}$ is

$$ \mathop {\lim }\limits_{x \to \infty } \frac{\mathrm{e}^{x^4}-1}{\mathrm{e}^{x^4}+1}= $$

The shortest distance between the lines $\bar{r}=(4 \hat{i}-\hat{j})+\lambda(\hat{i}+2 \hat{j}-3 \hat{k})$ and $\bar{r}=(\hat{i}-\hat{j}+2 \hat{k})+\mu(2 \hat{i}+4 \hat{j}-5 \hat{k})$ is

If $\mathrm{f}(x)=\cos (\log x)$ then $\mathrm{f}\left(x^2\right) \cdot \mathrm{f}\left(y^2\right)-\frac{1}{2}\left[\mathrm{f}\left(\frac{x^2}{y^2}\right)+\mathrm{f}\left(x^2 y^2\right)\right]$ has the value

The general solution of $\frac{\mathrm{d} y}{\mathrm{~d} x}=2 x y \mathrm{e}^{x^2}$ is

Which of the following is not a homogeneous function?

The maximum value and minimum value of the volume of the parallelopiped having coterminous edges $\hat{\mathrm{i}}+x \hat{\mathrm{j}}+\hat{\mathrm{k}}, \hat{\mathrm{j}}+x \hat{\mathrm{k}}$ and $x \hat{\mathrm{i}}+\hat{\mathrm{k}}$ are respectively

The following is the probability distribution of X

$$ \begin{array}{|c|c|c|c|c|} \hline \mathrm{X} & 0 & 1 & 2 & 3 \\ \hline \mathrm{P}(\mathrm{X}=x) & \frac{1+\mathrm{p}}{5} & \frac{2-2 \mathrm{p}}{5} & \frac{2-\mathrm{p}}{5} & \frac{2 \mathrm{p}}{5} \\ \hline \end{array} $$

$$ \text { For a minimum value of } p \text {, the value of } 5 E(X) \text { is } $$

Let $\overline{\mathrm{a}}$ and $\overline{\mathrm{c}}$ be unit vectors at an angle $\frac{\pi}{3}$ with each other. If $(\overline{\mathrm{a}} \times(\overline{\mathrm{b}} \times \overline{\mathrm{c}})) \cdot(\overline{\mathrm{a}} \times \overline{\mathrm{c}})=5$, then $[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]=$

A random variable X takes values $0,1,2,3$, ........ with probabilities. $\mathrm{P}(\mathrm{X}=x)=\mathrm{k}(x+1)\left(\frac{1}{2}\right)^x, \mathrm{k}$ is a constant, then $P(X=1)=$

The area inside the parabola $y^2=4 \mathrm{a} x$, between the lines $x=\mathrm{a}$ and $x=4 \mathrm{a}$ is equal to

$\int_2^4 \frac{\log x^2}{\log x^2+\log \left(36-12 x+x^2\right)} \mathrm{d} x$ is equal to

Let $\bar{a}, \bar{b}$, and $\bar{c}$ be unit vectors. Suppose that $\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}=\overline{\mathrm{a}} \cdot \overline{\mathrm{c}}=0$ and if the angle between $\overline{\mathrm{b}}$ and $\overline{\mathrm{c}}$ is $\frac{\pi}{6}$, then $\overline{\mathrm{a}}$ is

If $\overline{\mathrm{a}}$ and $\overline{\mathrm{b}}$ are unit vectors such that $|\overline{\mathrm{a}}+\overline{\mathrm{b}}|=\sqrt{3}$, then the angle between $\bar{a}$ and $\bar{b}$ is

The value of $\int_0^2\left[x^2\right] \mathrm{d} x$ is (where $[x]$ denotes the greatest integer function not greater than $x$ )

If $\quad \int \frac{3 \sin x \cos x}{4 \sin x+7} \mathrm{~d} x=\mathrm{A} \sin x-\mathrm{Blog}(4 \sin x+7)+\mathrm{c}$ where c is the constant of integration, then the value of $\mathrm{A}+\mathrm{B}$ is equal to

Three vectors $\hat{\mathrm{i}}-\hat{\mathrm{k}}, \lambda \hat{\mathrm{i}}+\hat{\mathrm{j}}+(1-\lambda) \hat{\mathrm{k}}$ and $\mu \hat{\mathrm{i}}+\lambda \hat{\mathrm{j}}+(1+\lambda-\mu) \hat{\mathrm{k}}$ represents coterminous edges of a parallelopiped, then the volume of the parallelopiped depends on.

$$ \int \frac{\mathrm{d} x}{x\left(x^2+1\right)}= $$

The joint equation of the bisectors of the angles between the lines $x=5$ and $y=3$ is

If $\sin ^{-1} \frac{1}{3}+\sin ^{-1} \frac{3}{5}+\sin ^{-1} x=\frac{\pi}{2}$ then $x=$

$\int \sqrt{x^2-6 x-16} \mathrm{~d} x$ equals

The value of $2 \tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{3}{8}$ is

With usual notation, in triangle ABC , $\mathrm{m} \angle \mathrm{A}=30^{\circ}$ then the value of $\left(1+\frac{\mathrm{a}}{\mathrm{c}}+\frac{\mathrm{b}}{\mathrm{c}}\right)\left(1+\frac{\mathrm{c}}{\mathrm{b}}-\frac{\mathrm{a}}{\mathrm{b}}\right)$ is equal to

The greatest possible number of points of intersection of 8 distinct straight lines and 4 distinct circles is

In $\triangle A B C$, with usual notations, $a \cos B=b \cos A, a \cos C \neq c \cos A$ then $\mathrm{A}(\triangle \mathrm{ABC})$ $\qquad$ sq. units.

The radius of the base of a cone is increasing at the rate $3 \mathrm{~cm} /$ minute and the altitude is decreasing at the rate $4 \mathrm{~cm} /$ minute . The rate at which the lateral surface area is changing, when the radius is 7 cm and altitude is 24 cm is

In a triangle ABC , with usual notations if $\mathrm{a}=4, \mathrm{~b}=8, \angle \mathrm{C}=60^{\circ}$, then the value of $\angle \mathrm{B}$ and the ratio $\cos \mathrm{A}: \cos \mathrm{C}$ respectively are,

The third element in the second row of adjoint of a matrix $A=\left[a_{i j}\right]_{3 \times 3}$ (where $a_{i j}=2 i+j$ ) is

The function f defined by $\mathrm{f}(x)=(x+2) \mathrm{e}^{-x}$ is

If the function $\mathrm{f}(x)=x(x+3) \mathrm{e}^{-\frac{x}{2}}$ satisfies all the conditions of Rolle's theorem in $[-3,0]$, then c is

If $(\mathrm{a}+\mathrm{b} x) \mathrm{e}^{\frac{y}{x}}=x$, then $x^3 \frac{\mathrm{~d}^2 y}{\mathrm{~d} x^2}$ is equal to

If $x=\log \mathrm{t}, \mathrm{t}>0$ and $y=\frac{1}{\mathrm{t}}$ then $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}=$

If $y=\frac{\mathrm{K}^{\cos ^{-1} x}}{1+\mathrm{K}^{\cos ^{-1} x}}$ and $\mathrm{t}=\mathrm{K}^{\cos ^{-1} x}$, then $\frac{\mathrm{d} y}{\mathrm{dt}}=$

The complex numbers $\sin x+i \cos 2 x$ and $\cos x$ - $\mathrm{i} \sin 2 x,(\mathrm{i}=\sqrt{-1})$ are conjugate to each other for,

The probability that in a random arrangement of the letters of the word 'UNIVERSITY', the two 'I's do not come together is

The logical statement

$$ [\sim(\sim p \vee q) \vee(p \wedge r) \wedge(\sim q \wedge r)] $$

is equivalent to

The L.P.P. , minimize $z=30 x+20 y, x+y \leq 8$, $x+2 y \geq 4,6 x+4 y \geq 12, x \geqslant 0, y \geqslant 0$ has

If the distance of the point $\mathrm{P}(1,-2,1)$ from the plane $x+2 y-2 z=\alpha$, where $\alpha>0$ is 5 units, then the foot of the perpendicular from P to the plane is

The equation of the plane containing the line $\frac{x-2}{3}=\frac{y+1}{2}=\frac{z-4}{-2}$ and the point $(0,5,0)$ is

If the statement pattern $(p \wedge q) \rightarrow(r \vee \sim s)$ is false, then the truth values of $p, q, r$ and $s$ are respectively

If $f(x)= \begin{cases}\frac{8^x-4^x-2^x+1}{x^2}, & \text { if } x>0 \\ e^x \sin x+x+\lambda \log 4, & \text { if } x \leqslant 0\end{cases}$

is continuous at $x=0$ then the value of $1000 \mathrm{e}^\lambda=$

The line of intersection of the planes $\bar{r} \cdot(3 \hat{i}-\hat{j}+\hat{k})=1 \quad$ and $\quad \bar{r} \cdot(\hat{i}+4 \hat{j}-2 \hat{k})=2 \quad$ is parallel to the vector

The Y-intercept of the common tangent to the parabolas $y^2=32 x$ and $x^2=108 y$ is

If the line $2 x+y=\mathrm{k}$ passes though the point which divides the line segment joining the points $(1,1)$ and $(2,4)$ internally in the ratio $3: 2$ then, $(k+1):(k-1)=$

The minimum distance and maximum distance of the point $\mathrm{P}(2,-7)$ from the circle $x^2+y^2-14 x-10 y-151=0$ are respectively _______units

The lines $\overline{\mathrm{r}}=\overline{\mathrm{a}}+\lambda(\overline{\mathrm{b}} \times \overline{\mathrm{c}})$ and $\overline{\mathrm{r}}=\overline{\mathrm{c}}+\lambda(\overline{\mathrm{a}} \times \overline{\mathrm{b}})$ will intersect if

$$ 3 \tan ^6 10^{\circ}-27 \tan ^4 10^{\circ}+33 \tan ^2 10^{\circ}= $$

The assets of a person reduced in his business such that the rate of reduction is proportional to the square root of the existing assets. If the assets were initially ₹ 10 lakhs and due to loss they reduce to ₹ 10000 after 3 years, then the number of years required for the person to be bankrupt will be

Two simple harmonic motions of angular frequency $300 \mathrm{rad} / \mathrm{s}$ and $3000 \mathrm{rad} / \mathrm{s}$ have same amplitude. The ratio of their maximum accelerations is

Two very long straight conductors (wires) are set parallel to each other. Each carries a current ' I ' in the same direction and the separation between them is ' 2 r '. The intensity of the magnetic field at point ' P ' (as shown in the figure) ( $\mu_0=$ permeability of free space) is

A rectangular block of surface area A emits energy E per second at $27^{\circ} \mathrm{C}$. If length and breadth is reduced to half of initial value and temperature is raised to $327^{\circ} \mathrm{C}$ then energy emitted per second becomes

A pipe open at both ends of length 1.5 m is dipped in water at one end such that $2^{\text {nd }}$ overtone of vibrating air column is resonating with a tuning fork of frequency 330 Hz . The length of the pipe immersed in water is (Speed of sound in air $=330 \mathrm{~m} / \mathrm{s}$ ) (Neglect end correction)

A physical quantity A can be determined by measuring parameters $\mathrm{B}, \mathrm{C}, \mathrm{D}$ and E using the relation $A=\frac{B^a C^\beta}{D^\gamma E^\delta}$. If the maximum errors in the measurement are $\mathrm{b} \%, \mathrm{c} \%, \mathrm{~d} \%$ and $\mathrm{e} \%$ then maximum error in the value of A is

In series LCR resonant circuit, R $=800 \Omega$, $\mathrm{C}=2 \mu \mathrm{~F}$ and voltage across resistance is 200 V . The angular frequency is $250 \mathrm{rad} / \mathrm{s}$. At resonance, the voltage across the inductance is

When a diatomic gas (rigid) undergoes adiabatic change, its pressure $(\mathrm{P})$ and temperature $(\mathrm{T})$ are related as $P \propto T^c$. The value of $c$ is

Two coils $P$ and $Q$ are kept near each other. When no current flows through coil $P$ and current increases in coil Q at the rate of $10 \mathrm{~A} / \mathrm{S}$, the e.m.f. in coil P is 15 mV . When coil Q carries no current and current of 1.8 A flows through coil $P$, the magnetic flux linked with coil Q is

A mass $m$ is suspended from a spring of negligible mass. The spring is pulled a little and then released, so that mass executes S.H.M. of time period $T$. If the mass is increased by $m_0$, the periodic time becomes $\frac{5 \mathrm{~T}}{4}$. The ratio $\frac{\mathrm{m}_0}{\mathrm{M}}$

The three vector $\vec{A}=3 \hat{i}-2 \hat{j}+\hat{k}, \vec{B}=\hat{i}-3 \hat{j}+5 k$ and $\vec{C}=2 \hat{i}-\hat{j}+4 \hat{k}$ will form

Two identical long parallel wires carry currents ' $\mathrm{I}_1$ ' and ' $\mathrm{I}_2$ ' such that $\mathrm{I}_1>\mathrm{I}_2$. When the currents are in the same direction, the magnetic field at a point midway between the wires is $8 \times 10^{-6} \mathrm{~T}$. If the direction of $\mathrm{I}_2$ is reversed, the field becomes $3.2 \times 10^{-5} \mathrm{~T}$. The ratio of $\mathrm{I}_2$ to $\mathrm{I}_1$ is

A disc of mass 25 kg and radius 0.2 m is rotating at 240 r.p.m. A retarding torque brings it to rest in 20 second. If the torque is due to a force applied tangentially on the rim of the disc then the magnitude of the force is

Interference fringes are produced on the screen by using two light sources of intensities I and 9I. The phase difference between the beams is $\pi / 2$ at point P and $\pi$ at point Q on the screen. The difference between the resultant intensities at points P and Q is $\left(\cos 90^{\circ}=0, \cos \pi=-1\right)$

Which of the following logic gates is called as Universal gate?

For an ideal gas, the density of the gas is $\rho_0$ when temperature and pressure of the gas are $\mathrm{T}_0$ and $P_0$ respectively. when the temperature of the gas is $2 \mathrm{~T}_0$, its pressure becomes $3 \mathrm{P}_0$. The new density will be

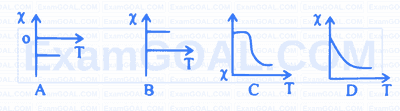
Which graph shows correctly the temperature (T). dependence of resistivity $(\rho)$ of a semiconductor?

Two uniform wires of same material are vibrating under the same tension. If the $1^{\text {st }}$ overtone of $1^{\text {st }}$ wire is equal to the $2^{\text {nd }}$ overtone of $2^{\text {nd }}$ wire and radius of $1^{\text {st }}$ wire is twice the radius of $2^{\text {nd }}$ wire, the ratio of length of $1^{\text {st }}$ wire to that $2^{\text {nd }}$ wire is

A liquid drop of volume V is placed on the surface of glass plate. Then another glass plate is placed on it such that liquid forms a thin layer of area A between the surfaces of two plates. To separate the plates a force F has to be applied normal to the surfaces. The surface tension of the liquid is

If maximum energy is stored in a capacitor at $\mathrm{t}=0$ then the time after which, current in the circuit will be maximum is

The velocity time graph of a body moving in a straight line is shown in figure. The ratio of displacement to distance travelled by the body in time 0 to 8 s is

The length of a potentiometer wire is ' $L$ ' . A cell of e.m.f. $E$ is balanced at a length $\frac{L}{5}$ from the positive end of the wire. If the length of the wire is increased by $\frac{L}{2}$, the same cell will give balance point at distance ' $x$ '. The value of ' $x$ ' is

In LCR series circuit, R = 18 $\Omega$ and impedance $33 \Omega$. An r.m.s. voltage of 220 V is applied across the circuit. The true power consumed in a.c. circuit is

A child stands on a weighing machine inside a lift. When the lift is going down with acceleration $\mathrm{g} / 3$, the machine shows a reading 20 N . When the lift goes upwards with acceleration $\mathrm{g} / 3$, the reading would be ( $\mathrm{g}=$ gravitational acceleration)

The equivalent capacitance between plates ' A ' and ' B ' ( A -area of each plate, d-separation between plates) ( $\varepsilon_0$ - permittivity of free space) is

Which of the following transitions in hydrogen atom emit photons of highest frequency? ( $\mathrm{n}=$ principle quantum number)

Water rises up to height ' $x$ ' in a capillary tube immersed vertically in water. When the whole arrangement is taken to a depth ' $d$ ' in a mine, the water level rises up to height Y . If R is the radius of the earth then the ratio $\mathrm{Y}: \mathrm{x}$ is

In Young's double slit experiment, in an interference pattern, a minimum is observed exactly in front of one slit. The distance between the two coherent sources is d and $\mathrm{D}_{\text { }}$ is the distance between source and screen. The possible wavelengths used are proportional to

The total energy of a circularly orbiting satellite is

The de-Broglie wavelength $(\lambda)$ of a particle

An incompressible fluid flows steadily through a cylindrical pipe having radius R at point A and $\left(\frac{\mathrm{R}}{3}\right)$ at point B further along the direction of flow of liquid. If the velocity at point A is ' V ' then that at point B is

Two radioactive materials $A$ and $B$ having decay constant ' $7 \lambda$ ' and ' $\lambda$ ' respectively, initially have same number of nuclei. The time taken to have the ratio of number of nuclei of material B to that of A as ' e ' is

A centigrade and Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit temperature observed is $140^{\circ} \mathrm{F}$. At that time the temperature registered by the centigrade thermometer is

Photoelectric emission is observed from a metallic surface for frequencies $v_1$ and $v_2$ of the incident light rays $\left(v_1>v_2\right)$. If the maximum values of kinetic energy of the photoelectrons emitted in the two cases are in the ratio of $1: \mathrm{k}$, then the threshold frequency of metallic surface is

The electric charges ' $+2 q$ ', ' $+2 q$ ', ' $-2 q$ ' and ' $-2 q$ ' are placed at the corners of square of side ' 2 L ' as shown in figure. The electric potential at point 'A', midway between the two charges ' $+2 q$ ' and ' $+2 q$ ' is

( $\varepsilon_0=$ permittivity of free space)

Two circular loops P and Q of radii ' r ' and ' nr ' are made respectively from a uniform wire. Moment of inertia of loop Q about its axis is 4 times that of loop $P$ about its axis. The value of $n$ is

An observer on sea-coast counts 45 waves in one minute. If the wavelength of the waves is 7 m , then the velocity of the waves will be

A simple pendulum has time period ' $\mathrm{T}_1$ '. The point of suspension is now moved upward according to equation $\mathrm{y}=\mathrm{kt}^2$ where $\mathrm{k}=1 \mathrm{~m} / \mathrm{s}^2$. If new time period is ' $\mathrm{T}_2$ ' then $\mathrm{T}_1^2 / \mathrm{T}_2^2$ will be ( $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )

To manufacture a solenoid of length ' $l$ ' and inductance ' $L$ ', the length of the thin wire required is (Diameter of the solenoid is very less than length, $\mu_0=$ permeability of free space)

An engine operating between temperatures $T_1$ and $T_2$ has efficiency $\frac{1}{5}$. When $T_2$ is lowered by 45 K , its efficiency becomes $\frac{1}{2}$. Temperatures $T_1$ and $T_2$ are respectively

In an n-p-n transistor amplifier, the collector current is 8 mA . If $80 \%$ of the electrons from the emitter reach the collector, then ( $\alpha$ and $\beta$ are current ratios)

An electric dipole having each charge of magnitude $2 \mu \mathrm{C}$ is placed in an electric field of intensity $8 \times 10^{+4} \mathrm{~N} / \mathrm{C}$. If the maximum torque acting on the dipole is $4 \times 10^{-3} \mathrm{~N}-\mathrm{m}$, the length of the dipole is

Two sources of sound are emitting progressive waves $\mathrm{y}_1=4 \sin 710 \pi \mathrm{t}$ and $\mathrm{y}_2=3 \sin 702 \pi \mathrm{t}$. The sources are placed close to each other. The number of beats heard per second and intensity ratio between waxing and waning are respectively

Three spheres, each of mass ' $m$ ' and radius ' $r$ ' are placed as shown in figure. Consider an axis $\mathrm{YY}^{\prime}$, which is touching two spheres and passing through the diameter of third sphere. The moment of inertia of the system consisting of these three spheres about $\mathrm{YY}^{\prime}$ axis is

$$ \text { The value of current I in the given circuit is } $$

Three polarised sheets are co-axially placed. Pass axis of polaroids 2 and 3 make $30^{\circ}$ and $90^{\circ}$ with pass axis of polaroid sheet. If $\mathrm{I}_0$ is the intensity of unpolarised light entering sheet 1 , the intensity of the emergent light through sheet 3 is

$$ \left(\cos 30^{\circ}=\sqrt{3} / 2, \cos 90^{\circ}=0, \cos 60^{\circ}=1 / 2\right) $$

Two cylinders A and B fitted with pistons contain equal amount of an ideal rigid diatomic gas at 303 K . The piston of cylinder $A$ is free to move and that of cylinder B is held fixed. The same amount heat is given to the gas in each cylinder. If the rise in temperature of the gas in cylinder B is 49 K , then the rise in temperature of the gas in $A$ is

The phenomenon, which is not due to total internal reflection is

Initially a rectangular coil with length vertical is moving out with constant velocity ' $v$ ' in a constant magnetic field ' $B$ ' towards right. Now the same coil is rotated through $90^{\circ}$ in same plane in same magnetic field B and the coil is moving with same velocity $\mathbf{v}$. The magnitude of induced e.m.f. is now

The voltage between the plates of a parallel plate capacitor of capacity $1 \mu \mathrm{~F}$ is changing at the rate of $4 \mathrm{~V} / \mathrm{s}$. the displacement current in the capacitor is