Identify cationic sphere complex from following.

Identify substrate '$$\mathrm{A}$$' in the following conversion.

$$\mathrm{A}+\underset{\text { (excess) }}{\mathrm{CH}_3 \mathrm{I}} \stackrel{\Delta}{\longrightarrow} {\mathrm{C}_2 \mathrm{H}_5}\left(\mathrm{CH}_3\right)_3 \stackrel{+}{\mathrm{N}} \mathrm{I}^{-}$$

Identify FALSE statement regarding adsorption from following.

Find the rate of formation of $$\mathrm{NO}_{2(\mathrm{~g})}$$ in the following reaction.

$$\begin{aligned} & 2 \mathrm{~N}_2 \mathrm{O}_{5(\mathrm{~g})} \rightarrow 4 \mathrm{NO}_{2(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})} \\ & {\left[\frac{-\mathrm{d}\left[\mathrm{N}_2 \mathrm{O}_5\right]}{\mathrm{dt}}=0.02 \mathrm{~mol} \mathrm{~dm}^{-3}\right]} \end{aligned}$$

Which from following properties is exhibited by group 2 elements?

Calculate the rate constant of the first order reaction if $$20 \%$$ of the reactant decomposes in 15 minutes.

Which from following methods of structural formula representation uses conventionally a point for front carbon and a circle around it for rear carbon?

Identify substrate '$$\mathrm{A}$$' in the following sequence of reactions.

A $$\mathrm{\mathrel{\mathop{\kern0pt\longrightarrow} \limits_\Delta ^{SOC{l_2}}}}$$ B $$\mathrm{\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{{C_2}{H_5}Cl}^{Na/ether}}}$$ 2-Methylbutane

Which of the following is tertiary benzylic alcohol?

Which among the following is a feature of $$\mathrm{S}_{\mathrm{N}} 1$$ mechanism?

The volume of a gas is $$4 \mathrm{~dm}^3$$ at $$0^{\circ} \mathrm{C}$$. Calculate new volume at constant pressure when the temperature is increased by $$10^{\circ} \mathrm{C}$$.

Which following reagent is used in Etard reaction?

Which of the following processes exhibits increase in internal energy?

Calculate $$\mathrm{E}_{\text {cell }}^0$$ if the equilibrium constant for following reaction is $$1.2 \times 10^6$$.

$$2 \mathrm{Cu}_{(\mathrm{aq})}^{+} \longrightarrow \mathrm{Cu}_{(\mathrm{aq})}^{++}+\mathrm{Cu}_{(\mathrm{s})}$$

Which from following alloys is used to make statues?

Which of the following molecules does NOT obey octet rule?

Calculate van't Hoff factor of $$\mathrm{K}_2 \mathrm{SO}_4$$ if $$0.1 \mathrm{~m}$$ aqueous solution of $$\mathrm{K}_2 \mathrm{SO}_4$$ freezes at $$-0.43{ }^{\circ} \mathrm{C}$$ and cryoscopic constant of water is $$1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$$.

Find the radius of fourth orbit of hydrogen atom if its radius of first orbit is $$\mathrm{R}$$ pm.

Which noble gas element from following exhibits highest number of different oxidation states?

Which among the following is a pair of monocarboxylic acids?

Identify the overall oxidation reaction that occurs in lead storage cell during discharge.

What is the change in oxidation number of selenium in the following redox reaction?

$$\mathrm{SeO}_{3(\text { (a) })}^{2-}+\mathrm{Cl}_{2(\mathrm{~g})}+2 \mathrm{OH}^{-} \longrightarrow \mathrm{SeO}_{4(\text { (a) })}^{2-}+2 \mathrm{Cl}_{(\text {(a) })}^{-}+\mathrm{H}_2 \mathrm{O}$$

A buffer solution is prepared by mixing equimolar acetic acid and sodium acetate. If '$$\mathrm{K}_d$$' of acetic acid is $$1.78 \times 10^{-5}$$, find the $$\mathrm{pH}$$ of buffer solution.

What is the number of moles of nascent hydrogen required to prepare 1 mole of methane from iodomethane?

Which from following metal has hcp crystal structure?

One mole of an ideal gas performs $$900 \mathrm{~J}$$ of work on surrounding. If internal energy increases by $$625 \mathrm{~J}$$, find the value of $$\Delta \mathrm{H}$$.

Which of the following temperature values in Fahrenheit $$\left({ }^{\circ} \mathrm{F}\right)$$ is equal to $$50^{\circ} \mathrm{C}$$ ?

Which from following formulae is of trioxalatocobaltate(III) ion?

Which of the following pair of nuclides is an example of isotones?

Identify FALSE statement from following.

What is IUPAC name of crotonyl alcohol?

A solution of $$5.6 \mathrm{~g}$$ non-volatile solute in $$50 \mathrm{~g}$$ solvent has elevation in boiling point $$1.75 \mathrm{~K}$$. What is the molar mass of solute $$\left(\mathrm{K}_{\mathrm{b}}=3 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right)$$ ?

What is the common name of benzene-1,3-diol?

Identify the CORRECT decreasing order of basic strength of compounds from following.

Calculate the work done in the following reaction at $$300 \mathrm{~K}$$ and at constant pressure.

$$\left(\mathrm{R}=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)$$

$$4 \mathrm{HCl}_{(\mathrm{g})}+\mathrm{O}_{2(\mathrm{~g})} \rightarrow 2 \mathrm{Cl}_{2(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{g})}$$

The solubility product of $$\mathrm{Mg}(\mathrm{OH})_2$$ is $$1.8 \times 10^{-11}$$ at $$298 \mathrm{~K}$$. What is its solubility in $$\mathrm{mol} \mathrm{~dm}^{-3}$$ ?

If $$\mathrm{K}_{\mathrm{sp}}$$ is solubility product of $$\mathrm{Al}(\mathrm{OH})_3$$, its solubility is expressed by formula,

Which from following is the slope of the graph of $$[\mathrm{A}]_{\mathrm{t}}$$ versus time for zero order reaction?

Which from following statements is NOT true about natural rubber?

What is the molal elevation constant if one gram mole of a nonvolatile solute is dissolved in $$1 \mathrm{~kg}$$ of ethyl acetate? $$\left(\Delta \mathrm{T}_{\mathrm{b}}=x \mathrm{~K}\right)$$

Which from following elements exhibits ferromagnetic properties?

Which of the following is NOT a globular protein?

Calculate the time required in second to deposit $$6.35 \mathrm{~g}$$ copper from its salt solution by passing 5 ampere current. [Molar mass of $$\mathrm{Cu}=63.5 \mathrm{~g} \mathrm{~mol}^{-1}$$ ]

Which from following nanomaterial has one dimension less than $$100 \mathrm{~nm}$$ ?

Which among the following compounds has highest boiling point?

Calculate the radius of metal atom in bcc unit cell having edge length $$287 \mathrm{~pm}$$.

Identify A in the following reaction.

$$\mathrm{{C_6}{H_{12}}{O_6}\mathrel{\mathop{\kern0pt\longrightarrow} \limits_{dil.\,HN{O_3}}^{(O)}} A}$$

Which of the following is formed when propene is heated with chlorine at high temperature?

Identify the monomer used to prepare Teflon.

Calculate the number of atoms present in unit cell if an element having molar mass $$23 \mathrm{~g} \mathrm{~mol}^{-1}$$ and density $$0.96 \mathrm{~g} \mathrm{~cm}^{-3}$$.

$$[\mathrm{a}^3 \cdot \mathrm{N}_{\mathrm{A}}=48 \mathrm{~cm}^3 \mathrm{~mol}^{-1}]$$

If $$\mathrm{f}(x)=x^3+\mathrm{b} x^2+\mathrm{c} x+\mathrm{d}$$ and $$0<\mathrm{b}^2<\mathrm{c}$$, then in $$(-\infty, \infty)$$

Differentiation of $$\tan ^{-1}\left(\frac{\sqrt{1+x^2}-1}{x}\right)$$ w.r.t. $$\cos ^{-1}\left(\sqrt{\frac{1+\sqrt{1+x^2}}{2 \sqrt{1+x^2}}}\right)$$ is

The function $$\mathrm{f}(\mathrm{t})=\frac{1}{\mathrm{t}^2+\mathrm{t}-2}$$ where $$\mathrm{t}=\frac{1}{x-1}$$ is discontinuous at

A random variable $$X$$ has the following probability distribution

then P(X < 2) is

If $$\mathrm{I}=\int \frac{2 x-7}{\sqrt{3 x-2}} \mathrm{~d} x$$, then $$\mathrm{I}$$ is given by

Let $$\mathrm{X}$$ be random variable having Binomial distribution $$B(7, p)$$. If $$P[X=3]=5 P[X=4]$$, then variance of $$\mathrm{X}$$ is

The scalar product of vectors $$\overline{\mathrm{a}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}$$ and a unit vector along the sum of vectors $$\bar{b}=2 \hat{i}-4 \hat{j}+5 \hat{k}$$ and $$\bar{c}=\lambda \hat{i}+2 \hat{j}-3 \hat{k}$$ is one, then the value of $$\lambda$$ is

$$\int \frac{\log \left(x^2+a^2\right)}{x^2} d x=$$

The parametric equations of the curve $$x^2+y^2+a x+b y=0$$ are

The sides of a triangle are three consecutive natural numbers and its largest angle is twice the smallest one, then the sides of the triangle (in units) are

$$x, y, z$$ are in G.P. and $$\tan ^{-1} x, \tan ^{-1} y, \tan ^{-1} z$$ are in A.P., then

In $$\triangle A B C$$ with usual notation, $$\frac{\cos A}{a}=\frac{\cos B}{b}=\frac{\cos C}{c}$$ and $$a=\frac{1}{\sqrt{6}}$$, then the area of triangle is _______ sq. units.

If $$\hat{\mathrm{a}}$$ and $$\hat{\mathrm{b}}$$ are unit vectors and $$\overline{\mathrm{c}}=\hat{\mathrm{b}}-(\hat{\mathrm{a}} \times \overline{\mathrm{c}})$$, then minimum value of $$[\hat{a} \hat{b} \bar{c}]$$ is

Angles of a triangle are in the ratio $$4: 1: 1$$. Then the ratio of its greatest side to its perimeter is

If a continuous random variable $$\mathrm{X}$$ has probability density function $$\mathrm{f}(x)$$ given by

$$f(x)=\left\{\begin{array}{cl} a x & , \text { if } 0 \leq x<1 \\ a & , \text { if } 1 \leq x<2 \\ 3 a-a x & , \text { if } 2 \leq x \leq 3 \\ 0 & , \text { otherwise } \end{array}\right.$$,

then a has the value

The value of $$\begin{aligned} \cos \left(18^{\circ}-\mathrm{A}\right) \cdot \cos ( & \left.18^{\circ}+\mathrm{A}\right) \\ & -\cos \left(72^{\circ}-\mathrm{A}\right) \cos \left(72^{\circ}+\mathrm{A}\right) \text { is }\end{aligned}$$

If $$\int x^5 e^{-4 x^3} \mathrm{~d} x=\frac{1}{48} \mathrm{e}^{-4 x^3} \mathrm{f}(x)+\mathrm{c}$$, where $$\mathrm{c}$$ is a constant of integration, then $$\mathrm{f}(x)$$ is given by

The solution of the differential equation $$\mathrm{e}^{-x}(y+1) \mathrm{d} y+\left(\cos ^2 x-\sin 2 x\right) y \mathrm{~d} x=0$$ at $$x=0$$, $$y=1$$ is

If $$A=\left[\begin{array}{ccc}1 & 2 & 3 \\ -1 & 1 & 2 \\ 1 & 2 & 4\end{array}\right]$$ and $$A_{i j}$$ is a cofactor of $$a_{i j}$$ then the value of $$a_{21} A_{21}+a_{22} A_{22}+a_{23} A_{23}$$ is

Rate of increase of bacteria in a culture is proportional to the number of bacteria present at that instant and it is found that the number doubles in 6 hours. The number of bacteria becomes ________ times at the end of 18 hours.

The slope of the normal to the curve $$x=\sqrt{t}$$ and $$y=t-\frac{1}{\sqrt{t}}$$ at $$t=4$$ is

If $$3 \mathrm{f}(x)-\mathrm{f}\left(\frac{1}{x}\right)=8 \log _2 x^3, x>0$$, then $$\mathrm{f}(2), \mathrm{f}(4)$$, $$f(8)$$ are in

If the angle between the lines given by $$x^2-3 x y+\lambda y^2+3 x-5 y+2=0 ; \lambda \geq 0$$ is $$\tan ^{-1}\left(\frac{1}{3}\right)$$, then the value of $$\lambda$$ is

A line drawn from the point $$\mathrm{A}(1,3,2)$$ parallel to the line $$\frac{x}{2}=\frac{y}{4}=\frac{z}{1}$$, intersects the plane $$3 x+y+2 z=5$$ in point $$\mathrm{B}$$, then co-ordinates of point $$\mathrm{B}$$ are

The value of $$\frac{\mathrm{i}^{248}+\mathrm{i}^{246}+\mathrm{i}^{244}+\mathrm{i}^{242}+\mathrm{i}^{240}}{\mathrm{i}^{249}+\mathrm{i}^{247}+\mathrm{i}^{245}+\mathrm{i}^{243}+\mathrm{i}^{241}}, (\mathrm{i}=\sqrt{-1})$$ is

If $$\mathrm{f}(x)=\int \frac{x^2 \mathrm{~d} x}{\left(1+x^2\right)\left(1+\sqrt{1+x^2}\right)}$$ and $$\mathrm{f}(0)=0$$, then $$\mathrm{f}(1)$$ is

A line $$\mathrm{L}_1$$ passes through the point, whose p. v. (position vector) $$3 \hat{i}$$, is parallel to the vector $$-\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}$$. Another line $$\mathrm{L}_2$$ passes through the point having p.v. $$\hat{i}+\hat{j}$$ is parallel to vector $$\hat{i}+\hat{k}$$, then the point of intersection of lines $$L_1$$ and $$L_2$$ has p.v.

If $$y=\tan ^{-1}\left(\frac{4 \sin 2 x}{\cos 2 x-6 \sin ^2 x}\right)$$, then $$\left(\frac{\mathrm{d} y}{\mathrm{~d} x}\right)$$ at $$x=0$$ is

The expression $$(p \wedge \sim q) \vee q \vee(\sim p \wedge q)$$ is equivalent to

The raw data $$x_1, x_2, \ldots \ldots, x_{\mathrm{n}}$$ is an A.P. with common difference $$\mathrm{d}$$ and first term $$0, \bar{x}$$ and $$\sigma^2$$ are mean and variance of $$x_{\mathrm{i}}, \mathrm{i}=1,2, \ldots \ldots \mathrm{n}$$, then $$\sigma^2$$ is

The particular solution of differential equation $$\mathrm{e}^{\frac{d y}{d x}}=(x+1), y(0)=3$$ is

A card is drawn at random from a well shuffled pack of 52 cards. The probability that it is black card or face card is

If $$\bar{a}=2 \hat{i}+3 \hat{j}-4 \hat{k}$$ and $$\bar{b}=\hat{i}-\hat{j}-\hat{k}$$, then the projection of $$\bar{b}$$ in the direction of $$\bar{a}$$ is

If $$\mathrm{f}(x)=\left\{\begin{array}{ll}\mathrm{e}^{\cos x} \sin x & , \text { for }|x| \leq 2 \\ 2, & \text { otherwise }\end{array}\right.$$, then $$\int_\limits{-2}^3 \mathrm{f}(x) \mathrm{d} x$$ is equal to

The equation of the line passing through the point $$(-1,3,-2)$$ and perpendicular to each of the lines $$\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$$ and $$\frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}$$ is

Let $$\mathrm{f}: \mathrm{R} \rightarrow \mathrm{R}$$ be a function such that $$\mathrm{f}(x)=x^3+x^2 \mathrm{f}^{\prime}(1)+x \mathrm{f}^{\prime \prime}(2)+6, x \in \mathrm{R}$$, then $$\mathrm{f}(2)$$ is

If $$A(1,4,2)$$ and $$C(5,-7,1)$$ are two vertices of triangle $$A B C$$ and $$G\left(\frac{4}{3}, 0, \frac{-2}{3}\right)$$ is centroid of the triangle $$A B C$$, then the mid point of side $$B C$$ is

The base of an equilateral triangle is represented by the equation $$2 x-y-1=0$$ and its vertex is $$(1,2)$$, then the length (in units) of the side of the triangle is

Five persons $$\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$$ and $$\mathrm{E}$$ are seated in a circular arrangement. If each of them is given a cap of one of the three colours red, blue and green, then the number of ways of distributing the caps such that the persons seated in adjacent seats get different coloured caps, is

The distance of the point $$(-1,-5,-10)$$ from the point of intersection of the line $$\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{12}$$ and the plane $$x-y+z=5$$ is

Negation of inverse of the following statement pattern $$(p \wedge q) \rightarrow(p \vee \sim q)$$ is

If $$\mathrm{f}(x)=3 x^{10}-7 x^8+5 x^6-21 x^3+3 x^2-7$$, then $$\lim _\limits{\alpha \rightarrow 0} \frac{f(1-\alpha)-f(1)}{\alpha^3+3 \alpha}=$$

The area (in sq. units) of the region bounded by curves $$y=3 x+1, y=4 x+1$$ and $$x=3$$ is

Values of $$c$$ as per Rolle's theorem for $$f(x)=\sin x+\cos x+6$$ on $$[0,2 \pi]$$ are

A vector $$\bar{a}$$ has components 1 and $$2 p$$ with respect to a rectangular Cartesian system. This system is rotated through a certain angle about origin in the counter clock wise sense. If, with respect to the new system, $$\bar{a}$$ has components 1 and $$(p+1)$$, then

A line is drawn through the point $$(1,2)$$ to meet the co-ordinate axes at $$\mathrm{P}$$ and $$\mathrm{Q}$$ such that it forms a $$\triangle \mathrm{OPQ}$$, where $$\mathrm{O}$$ is the origin. If the area of $$\triangle \mathrm{OPQ}$$ is least, then the slope of the line $$\mathrm{PQ}$$ is

If feasible region is as shown in the figure, then related inequalities are

The general solution of the equation $$3 \sec ^2 \theta=2 \operatorname{cosec} \theta$$ is

A right circular cone has height $$9 \mathrm{~cm}$$ and radius of base $$5 \mathrm{~cm}$$. It is inverted and water is poured into it. If at any instant, the water level rises at the rate $$\frac{\pi}{\mathrm{A}} \mathrm{cm} / \mathrm{sec}$$. where $$\mathrm{A}$$ is area of the water surface at that instant, then cone is completely filled in

If $$\theta$$ is angle between the vectors $$\bar{a}$$ and $$\bar{b}$$ where $$|\bar{a}|=4,|\bar{b}|=3$$ and $$\theta \in\left(\frac{\pi}{4}, \frac{\pi}{3}\right)$$, then $$|(\bar{a}-\bar{b}) \times(\bar{a}+\bar{b})|^2+4(\bar{a} \cdot \bar{b})^2$$ has the value

Select the 'WRONG' statement out of the following.

Two cells $$E_1$$ and $$E_2$$ having equal EMF '$$E$$' and internal resistances $$r_1$$ and $$r_2\left(r_1>r_2\right)$$ respectively are connected in series. This combination is connected to an external resistance '$$R$$'. It is observed that the potential difference across the cell $$\mathrm{E}_1$$ becomes zero. The value of '$$R$$' will be

Which one of the following represents correctly the variation of volume (V) of an ideal gas with temperature $$(\mathrm{T})$$ under constant pressure conditions?

Using variation of force and time given below, final velocity of a particle of mass $$2 \mathrm{~kg}$$ moving with initial velocity $$6 \mathrm{~m} / \mathrm{s}$$ will be

$$\mathrm{dQ}$$ is the heat energy supplied to an ideal gas under isochoric conditions. If $$\mathrm{dU}$$ and $$\mathrm{dW}$$ denote the change in internal energy and the work done respectively then

A black body at temperature $$127^{\circ} \mathrm{C}$$ radiates heat at the rate of $$5 \mathrm{~cal} / \mathrm{cm}^2 \mathrm{~s}$$. At a temperature $$927^{\circ} \mathrm{C}$$, its rate of emission in units of $$\mathrm{cal} / \mathrm{cm}^2 \mathrm{~s}$$ will be

The following graph represents

A rigid body rotates with an angular momentum L. If its rotational kinetic energy is made four times, its angular momentum will become

A radioactive sample has half-life of 5 years. The percentage of fraction decayed in 10 years will be

Three coils of inductance $$\mathrm{L}_1=2 \mathrm{H}, \mathrm{L}_2=3 \mathrm{H}$$ and $$\mathrm{L}_3=6 \mathrm{H}$$ are connected such that they are separated from each other. To obtain the effective inductance of 1 henry, out of the following combinations as shown in figure, the correct one is

A Carnot engine has the same efficiency between (i) $$100 \mathrm{~K}$$ and $$600 \mathrm{~K}$$ and (ii) $$\mathrm{T} \mathrm{K}$$ and $$960 \mathrm{~K}$$. The temperature $$\mathrm{T}$$ in kelvin of the sink is

For which of the following substances, the magnetic susceptibility is independent of temperature?

When a light of wavelength $$300 \mathrm{~nm}$$ fall on a photoelectric emitter, photo electrons are emitted. For another emitter light of wavelength $$600 \mathrm{~nm}$$ is just sufficient for liberating photoelectrons. The ratio of the work function of the two emitters is

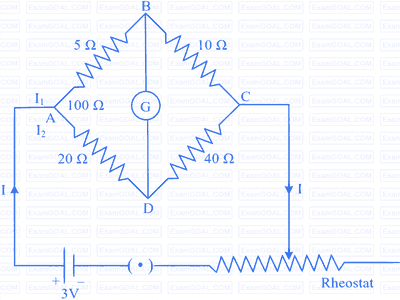
In a given meter bridge, the current flowing through $$40 \Omega$$ resistor is

A body of mass $$0.04 \mathrm{~kg}$$ executes simple harmonic motion (SHM) about $$\mathrm{x}=0$$ under the influence of force $$\mathrm{F}$$ as shown in graph. The period of

A large number of water droplets each of radius '$$t$$' combine to form a large drop of Radius '$$R$$'. If the surface tension of water is '$$T$$' & mechanical equivalent of heat is '$$\mathrm{J}$$' then the rise in temperature due to this is

In resonance tube, first and second resonance are obtained at depths $$22.7 \mathrm{~cm}$$ and $$70.2 \mathrm{~cm}$$ respectively. The third resonance will be obtained at a depth

Twenty seven droplets of water each of radius $$0.1 \mathrm{~mm}$$ merge to form a single drop then the energy released is

If two inputs of a NAND gate are shorted, the resulting gate is

Venturimeter is used to

Which of the following statements is 'WRONG' for the conductors?

A circular coil of radius '$$r$$' and number of turns ' $n$ ' carries a current '$$I$$'. The magnetic fields at a small distance '$$h$$' along the axis of the coil $$\left(B_a\right)$$ and at the centre of the coil $$\left(\mathrm{B}_{\mathrm{c}}\right)$$ are measured. The relation between $$B_c$$ and $$B_a$$ is

A spherical surface of radius of curvature '$$R$$' separates air from glass of refractive index 1.5. The centre of curvature is in the glass. A point object $$\mathrm{P}$$ placed in air forms a real image $$\mathrm{Q}$$ in the glass. The line $$P Q$$ cuts the surface at point '$$O$$' and $$\mathrm{PO}=\mathrm{OQ}=\mathrm{x}$$. Hence the distance '$$\mathrm{x}$$' is equal to

The rotational kinetic energy and translational kinetic energy of a rolling body are same, the body is

Two concentric circular coils A and B have radii $$20 \mathrm{~cm}$$ and $$10 \mathrm{~cm}$$ respectively lie in the same plane. The current in coil A is $$0.5 \mathrm{~A}$$ in anticlockwise direction. The current in coil B so that net field at the common centre is zero, is

A charged spherical conductor of radius '$$R$$' is connected momentarily to another uncharged spherical conductor of radius '$$r$$' by means of a thin conducting wire, then the ratio of the surface charge density of the first to the second conductor is

The magnet is moved towards the coil with speed '$$\mathrm{V}$$'. The induced e.m.f. in the coil is '$$\mathrm{e}$$'. The magnet and the coil move away from one another each moving with speed '$$\mathrm{V}$$'. The induced e.m.f. in the coil is

A uniform wire $$20 \mathrm{~m}$$ long and weighing $$50 \mathrm{~N}$$ hangs vertically. The speed of the wave at mid point of the wire is (acceleration due to gravity $$=\mathrm{g}=10 \mathrm{~ms}^{-2}$$ )

A large number of bullets are fired in all directions with same speed '$$U$$'. The maximum area on the ground on which the bullets will spread is

A transformer has 20 turns in the primary and 100 turns in the secondary coil. An ac voltage of $$\mathrm{V}_{\text {in }}=600 \sin 314 \mathrm{t}$$ is applied to primary terminal of transformer. Then maximum value of secondary output voltage obtained in volt is

On increasing the reverse bias to a large value in a P-N junction diode, current

For an ideal gas the density of the gas is $$\rho_0$$ when temperature and pressure of the gas are $$T_0$$ and $$P_0$$ respectively. When the temperature of the gas is $$2 \mathrm{~T}_0$$, its pressure will be $$3 \mathrm{P}_0$$. The new density will be

The temperature gradient in a rod of length $$75 \mathrm{~cm}$$ is $$40^{\circ} \mathrm{C} / \mathrm{m}$$. If the temperature of cooler end of the rod is $$10^{\circ} \mathrm{C}$$, then the temperature of hotter end is

In an oscillating LC circuit, the maximum charge on the capacitor is '$$Q$$'. When the energy is stored equally between the electric and magnetic fields, the charge on the capacitor becomes

A body of mass '$$\mathrm{m}$$' is raised through a height above the earth's surface so that the increase in potential energy is $$\frac{\mathrm{mgR}}{5}$$. The height to which the body is raised is ( $$\mathrm{R}=$$ radius of earth, $$\mathrm{g}=$$ acceleration due to gravity)

With increase in frequency of a.c. supply, the impedance of an L-C-R series circuit

A passenger is sitting in a train which is moving fast. The engine of the train blows a whistle of frequency '$$n$$'. If the apparent frequency of sound heard by the passenger is '$$f$$' then

If the magnitude of intensity of electric field at a distance '$$r_1$$' on an axial line and at a distance '$$r_2$$' on an equatorial line due to a given short dipole are equal, then $$r_1: r_2$$, is

In an a.c. circuit the instantaneous current and emf are represented as $$\mathrm{I}=\mathrm{I}_0, \sin [\omega \mathrm{t}-\pi / 6]$$ and $$\mathrm{E}=\mathrm{E}_0 \sin [\omega \mathrm{t}+\pi / 3]$$ respectively. The voltage leads the current by

In a biprism experiment, monochromatic light of wavelength '$$\lambda$$' is used. The distance between two coherent sources '$$\mathrm{d}$$' is kept constant. If the distance between slit and eyepiece '$$\mathrm{D}$$' is varied as $$D_1, D_2, D_3 \& D_4$$ and corresponding measured fringe widths are $$Z_1, Z_2, Z_3$$ and $$Z_4$$ then

Three charges each of value $$+q$$ are placed at the corners of an isosceles triangle $$\mathrm{ABC}$$ of sides $$\mathrm{AB}$$ and $$\mathrm{AC}$$ each equal to $$2 \mathrm{a}$$. The mid points of $$A B$$ and $$A C$$ are $$D$$ and $$E$$ respectively. The work done in taking a charge $$Q$$ from $$D$$ to $$E$$ is ( $$\varepsilon_0=$$ permittivity of free space)

Light of frequency 1.5 times the threshold frequency is incident on photosensitive material. If the frequency is halved and intensity is doubled, the photocurrent becomes

A solid cylinder of mass $$3 \mathrm{~kg}$$ is rolling on a horizontal surface with velocity $$4 \mathrm{~m} / \mathrm{s}$$. It collides with a horizontal spring whose one end is fixed to rigid support. The force constant of material of spring is $$200 \mathrm{~N} / \mathrm{m}$$. The maximum compression produced in the spring will be (assume collision between cylinder & spring be elastic)

Which one of the following statements is Wrong?

The fundamental frequency of a sonometer wir carrying a block of mass '$$M$$' and density '$$\rho$$' is '$$n$$' Hz. When the block is completely immerse in a liquid of density '$$\sigma$$' then the new frequency will be

A simple pendulum has a time period '$$T$$' in air. Its time period when it is completely immersed in a liquid of density one eighth the density of the material of bob is

Array of light is incident at an angle of incidence '$$i$$' on one surface of a prism of small angle $$\mathrm{A}$$ and emerges normally from the other surface. If the refractive index of the material of the prism is '$$\mu$$', then the angle of incidence is equal to

An isotope of the original nucleus can be formed in a radioactive decay, with the emission of following particles.

If two identical spherical bodies of same material and dimensions are kept in contact, the gravitational force between them is proportional to $$\mathrm{R}^{\mathrm{X}}$$, where $$\mathrm{x}$$ is non zero integer [Given : $$\mathrm{R}$$ is radius of each spherical body]

$$\mathrm{A}$$ and $$\mathrm{B}$$ are two interfering sources where $$\mathrm{A}$$ is ahead in phase by $$54^{\circ}$$ relative to B. The observation is taken from point $$\mathrm{P}$$ such that PB $$-$$ PA = 2.5 $$\lambda$$. Then the phase difference between the waves from A and B reaching point P is (in rad)