$$ \text { What is IUPAC name of following compound? } $$

What is the value of $K_{s p}$ for saturated solution of $\mathrm{Ba}(\mathrm{OH})_2$ having pH 12 ?

Benzonitrile on reduction with stannous chloride in presence of hydrochloric acid followed by acid hydrolysis forms,

Identify from following salts so that the solubility of salt in water decreases with increase in temperature.

Which from following polymers is obtained by condensation polymerisation method?

For a Galvanic cell consisting zinc electrode and standard hydrogen electrode,

$$ \mathrm{E}^{\mathrm{o}}\left(\mathrm{Zn}_{(\mathrm{aq})}^{+2} \mid \mathrm{Zn}_{(\mathrm{s})}\right)=-0.76 \mathrm{~V} $$

Identify the reaction that takes place at positive electrode during working of cell?

Which from following polymers is classified as fibre?

Which from following is a correct representation of reaction rate for reaction stated below?

$$ \mathrm{N}_{2(\mathrm{~g})}+3 \mathrm{H}_{2(\mathrm{~g})} \rightleftharpoons 2 \mathrm{NH}_{3(\mathrm{~g})} $$

Which of the following methods is used to prepare dihydrogen with purity greater than 99.5 ?

Cyclohexene on oxidation with $\mathrm{KMnO}_4$ in dil. $\mathrm{H}_2 \mathrm{SO}_4$ forms

Calculate the enthalpy change of vaporisation of benzene if 13 gram of benzene vaporised by supplying 5.1 kJ of heat.

The volume of simple unit cell is $x \times 10^{-23} \mathrm{~cm}^3$. Calculate the value of $x$ if volume occupied by a particle in it is $2.1 \times 10^{-23} \mathrm{~cm}^3$.

What is IUPAC name of the following compound?

What is the pH of buffer solution prepared by mixing 0.01 M weak acid and 0.02 M salt of weak acid with strong base? $\left(\mathrm{pK}_{\mathrm{a}}=4.680\right)$

Calculate the entropy change of surrounding if 2 moles of $\mathrm{H}_2$ and 1 mole of $\mathrm{O}_2$ gas combine to form 2 moles of liquid water by releasing 525 kJ heat to surrounding at constant pressure and at 300 K .

$$ \text { Identify the bond line formula of Neopentane. } $$

What is the number of faraday required to form $1 \mathrm{~mol} \mathrm{H}_2$ by reduction of $\mathrm{H}^{+}$ions?

Identify the name of method used for three dimensional representation of molecule as follows.

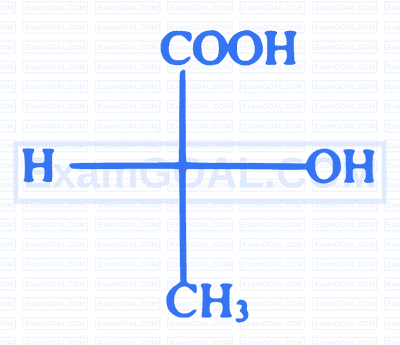
Identify the correct molecular formula of 'Oleum' from following.

Which of the following is a redox reaction?

Identify the product ' B ' in the following sequence of reactions.

Methyl magnesium bromide $\xrightarrow{\mathrm{CdCl}_2} \mathrm{~A}\xrightarrow{\mathrm{CH}_3 \mathrm{COCl}} \mathrm{~B}$

What is the number of $>\mathrm{C}=\mathrm{C}<$ bonds present in a linolenic acid molecule?

Which among the following is an allylic halide?

When tert butyl bromide is heated with silver fluoride the major product obtained is

Calculate the molal elevation constant of solvent if boiling point of 0.12 m solution is 319.8 K (Boling point of solvent $=319.5 \mathrm{~K}$ )

Which from following pairs of carbohydrates produce equal quantity of glucose on hydrolysis per mole?

Which of the following molecules has a regular geometry as expected?

What is the loss in molar mass when a primary amine is obtained by Hofmann degradation of amide?

Which from following is true according to Gay-Lussac's law?

Identify example of sorption from following.

Which from following carbohydrates produces double quantity of glucose on hydrolysis per mole as compared with sucrose?

In ionic solid, anions are arranged in ccp array and cations occupy $1 / 3$ tetrahedral voids. What is the formula of ionic compound?

[Consider $\mathrm{A}=$ cation; $\mathrm{B}=$ anion]

Which of the following is NOT dihydric phenol?

Calculate the concentration of an aqueous solution of non electrolyte at 300 K if its osmotic pressure is 12 atm .

$$ \left[\mathrm{R}=0.0821 \mathrm{~atm} \mathrm{dm}^3 \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right] $$

Which from following compounds is least soluble in water at STP?

Which of the following statements is correct about $\mathrm{O}_2$ and $\mathrm{O}_3$ molecule?

What is the total number of donor atoms present in Tetracyanonickelate(II) ion?

Half life of a first order reaction is 900 minute at 400 K , find its half life at 300 K ?

$$ \left(\frac{\mathrm{E}_{\mathrm{a}}}{2.303 \mathrm{R}}=1.3056 \times 10^3\right) $$

Which solvent from following is used in order to avoid creation of waste and pollution of air?

For the cell,

${ }^{\ominus} \mathrm{Zn}_{(\mathrm{s})}\left|\mathrm{Zn}^{+2}(1 \mathrm{M})\right|\left|\mathrm{Ag}^{+1}(1 \mathrm{M})\right| \mathrm{Ag}_{(\mathrm{s})}{ }^{\oplus}$

If concentration of $\mathrm{Zn}^{+2}$ decreases to 0.1 M at 298 K , then emf of cell

Identify the product ' B ' in the following series of reactions.

Which of the following statements is NOT correct regarding voids in lattice structure?

Identify pair of complexes that exhibits solvate isomerism.

Identify the element from following such that the last electron is placed in $(\mathrm{n}-1) \mathrm{d}$ orbital.

Which transition series includes elements Co and Mo respectively?

Rate law for the reaction,

$$ \mathrm{C}_2 \mathrm{H}_5 \mathrm{I}_{(\mathrm{g})} \longrightarrow \mathrm{C}_2 \mathrm{H}_{4(\mathrm{~g})}+\mathrm{HI}_{(\mathrm{g})} \text { is } \mathrm{r}=\mathrm{k}\left[\mathrm{C}_2 \mathrm{H}_5 \mathrm{I}\right] $$

What is the order and molecularity of this reaction?

Find the mass of potassium chlorate required to liberate $5.6 \mathrm{dm}^3$ of oxygen gas at STP? (molar mass of $\mathrm{KClO}_3=122.5 \mathrm{~g} / \mathrm{mol}$ )

Which of the following reactions exhibits decrease in entropy?

What is the wavenumber of the photon emitted during transition from the orbit $\mathrm{n}=5$ to that of $\mathrm{n}=2$ in hydrogen atom? $\left[\mathrm{R}_{\mathrm{H}}=109677 \mathrm{~cm}^{-1}\right]$

If pH of solution changes from 4 to 5 , then the $\mathrm{H}_3 \mathrm{O}^{+}$ion concentration of solution

The last column in the truth table of the statement pattern $[\mathrm{p} \rightarrow(\mathrm{q} \wedge \sim \mathrm{p})] \vee[(\mathrm{p} \vee \sim \mathrm{q}) \wedge \mathrm{p}]$ is

A straight line through the origin $O$ meets the line $3 y=10-4 x$ and $8 x+6 y+5=0$ at the points $A$ and B respectively. Then O divides the segment $A B$ in the ratio

The position of a point in time $t$ is given by $x=\mathrm{a}+\mathrm{bt}-\mathrm{ct}^2, y=\mathrm{at}+\mathrm{bt}^2$. It's resultant acceleration at time $t$ in seconds is given by

Let $\overline{\mathrm{OA}}=\overline{\mathrm{a}}, \overline{\mathrm{OB}}=\overline{\mathrm{b}}$ and if the vector along the angle bisector of $\angle \mathrm{AOB}$ is given by $x \frac{\overline{\mathrm{a}}}{|\overline{\mathrm{a}}|}+y \frac{\overline{\mathrm{~b}}}{|\overline{\mathrm{~b}}|}$ then

In triangle ABC , the point P divides BC internally in the ratio $3: 4$ and Q divides CA internally in the ratio $5: 3$. If AP and BQ intersect in a point $G$, then $G$ divides $A P$ internally in the ratio

The derivative of

$$ y=(1-x)(2-x) \ldots \ldots \ldots \ldots \ldots \ldots(\mathrm{n}-x) $$

at $x=1$ is

If $X \sim B(n, p)$ then $\frac{P(X=k)}{P(X=k-1)}=$

The differential equation of all straight lines passing through the point $(1,-1)$ is

The first derivative of the function $\left(\cos ^{-1}\left(\sin \sqrt{\frac{1+x}{2}}\right)+x^x\right)$ with respect to $x$ at $x=1$ is

Let $\bar{u}, \bar{v}, \bar{w}$ be the vectors such that $|\overline{\mathrm{u}}|=1,|\overline{\mathrm{v}}|=2,|\overline{\mathrm{w}}|=3$. If the projection $\overline{\mathrm{v}}$ along $\overline{\mathrm{u}}$ is equal to that of $\overline{\mathrm{w}}$ along $\overline{\mathrm{u}}$ and the vectors $\overline{\mathrm{v}}, \overline{\mathrm{w}}$ are perpendicular to each other then $|\overline{\mathrm{u}}-\overline{\mathrm{v}}+\overline{\mathrm{w}}|$ equals

The area enclosed between the curves $y^2=4 x$ and $y=|x|$ is

If $\tan \mathrm{A}=\frac{1}{\sqrt{x\left(x^2+x+1\right)}}, \tan \mathrm{B}=\frac{\sqrt{x}}{\sqrt{x^2+x+1}}$ and $\tan \mathrm{C}=\sqrt{x^{-1}+x^{-2}+x^{-3}}$ then

Let X be a discrete random variable. The probability distribution of X is given below

$$ \begin{array}{|c|c|c|c|} \hline \mathrm{X} & 30 & 10 & -10 \\ \hline \mathrm{P}(\mathrm{X}) & \frac{1}{5} & \mathrm{~A} & \mathrm{~B} \\ \hline \end{array} $$

and $\mathrm{E}(\mathrm{X})=4$, then the value of AB is equal to

The projection of the line segment joining the points $(2,1,-3)$ and $(-1,0,2)$ on the line whose direction ratios are $3,2,6$ is

If $x^{\frac{2}{5}}+y^{\frac{2}{5}}=\mathrm{a}^{\frac{2}{5}}$ then $\frac{\mathrm{d} y}{\mathrm{~d} x}=$

$$ \begin{aligned} &\text { The value of }\\ &\begin{aligned} \sin ^{-1}\left(-\frac{1}{\sqrt{2}}\right)+\cos ^{-1} & \left(-\frac{1}{2}\right) -\cot ^{-1}\left(-\frac{1}{\sqrt{3}}\right)+\tan ^{-1}(-\sqrt{3}) \text { is } \end{aligned} \end{aligned} $$

If triangle ABC is a right angled at A and $\tan \frac{\mathrm{B}}{2}$, $\tan \frac{\mathrm{C}}{2}$ are roots of the equation $a x^2+b x+c=0$, $\mathrm{a} \neq 0$, then

If $a^2+b^2+c^2=r^2$, then the value of $\tan ^{-1}\left(\frac{\mathrm{ab}}{\mathrm{cr}}\right)+\tan ^{-1}\left(\frac{\mathrm{bc}}{\mathrm{ar}}\right)+\tan ^{-1}\left(\frac{\mathrm{ca}}{\mathrm{br}}\right)=$

The feasible region for the constraints $x-2 \leqslant y, x \geqslant y-1, x \geqslant 2, y \leqslant 4, x, y \geqslant 0$, is _________

A plane passes through $(2,1,2)$ and $(1,2,1)$ and parallel to the line $2 x=3 y$ and $\mathrm{z}=1$, then the plane also passes through the point

In a game, 3 coins are tossed. A person is paid $Rs \, 150$ if he gets all heads or all tails and he is supposed to pay ₹50 if he gets one head or two heads. The amount he can expect to win / lose on an average per game in ₹ is

If $\sin \left(\sin ^{-1} \frac{1}{5}+\cos ^{-1} x\right)=1$, then the value of $x$ is

If two sides of a triangle are $\sqrt{3}-2$ and $\sqrt{3}+2$ units and their included angle is $60^{\circ}$, then the third side of the triangle is

The principal increases continuously in a newly opened bank at the rate of $10 \%$ per year. An amount of Rs. 2000 is deposited with this bank. How much will it become after 5 years?

$$ \left(\mathrm{e}^{0.5}=1.648\right) $$

If $A=\left[\begin{array}{rr}1 & 2 \\ -1 & 4\end{array}\right]$ and $A^{-1}=\alpha I+\beta A \alpha, \beta \in R$ where I is the identity matrix of order 2 , then $4(\alpha+\beta)=$

The solution of $\frac{\mathrm{d} y}{\mathrm{~d} x}=(x+y)^2$ is

A normal is drawn at a point $\mathrm{P}(x, y)$ of a curve $y=\mathrm{f}(x)$. The normal meets the $X$ axis at $Q$. $l(\mathrm{PQ})=\mathrm{k} \cdot(\mathrm{k}$ is a constant) Then equation of the curve through $(0, k)$ is

If $\mathrm{f}(x)=\frac{(27-2 x)^{\frac{1}{3}}-3}{9-3(243+5 x)^{\frac{1}{5}}}, x \neq 0$ is continuous at $x=0$, then the value of $\mathrm{f}(0)$ is

$$ \mathop {\lim }\limits_{x \to 0} \frac{|x|}{|x|+x^2}= $$

The value of $\int_{-3}^3 \sin ^7 x \cos ^{16} x \mathrm{~d} x$ is

The coordinates of the foot of the perpendicular drawn from a point $\mathrm{P}(-1,1,2)$ to the plane $2 x-3 y+z-11=0$ are

The domain of the function $\mathrm{f}(x)={ }^{7-x} \mathrm{P}_{x-1}$ is

$$ \int \frac{x+\sin x}{1+\cos x} d x= $$

If $\bar{a}, \bar{b}, \bar{c}$ are three vectors such that $|\bar{a}|=3$, $|\bar{b}|=5,|\bar{c}|=7$ then $|\bar{a}-\bar{b}|^2+|\bar{b}-\bar{c}|^2+|\bar{c}-\bar{a}|^2$ does not exceed

Total number of 3-digit numbers, whose g.c.d with 36 is 2 , is

If $\frac{z-1}{2 z+1}$ is an imaginary number and if it represents a circle then its radius is

If $\int \tan ^4 x \mathrm{~d} x=\mathrm{a} \tan ^3 x+\mathrm{b} \tan x+\mathrm{c} x+\mathrm{k}$ (where k is the constant of integration) then the value of $\mathrm{a}-\mathrm{b}+\mathrm{c}=$

The lines $\frac{x-3}{1}=\frac{y-2}{1}=\frac{z-5}{-k}$ and $\frac{x-4}{\mathrm{k}}=\frac{y-3}{1}=\frac{\mathrm{z}-3}{2}$ are coplanar, hence $\mathrm{k}=$

$$ \int \frac{x \mathrm{~d} x}{(x-1)(x-2)}= $$

Let $A$ and $B$ are independent events with $\mathrm{P}(\mathrm{B})=\frac{2}{5}, \mathrm{P}(\mathrm{A} \cup \mathrm{B})=\frac{11}{20}$, then $\mathrm{P}\left(\mathrm{A}^{\prime} \mid \mathrm{B}\right)$ is root of the equation

The equation of tangent to the curve $y=\cos (x+y)$ where $-2 \pi \leq x \leq 2 \pi$ and which is parallel to the line $x+2 y=0$, is

The eccentricity of the ellipse $9 x^2+5 y^2-30 y=0$ is

If the tangent at $(1,7)$ to the curve $x^2=y-6$ touches the circle $x^2+y^2+16 x+12 y+\mathrm{C}=0$, then $\mathrm{C}=$

If the shortest distance between the lines $\bar{r}_1=\alpha \hat{i}+2 \hat{j}+2 \hat{k}+\lambda(\hat{i}-2 \hat{j}+2 \hat{k}), \lambda \in \mathbb{R}, \alpha>0 \quad$ and $\bar{r}_2=-4 \hat{i}-\hat{k}+\mu(3 \hat{i}-2 \hat{j}-2 \hat{k}), \mu \in R$, is 9 , then the value of $\alpha$ is

If two curves $x^2-4 y^2=2$ and $8 x^2=40-\mathrm{m} y^2$ are orthogonal to each other then $\mathrm{m}=$

The resultant of two vectors $\vec{A}$ and $\vec{B}$ is $\vec{C}$. If the magnitude of $\vec{B}$ is doubled, the new resultant vector becomes perpendicular to $\vec{A}$, then the magnitude of $\overrightarrow{\mathrm{C}}$ is

A convex lens of focal length $\frac{1}{3} \mathrm{~m}$ forms a real, inverted image twice the size of the object. The distance of the object from the lens is

The frequency of a tuning fork is 256 Hz . It will not resonate with the tuning fork of frequency

A particle carrying a charge equal to 1000 times the charge on an electron, is rotating one rotation per second in a circular path of radius ' $r$ ' $m$. If the magnetic field produced at the centre of the path is $x$ times the permeability of vacuum, the radius ' r ' in m is $\left[\mathrm{e}=1.6 \times 10^{-19} \mathrm{C}\right]\left[\mathrm{x}=2 \times 10^{-16}\right]$

A particle performing uniform circular motion of radius $\frac{\pi}{2} \mathrm{~m}$ makes $x$ revolutions in time $t$. Its tangential velocity is

The frequency of revolution of an electron in the $\mathrm{n}^{\text {th }}$ orbit of hydrogen atom is

The initial and final temperatures of water as recorded by an observer are $(38.6 \pm 0.2){ }^{\circ} \mathrm{C}$ and $(82.3 \pm 0.3){ }^{\circ} \mathrm{C}$. The rise in temperature with proper error limits is

' $n$ ' small water drops of same size (radius $r$ ) fall through air with constant velocity V. They coalesce to form a big drop of radius R . The terminal velocity of the big drop is

A vertical spring oscillates with period 6 second with mass $m$ is suspended from it. When the mass is at rest, the spring is stretched through a distance of (Take, acceleration due to gravity, $\mathrm{g}=\pi^2=10 \mathrm{~m} / \mathrm{s}^2$ )

The electric potential ' V ' is given as a function of distance ' $x$ ' (metre) by $V=\left(4 x^2+8 x-3\right) V$. The value of electric field at $x=0.5 \mathrm{~m}$, in $\mathrm{V} / \mathrm{m}$ is

Out of the following which law obeys the law of conservation of energy?

In a given logic circuit, the output Y when all the three inputs $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are first low and then high will be respectively

Two gases A and B are at absolute temperatures 350 K and 420 K respectively. The ratio of average kinetic energy of the molecules of gas $B$ to that of gas A is

For a particle performing; S.H.M. the displacement - time graph is shown.

For that particle the force - time graph is correctly shown in graph

A coil of resistance $450 \Omega$ and self-inductance 1.5 henry is connected to an a.c. source of frequency $\frac{150}{\pi} \mathrm{~Hz}$. The phase difference between voltage and current is

A small metal sphere of density $\rho$ is dropped from height $h$ into a jar containing liquid of density $\sigma(\sigma>\rho)$. The maximum depth up to which the sphere sinks is (Neglect damping forces)

A composite slab consists of two materials having coefficients of thermal conductivity K and $2 K$, thickness $x$ and $4 x$ respectively. The temperatures of two outer surfaces of a composite slab are $\mathrm{T}_2$ and $\mathrm{T}_1$ respectively $\left(\mathrm{T}_2>\mathrm{T}_1\right)$. The rate of heat transfer through the slab in a steady state is $\left[\frac{A\left(T_2-T_1\right) K}{x}\right] f$, where $f$ is equal to

In an organ pipe closed at one end; the sum of the frequencies of first three overtones is 3930 Hz . The frequency of the fundamental mode of organ pipe is

A uniformly charged conducting sphere of diameter 3.5 cm has a surface charge density of $20 \mu \mathrm{Cm}^{-2}$. The total electric flux leaving the surface of the sphere is nearly [permittivity of free space, $\varepsilon_0=8.85 \times 10^{-12} \mathrm{SI}$ unit]

A stone is projected with kinetic energy E, making an angle $\theta$ with the horizontal. When it reaches a highest point, its kinetic energy is

In Young's double slit experiment, the intensity on screen at a point where path difference is $\frac{\lambda}{4}$ is $\frac{K}{2}$. The intensity at a point when path difference is ' $\lambda$ ' will be

If $M$ is the magnetisation induced in the material, H is the magnetic field intensity, B is the net magnetic field inside the material then the correct relation between them is ( $\mu_0=$ permeability of free space)

Force is applied to a body of mass 3 kg at rest on a frictionless horizontal surface as shown in the force against time (F-t) graph. The speed of the body after 1 s is

An electron accelerated by a potential difference ' $V$ ' has de-Broglie wavelength ' $\lambda$ '. If the electron is accelerated by a potential difference ' 9 V ', its de-Broglie wavelength will be

A weightless thread can bear tension up to 3.7 kg wt. A stone of mass 500 gram is tied to it and revolved in circular path of radius 4 m in vertical plane. Maximum angular velocity of the stone will be (acceleration due to gravity, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$ )

Water is flowing steadily in a river. A and B are the two layers of water at heights 40 cm and 90 cm from the bottom. The velocity of the layer A is $12 \mathrm{~cm} / \mathrm{s}$. The velocity of the layer B is

A progressive wave of frequency 400 Hz is travelling with velocity $336 \mathrm{~m} / \mathrm{s}$. How far apart are the two points on a wave which are $60^{\circ}$ out of phase?

The magnetic flux through a coil is $4 \times 10^{-4} \mathrm{~Wb}$ at time $t=0$. It reduces to $30 \%$ of its original value in time $t$ second. If e.m.f. induced in the coil is 0.56 mV then the value of $t$ is

Bohr model is applied to a particle of mass m and charge $q$ is moving in a plane under the influence of a transverse magnetic field (B). The energy of the charged particle in the second level will be ( $\mathrm{h}=$ Planck's constant)

The co-efficient of absorption and the coefficient of reflection of a thin uniform plate are 0.77 and 0.17 respectively. If 250 kcal of heat is incident on the surface of the plate, the quantity of heat transmitted is

In Fraunhofer diffraction pattern, slit width is 0.2 mm and screen is at 2 m away from the lens. If the distance between the first minimum on either side of the central maximum is 1 cm , the wavelength of light used is

If $L$ is the inductance and $R$ is the resistance then the SI unit of $\frac{L}{R}$ is

In an $L-R$ circuit, the inductive reactance is equal to $\sqrt{3}$ times the resistance ' $R$ ' of the circuit. An e.1n.f. $\mathrm{E}=\mathrm{E}_0 \sin (\omega \mathrm{t})$ is applied to the circuit. The power consumed in the circuit is

A charged particle of mass ' $m$ ' and charge ' $q$ ' is at rest. It is acce:lerated in a uniform electric field of intensity ' $E$ ' : for time ' $t$ '. The kinetic energy of the particles after time $t$ is

To determine the internal resistance of a cell with potentiometer, when the cell is shunted by a resistance of $5 \Omega$ the balancing length is 250 cm . When the cell is shunted by $20 \Omega$, the balancing length of potentiometer wire is 400 cm . The internal resistance , of the cell is

A body slides down a smooth inclined plane of inclination $\theta$ and reaches the bottom with velocity V . If the same body is a ring which rolls down the same inclined plane then linear velocity at the bottom of plane is

Two parallel plate air c apacitors of same capacity ' C ' are connected in parallel to a battery of e.m.f. ' $E$ '. Then one of the capacitors is completely filled with dielectric mnaterial of constant ' K '. The change in the effective capacity of the parallel combination is

An ideal gas at pressure ' P ' and temperature ' T ' is enclosed in a vessel of volume ' $V$ '. Some gas leaks through a hole from the vessel and the pressure of the enclosed gas falls to ' P '. Assuming that the temperature ture of the gas remains constant during the leakage , the number of moles of the gas that have leaked is

The escape velocity of a satellite from the surface of earth does NOT depend on

In unbiased p-n junction diode

If r.m.s. velocity of hydrogen molecules is 4 times that of an oxygen molecule at $47^{\circ} \mathrm{C}$, the temperature of hydrogen molecules is (Molecular weight of Hydrogen and Oxygen are 2 and 32 respectively)

Two cells $E_1$ and $E_2$ having equal e.m.f ' $E$ ' and internal resistances $r_1$ and $r_2\left(r_1>r_2\right)$ respectively are connected in series. This combination is connected to an external resistance ' R '. It is observed that the potential difference across the cell $E_1$ becomes zero. The value of $R$ will be

If the length of the oscillating simple pendulum is made $\frac{1}{3}$ times the original keeping amplitude same then increase in its total energy at a place will be

Two long conductors separated by a distance ' d ' carry currents ' $\mathrm{I}_1$ ' and ' $\mathrm{I}_2$ ' in the same directions. They exert a force ' $F$ ' on each other. The distance between them is increased to ' 3 d '. If new repulsive force of magnitude ' $\frac{2}{3} \mathrm{~F}$ ' is found between these conductors, the required change in the magnitude and direction of one of the currents in the conductor is respectively [length of the conductors is constant]

In a transistor amplifier, AC current gain is 64 , the load resistance is $5400 \Omega$ and the input resistance of the transistor is $540 \Omega$. The voltage gain is

A monoatomic ideal gas is heated at constant pressure. The percentage of total heat used in increasing the internal energy and that used for doing external work is $A$ and $B$ respectively. Then the ratio, $\mathrm{A}: \mathrm{B}$ is

An a.c. source is applied to a series LR circuit with $\mathrm{X}_{\mathrm{L}}=3 \mathrm{R}$ and power factor is $\mathrm{X}_1$. Now a capacitor with $\mathrm{X}_{\mathrm{c}}=\mathrm{R}$ is added in series to LR circuit and the power factor is $\mathrm{X}_2$. The ratio $\mathrm{X}_1$ to $\mathrm{X}_2$ is

When two tuning forks are sounded together, 6 beats per second are heard. One of the fork is in unison with 0.70 m length of sonometer wire and another fork is in unison with 0.69 m length of the same sonometer wire. The frequencies of the two tuning forks are

The maximum velocity of the photoelectrons emitted by a metal surface is $9 \times 10^5 \mathrm{~m} / \mathrm{s}$. The value of ratio of charge (e) to mass (m) of the photoelectron is $1.8 \times 10^{11} \mathrm{C} / \mathrm{kg}$. The value of stopping potential in volt is

In Young's double slit experiment let 'd' be the distance between two slits and 'D' be the distance between the slits and the screen. Using a monochromatic source of wavelength ' $\lambda$ ', in an interference pattern, third minimum is observed exactly in front of one of the slits. If at the same point on the screen first minimum is to be obtained, the required change in the wavelength is [ $\mathrm{d} \& \mathrm{D}$ are not changed].