The subset-sum problem is defined as follows. Given a set of n positive integers, S = {a₁ ,a₂ ,a₃ ,…,a_n} and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2-dimensional Boolean array X, with n rows and W+1 columns. X[i, j], 1 <= i <= n, 0 <= j <= W, is TRUE if and only if there is a subset of {a₁ ,a₂ ,…,a_i} whose elements sum to j.

Which entry of the array X, if TRUE, implies that there is a subset whose elements sum to W?

The subset-sum problem is defined as follows. Given a set of n positive integers, S = {a₁ ,a₂ ,a₃ ,…,a_n} and positive integer W, is there a subset of S whose elements sum to W? A dynamic program for solving this problem uses a 2-dimensional Boolean array X, with n rows and W+1 columns. X[i, j], 1 <= i <= n, 0 <= j <= W, is TRUE if and only if there is a subset of {a₁ ,a₂ ,…,a_i} whose elements sum to j.
Which of the following is valid for 2 <= i <= n and ai <= j <= W?

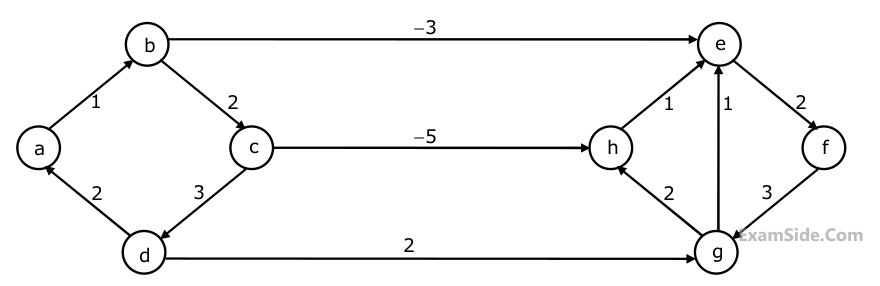Dijkstra's single source shortest path algorithm when run from vertex a in the above graph, computes the correct shortest path distance to

Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then