A complete binary min-heap is made by including each integer in $$[1,1023]$$ exactly once. The depth of a node in the heap is the length of the path from the root of the heap to that node. Thus, the root is at depth $$0.$$ The maximum depth at which integer $$9$$ can appear is ___________.

The Floyd-Warshall algorithm for all-pair shortest paths computation is based on

The given diagram shows the flowchart for a recursive function $$A(n).$$ Assume that all statements, except for the recursive calls, have $$O(1)$$ time complexity. If the worst case time complexity of this function is $$O\left( {{n^\alpha }} \right),$$ then the least possible value (accurate up to two decimal positions) of $$\alpha $$ is ____________ .

Let $${A_1},{A_2},{A_3},$$ and $${A_4}$$ be four matrices of dimensions $$10 \times 5,\,\,5 \times 20,\,\,20 \times 10,$$ and $$10 \times 5,\,$$ respectively. The minimum number of scalar multiplications required to find the product $${A_1}{A_2}{A_3}{A_4}$$ using the basic matrix multiplication method is ______________.

Assume that the algorithms considered here sort the input sequences in ascending order. If the input is already in ascending order, which of the following are TRUE?

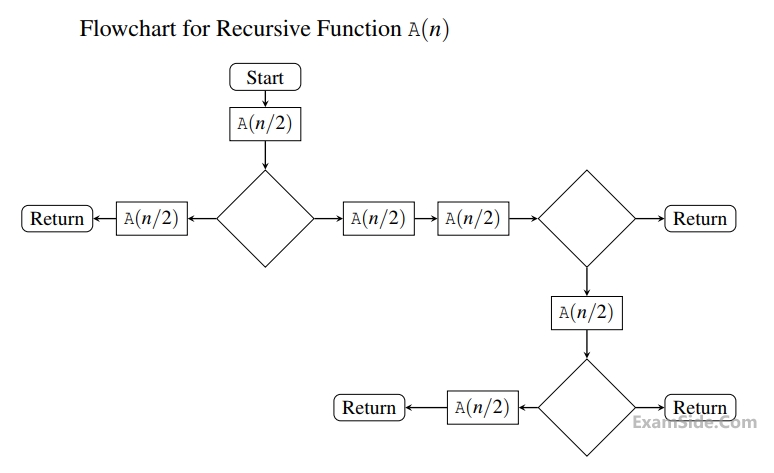
$$\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,\,\,$$ Quicksort runs in $$\Theta \left( {{n^2}} \right)$$ time
$$\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,\,\,$$ Bubblesort runs in $$\Theta \left( {{n^2}} \right)$$ time
$$\,\,\,{\rm I}{\rm I}{\rm I}.\,\,\,\,\,\,\,$$ Mergesort runs in $$\Theta \left( n \right)$$ time
$$\,\,\,{\rm I}V.\,\,\,\,\,\,\,$$ Insertion sort runs in $$\Theta \left( n \right)$$ time

Match the following:

GROUP - 1	GROUP - 2
(P) Lexical analysis	(i) Leftmost derivation
(Q) Top down parsing	(ii) Type checking
(R) Semantic analysis	(iii) Regular expressions
(S) Runtime environments	(iv) Activation records

Which one of the following grammars is free from $$left$$ $$recursion$$?

A student wrote two context-free grammars G1 and G2 for generating a single $$C$$-like array declaration. The dimension of the array is at least one. For example, $$${\mathop{\rm int}} \,\,\,\,\,\,\,a[10]\,\,[3];$$$

The grammars use D as the start symbol, and use six terminal symbols int ; id [ ] num.

Grammar G1	Grammar G2
D → intL;	D → intL;
L → id[E	L → idE
E → num	E → E[num]
E → num][E	E → [num]

Which of the grammars correctly generate the declaration mentioned above?

In an Ethernet local area network, which one of the following statements is TRUE?

For the IEEE 802.11 MAC protocol for wireless communication, which of the following statements is/are TRUE?

I. At least three non-overlapping channels are available for transmissions.
II. The RTS-CTS mechanism is used for collision detection.
III. Unicast frames are ACKed.

A network has a data transmission bandwidth of 20 × 10⁶ bits per second. It uses CSMA/CD in the MAC layer. The maximum signal propagation time from one node to another node is 40 microseconds. The minimum size of a frame in the network is __________ bytes.

Consider a 128 × 10³ bits/second satellite communication link with one way propagation delay of 150 milliseconds. Selective retransmission (repeat) protocol is used on this link to send data with a frame size of 1 kilobyte. Neglect the transmission time of acknowledgement. The minimum number of bits required for the sequence number field to achieve 100% utilization is _________.

Identify the correct sequence in which the following packets are transmitted on the network by a host when a browser requests a webpage from a remote server, assuming that the host has just been restarted.

Anarkali digitally signs a message and sends it to Salim. Verification of the signature by Salim requires

Suppose the functions $$F$$ and $$G$$ can be computed in $$5$$ and $$3$$ nanoseconds by functional units $${U_F}$$ and $${U_G},$$ respectively. Given two instances of $${U_F}$$ and two instances of $${U_G},$$ it is required to implement the computation $$F\left( {G\left( {{X_i}} \right)} \right)$$ for $$1 \le i \le 10.$$ Ignoring all other delays, the minimum time required to complete this computation is _____________ nanoseconds.

Consider a processor with $$64$$ registers and an instruction set of size twelve. Each instruction has five distinct fields, namely, opcode, two source register identifiers, one destination register identifier, and a twelve-bit immediate value. Each instruction must be stored in memory in a byte-aligned fashion. If a program has $$100$$ instructions, the amount of memory (in bytes) consumed by the program text is _____________.

The width of the physical address on a machine is $$40$$ bits. The width of the tag field in a $$512$$ $$KB$$ $$8$$-way set associative cache is _____________ bits.

Consider a $$3$$ $$GHz$$ (gigahertz) processor with a three-stage pipeline and stage latencies $${\tau _1},{\tau _2},$$ and $${\tau _3}$$ such that $${\tau _1} = 3{\tau _2}/4 = 2{\tau _3}.$$ If the longest pipeline stage is split into two pipeline stages of equal latency, the new frequency is ____________ $$GHz,$$ ignoring delays in the pipeline registers.

A file system uses an in-memory cache to cache disk blocks. The miss rate of the cache is shown in the figure. The latency to read a block from the cache is $$1$$ $$ms$$ and to read a block from the disk is $$10$$ $$ms.$$ Assume that the cost of checking whether a block exists in the cache is negligible. Available cache sizes are in multiples of $$10$$ $$MB.$$

The smallest cache size required to ensure an average read latency of less than $$6$$ $$ms$$ is _________ $$MB.$$

A processor has $$40$$ distinct instructions and $$24$$ general purpose registers. A $$32$$-bit instruction word has an opcode, two register operands and an immediate operand. The number of bits available for the immediate operand field is __________ .

Consider the following $$New-order$$ strategy for traversing a binary tree:

$$\,\,\,\,\,\,\, \bullet \,\,\,\,\,$$ Visit the root;
$$\,\,\,\,\,\,\, \bullet \,\,\,\,\,$$ Visit the right subtree using $$New-order;$$
$$\,\,\,\,\,\,\, \bullet \,\,\,\,\,$$ Visit the left subtree using $$New-order;$$

The New-order traversal of the expression tree corresponding to the reverse polish expression 3 4 * 5 - 2 ^ 6 7 * 1 + - is given by:

In an adjacency list representation of an undirected simple graph $$G = (V,E),$$ each edge $$(u, v)$$ has two adjacency list entries: $$[v]$$ in the adjacency list of $$u,$$ and $$[u]$$ in the adjacency list of $$v.$$ These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If $$|E| = m$$ and $$|V| = n,$$ and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?

The number of ways in which the numbers $$1, 2, 3, 4, 5, 6, 7$$ can be inserted in an empty binary search tree, such that the resulting tree has height $$6,$$ is _____________.

$$Note:\,\,\,The\,\,height\,\,of\,\,a\,tree\,\,with\,\,a\,\,\sin gle\,\,node\,\,is\,\,0$$

Breadth First Search $$(BFS)$$ is started on a binary tree beginning from the root vertex. There is a vertex $$t$$ at a distance four from the root. If t is the $$n$$-th vertex in this $$BFS$$ traversal, then the maximum possible value of $$n$$ is ___________.

$$N$$ items are stored in a sorted doubly linked list. For a $$delete$$ operation, a pointer is provided to the record to be deleted. For a $$decrease$$-$$key$$ operation, a pointer is provided to the record on which the operation is to be performed.

An algorithm performs the following operations on the list in this order:
$$\Theta \left( N \right),\,\,delete,\,\,O\left( {\log N} \right)\,insert,\,$$ $$\,O\left( {\log N} \right)\,fund, and $$ $$\Theta \left( N \right)\,$$ $$decrease$$-$$key.$$ What is the time complexity of all these operations put together?

Suppose a database schedule $$S$$ involves transactions $${T_1},\,...,\,{T_n}.$$ Construct the precedence graph of $$S$$ with vertices representing the transactions and edges representing the conflicts. If $$S$$ is serializable, which one of the following orderings of the vertices of the precedence graph is guaranteed to yield a serial schedule?

Consider the following database schedule with two transactions, T₁ and T₂

 S = r2(X); r1(X); r2(Y); w1(X); r1(Y); w2(X); a1; a2

where r_i(Z) denotes a read operation by transaction T_i on a variable Z, w_i(Z) denotes a write operation by T_i on a variable Z and a_i denotes an abort by transaction T_i .

Which one of the following statements about the above schedule is TRUE?

Consider the following database table named $$water$$_$$schemes :$$

	water_schemes
scheme_no	district_name	capacity
1	Ajmer	20
1	Bikaner	10
2	Bikaner	10
3	Bikaner	20
1	Churu	10
2	Churu	20
1	Dungargarh	10

The number of tuples returned by the following $$SQL$$ query is _______________.

with total(name, capacity) as
    select district_name, sum(capacity)
    from water_schemes
    group by district_name
with total_avg(capacity) as
    select avg(capacity)
    from total
select name
    from total, total_avg
    where total.capacity ≥ total_avg.capacity

B⁺ Trees are considered BALANCED because

Consider an eight-bit ripple-carry adder for computing the sum of $$A$$ and $$B,$$ where $$A$$ and $$B$$ are integers represented in $$2’s$$ complement form. If the decimal value of $$A$$ is one, the decimal value of $$B$$ that leads to the longest latency for the sum to stabilize is __________ .

Let, $${x_1} \oplus {x_2} \oplus {x_3} \oplus {x_4} = 0$$ where $${x_1},\,{x_2},\,{x_3},\,{x_4}$$ are Boolean Variables, and $$ \oplus $$ is the $$XOR$$ operator.

Which one of the following must always be TRUE?

Let $$X$$ be the number of distinct $$16$$-bit integers in $$2’s$$ complement representation. Let $$Y$$ be the number of distinct $$16$$-bit integers in sign magnitude representation.
Then $$X −Y$$ is ____________.

A binary relation $$R$$ on $$N \times N$$ is defined as follows: $$(a,b)R(c,d)$$ if $$a \le c$$ or $$b \le d.$$ Consider the following propositions:

$$P:$$ $$R$$ is reflexive
$$Q:$$ $$R$$ is transitive

Which one of the following statements is TRUE?

Consider a set $$U$$ of $$23$$ different compounds in a Chemistry lab. There is a subset $$S$$ of $$U$$ of $$9$$ compounds, each of which reacts with exactly $$3$$ compounds of $$U.$$ Consider the following statements:

$$\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,$$ Each compound in $$U \ S$$ reacts with an odd number of compounds.
$$\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,$$ At least one compound in $$U \ S$$ reacts with an odd number of compounds.
$$\,\,\,{\rm I}{\rm I}{\rm I}.\,\,\,\,\,$$ Each compound in $$U \ S$$ reacts with an even number of compounds.

Which one of the above statements is ALWAYS TRUE?

Which one of the following well-formed formulae in predicate calculus is NOT valid?

The value of the expression $${13^{99}}$$ ($$mod$$ $$17$$), in the range $$0$$ to $$16,$$ is ______________ .

Consider the system, each consisting of m linear equations in $$n$$ variables.
$$I.$$ $$\,\,\,$$ If $$m < n,$$ then all such system have a solution
$$II.$$ $$\,\,\,$$ If $$m > n,$$ then none of these systems has a solution
$$III.$$ $$\,\,\,$$ If $$m = n,$$ then there exists a system which has a solution

Which one of the following is CORRECT?

Let $${A_1},\,{A_2},\,{A_3}$$ and $${A_4}$$ be four matrices of dimensions $$10 \times 5,\,5 \times 20,\,20 \times 10,$$ and $$10 \times 5,$$ respectively. The minimum number of scalar multiplications required to find the product $${A_1}{A_2}{A_3}{A_4}$$ using the basic matrix multiplication method is _________.

Suppose that a shop has an equal number of LED bulbs of two different types. The probability of an LED bulb lasting more than $$100$$ hours given that it is of Type $$1$$ is $$0.7,$$ and given that it is of Type $$2$$ is $$0.4.$$ The probability that an LED bulb chosen uniformly at random lasts more than $$100$$ hours is _________.

Suppose that the eigen values of matrix $$A$$ are $$1, 2, 4.$$ The determinant of $${\left( {{A^{ - 1}}} \right)^T}$$ is _______.

Consider the following expressions:
$$\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$(i)$$ $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ false
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$(ii)$$ $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$Q$$
$$\,\,\,\,\,\,\,\,\,\,\,$$ $$(iii)$$ $$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ true
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$(iv)$$ $$\,\,\,\,\,\,\,\,\,\,\,$$ $$P∨Q$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$(v)$$ $$\,\,\,\,\,\,\,\,\,\,\,\,$$ $$\neg QVP$$

The number of expressions given above that are logically implied by $$P \wedge \left( {P \Rightarrow Q} \right)$$) is _____________.

Let $$f(x)$$ be a polynomial and $$g\left( x \right) = f'\left( x \right)$$ be its derivative. If the degree of $$\left( {f\left( x \right) + f\left( { - x} \right)} \right)$$ is $$10,$$ then the degree of $$\left( {g\left( x \right) - g\left( { - x} \right)} \right)$$ is ___________.

The minimum number of colours that is sufficient to vertex-colour any planar graph is _____________ .

In which one of the following page replacement algorithms it is possible for the page fault rate to increase even when the number of allocated frames increases?

Consider the following processes, with the arrival time and the length of the CPU burst given in milliseconds. The scheduling algorithm used is preemptive shortest remaining-time first.

Process	Arrival Time	Burst Time
P1 P2 P3 P4	0 3 7 8	10 6 1 3

The average turn around time of these processes is milliseconds.

Consider a non-negative counting semaphore $$S.$$ The operation $$P(S)$$ decrements $$S,$$ and $$V(S)$$ increments $$S.$$ During an execution, $$20$$ $$P(S)$$ operations and $$12$$ $$V(S)$$ operations are issued in some order. The largest initial value of $$S$$ for which at least one $$P(S)$$ operation will remain blocked is _____________ .

The number of states in the minimum sized $$DFA$$ that accepts the language defined by the regular expression $$${\left( {0 + 1} \right)^ * }\left( {0 + 1} \right){\left( {0 + 1} \right)^ * }$$$
is ___________________.

Language $${L_1}$$ is defined by the grammar: $$S{}_1 \to a{S_1}b|\varepsilon $$
Language $${L_2}$$ is defined by the grammar: $$S{}_2 \to ab{S_2}|\varepsilon $$

Consider the following statements:
$$P:$$ $${L_1}$$ is regular
$$Q:$$ $${L_2}$$ is regular

Which one of the following is TRUE?

Consider the following types of languages: $${L_1}:$$ Regular, $${L_2}:$$ Context-free, $${L_3}:$$ Recursive, $${L_4}:$$ Recursively enumerable. Which of the following is/are TRUE?

$$\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,\,\,$$ $$\overline {{L_3}} \cup {L_4}$$ is recursively enumerable
$$\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,\,\,$$ $$\overline {{L_2}} \cup {L_3}$$ is recursive
$$\,\,\,{\rm I}{\rm I}{\rm I}.\,\,\,\,\,\,\,$$ $$L_1^ * \cap {L_2}$$ is context-free
$$\,\,\,{\rm I}V.\,\,\,\,\,\,\,$$ $${L_1} \cup \overline {{L_2}} $$ is context-free

Consider the following two statements :

$$\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,$$ If all states of an $$NFA$$ are accepting states then the language accepted by the
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$NFA$$ is $$\sum {^ * } .$$
$$\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,$$ There exists a regular language $$A$$ such that for all languages $$B,A \cap B$$ is
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ regular.

Which one of the following is CORRECT?

Consider the following languages : $$$\eqalign{ & {L_1} = \left\{ {{a^n}{b^m}{c^{n + m}}:m,n \ge 1} \right\} \cr & {L_2} = \left\{ {{a^n}{b^n}{c^{2n}}:n \ge 1} \right\} \cr} $$$

Which one of the following is TRUE?

Consider the following languages.

$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $${L_1} = \left\{ {\left\langle M \right\rangle |M} \right.$$ takes at least $$2016$$ steps on some input $$\left. \, \right\},$$
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $${L_2} = \left\{ {\left\langle M \right\rangle |M} \right.$$ takes at least $$2016$$ steps on all inputs $$\left. \, \right\}$$ and
$$\,\,\,\,\,\,\,\,\,\,\,\,$$ $${L_3} = \left\{ {\left\langle M \right\rangle |M} \right.$$ accepts $$\left. \varepsilon \right\},$$

where for each Turing machine $${M,\left\langle M \right\rangle }$$ denotes a specific encoding of $$M.$$ Which one of the following is TRUE?

All hill-stations have a lake. Ooty has two lakes.

Which of the statement(s) below is/are logically valid and can be inferred from the above sentences?

$$\,\,\,\,\,\,\,\,\,$$$$(i)$$ $$\,\,\,\,\,\,\,\,\,\,$$ Ooty is not a hill-station.
$$\,\,\,\,\,\,\,$$ $$(ii)$$ $$\,\,\,\,\,\,\,\,\,$$ No hill-station can have more than one lake.

The man who is now Municipal Commissioner worked as ____________________.

Nobody knows how the Indian cricket team is going to cope with the difficult and seamer-friendly wickets in Australia.

Choose the option which is closest in meaning to the underlined phrase in the above sentence.

Find the odd one in the following group of words

mock, deride, praise, jeer

Pick the odd one from the following options.

In a quadratic function, the value of the product of the roots $$\left( {\alpha ,\beta } \right)$$ is $$4.$$ Find the value of $$${{{\alpha ^n} + {\beta ^n}} \over {{\alpha ^{ - n}} + {\beta ^{ - n}}}}$$$

Among $$150$$ faculty members in an institute, $$55$$ are connected with each other through Facebook^® and $$85$$ are connected through WhatsApp^®. $$30$$ faculty members do not have Facebook^® or whatsApp^® accounts. The number of faculty members connected only through Facebook^® accounts is ______________.

Computers were invented for performing only high-end useful computations. However, it is no understatement that they have taken over our world today. The internet, for example, is ubiquitous. Many believe that the internet itself is an unintended consequence of the original invention. With the advent of mobile computing on our phones, a whole new dimension is now enabled. One is left wondering if all these developments are good or, more importantly, required.

Which of the statement(s) below is/are logically valid and can be inferred from the above paragraph?

$$\,\,\,\,\,\,\,\,\,$$$$(i)$$ $$\,\,\,\,\,\,\,\,\,$$ The author believes that computers are not good for us.
$$\,\,\,\,\,\,\,$$ $$(ii)$$ $$\,\,\,\,\,\,\,\,\,$$ Mobile computers and the internet are both intended inventions

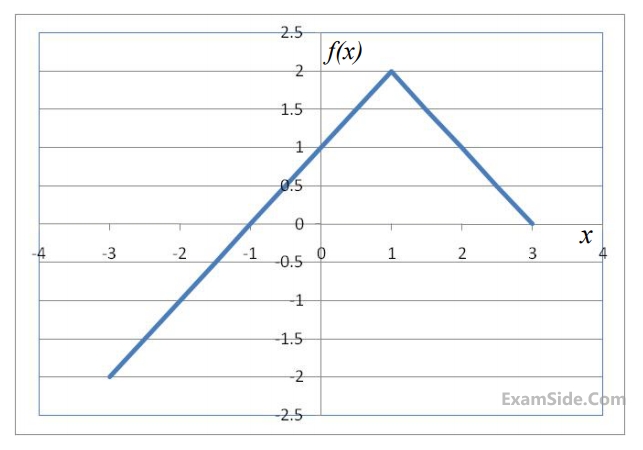
Choose the correct expression for $$f(x)$$ given in the graph.

In a $$2 \times 4$$ rectangle grid shown below, each cell is a rectangle. How many rectangles can be observed in the grid?