Which of the given options provides the increasing order of asymptotic Complexity of functions f₁, f₂, f₃ and f₄?
f₁ = 2ⁿ f₂ = n^3/2
f₃(n) = $$n\,\log _2^n$$
f₄ (n) = n ^log₂n

A max-heap is a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap?

An undirected graph G(V, E) contains n ( n > 2 ) nodes named v₁ , v₂ ,….v_n. Two nodes v_i , v_j are connected if and only if 0 < |i – j| <= 2. Each edge (v_i, v_j ) is assigned a weight i + j. A sample graph with n = 4 is shown below. What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?

An undirected graph G(V, E) contains n ( n > 2 ) nodes named v₁ , v₂ ,….v_n. Two nodes v_i , v_j are connected if and only if 0 < |i – j| <= 2. Each edge (v_i, v_j ) is assigned a weight i + j. A sample graph with n = 4 is shown below. The length of the path from v5 to v6 in the MST of previous question with n = 10 is

An algorithm to find the length of the longest monotonically increasing sequence of numbers in an array A[0:n−1] is given below.

Let L_i, denote the length of the longest monotonically increasing sequence starting at index i in the array. Initialize L_n−1=1.

For all i such that $$0 \leq i \leq n-2$$

$$L_i = \begin{cases} 1+ L_{i+1} & \quad\text{if A[i] < A[i+1]} \\ 1 & \quad\text{Otherwise}\end{cases}$$

Finally, the length of the longest monotonically increasing sequence is max(L₀, L₁,…,L_n−1)
Which of the following statements is TRUE?

Four matrices M₁, M₂, M₃ and M₄ of dimensions p $$\times$$ q, q $$\times$$ r, r $$\times$$ s and s $$\times$$ t respectively can be multiplied is several ways with different number of total scalar multiplications. For example, when multiplied as ((M₁ $$\times$$ M₂) $$\times$$ (M₃ $$\times$$ M₄)), the total number of multiplications is pqr + rst + prt. When multiplied as (((M₁ $$\times$$ M₂) $$\times$$ M₃) $$\times$$ M₄), the total number of scalar multiplications is pqr + prs + pst.

If p = 10, q = 100, r = 20, s = 5 and t = 80, then the number of scalar multiplications needed is:

In a compiler, keywords of a language are recognized during

Consider a network with five nodes, N1 to N5, as shown below.

The network uses a Distance Vector Routing protocol. Once the routes have stabilized, the distance vectors at different nodes are as following

N1 : ( 0, 1, 7, 8, 4 )
N2 : ( 1, 0, 6, 7, 3 )
N3 : ( 7, 6, 0, 2, 6 )
N4 : ( 8, 7, 2, 0, 4 )
N5 : ( 4, 3, 6, 4, 0 )

Each distance vector is the distance of the best known path at that instance to nodes, N1 to N5, where the distance to itself is 0. Also, all links are symmetric and the cost is identical in both directions. In each round, all nodes exchange their distance vectors with their respective neighbors. Then all nodes update their distance vectors. In between two rounds, any change in cost of a link will cause the two incident nodes to change only that entry in their distance vectors

After the update in the previous question, the link N1-N2 goes down. N2 will reflect this change immediately in its distance vector as cost, $$\infty $$. After the NEXT ROUND of update, what will be the cost to N1 in the distance vector of N3?

Consider a network with five nodes, N1 to N5, as shown below.

The network uses a Distance Vector Routing protocol. Once the routes have stabilized, the distance vectors at different nodes are as following

N1 : ( 0, 1, 7, 8, 4 )
N2 : ( 1, 0, 6, 7, 3 )
N3 : ( 7, 6, 0, 2, 6 )
N4 : ( 8, 7, 2, 0, 4 )
N5 : ( 4, 3, 6, 4, 0 )

Each distance vector is the distance of the best known path at that instance to nodes, N1 to N5, where the distance to itself is 0. Also, all links are symmetric and the cost is identical in both directions. In each round, all nodes exchange their distance vectors with their respective neighbors. Then all nodes update their distance vectors. In between two rounds, any change in cost of a link will cause the two incident nodes to change only that entry in their distance vectors

The cost of link N2 - N3 reduces to 2 in (both directions). After the next round of updates, what will be the new distance vector at node, N3?

Consider different activities related to email:

m1: Send an email from a mail client to a mail server
m2: Download an email from mailbox server to a mail client
m3: Checking email in a web browser

Which is the application level protocol used in each activity?

A layer-4 firewall (a device that can look at all protocol headers up to the transport layer) CANNOT

An $$8KB$$ direct-mapped write-back cache is organized as multiple blocks, each of size $$32$$-bytes. The processor generates $$32$$-bit addresses. The cache controller maintains the tag information for each cache block comprising of the following.
$$\,\,\,\,$$$$1$$ Valid bit
$$\,\,\,\,$$$$1$$ Modified bit

As many bits as the minimum needed to identify the memory block mapped in the cache.

What is the total size of memory needed at the cache controller to store meta-data (tags) for the cache?

Consider an instruction pipeline with four stages $$\left( {S1,\,S2,\,S3,} \right.$$ and $$\left. {S4} \right)$$ each with combinational circuit only. The pipeline registers are required between each stage and at the end of the last stage. Delays for the stages and for the pipeline registers are as given in the figure.

What is the approximate speed up of the pipeline in steady state under ideal conditions when compared to the corresponding non-pipeline implementation?

On a non-pipelined sequential processor, a program segment, which is a part of the interrupt service routine, is given to transfer $$500$$ bytes from an $${\rm I}/O$$ device to memory. Initialize the address register Initialize the count to $$500$$

$$LOOP:$$ Load a byte from device Store in memory at address given by address register
Increment the address register
Decrement the count
If count! $$=0$$ go to $$LOOP$$

Assume that each statement in this program is equivalent to a machine instruction which takes one clock cycle to execute if it is a non load/store instruction. The load-store instructions take two clock cycles to execute.

The designer of the system also has an alternate approach of using the $$DMA$$ controller to implement the same transfer. The $$DMA$$ controller requires $$20$$ clock cycles for initialization and other overheads. Each $$DMA$$ transfer cycle takes two clock cycles to transfer one byte of data from the device to the memory.

What is the approximate speed up when the $$DMA$$ controller based design is used in place of the interrupt driven program based input- output?

A computer handles several interrupt sources of which of the following are relevant for this question.

$$ * \,\,\,\,\,\,\,\,\,\,\,$$ Interrupt from $$CPU$$ temperature sensor (raises interrupt if $$CPU$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ temperature is too high)
$$ * \,\,\,\,\,\,\,\,\,\,\,$$ Interrupt from Mouse (raises interrupt if the mouse is moved or a button is
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$pressed)
$$ * \,\,\,\,\,\,\,\,\,\,\,$$ Interrupt from Keyboard (raises interrupt when a key is pressed or released)
$$ * \,\,\,\,\,\,\,\,\,\,\,$$ Interrupt from Hard Disk (raises interrupt when a disk read is completed)

Which one of these will be handled at the $$HIGHEST$$ priority?

On a non-pipe-lined sequential processor, a program segment, which is a part of the interrrupt service routine, is given to transfer $$500$$ bytes from an $${\rm I}/O$$ device to memory. Initialize the address register Initialize the count to $$500$$
$$LOOP:$$ Load a byte from device Store in memory at address given by address register $$$\eqalign{ & Increment\,\,\,the\,\,\,address\,\,register \cr & Decrement\,\,\,the\,\,count \cr & If\,\,\,count!\,\,\, = 0\,\,\,go\,\,\,to\,\,\,LOOP \cr} $$$

Assume that each statement in this program is equivalent to a machine instruction which takes one clock cycle to execute if it is non- load/store instruction. The load-store instructions take two clock cycles to execute.

The designer of the system also has an alternate approach of using the $$DMA$$ controller to implement the same transfer. The $$DMA$$ controller requires $$20$$ clock cycles for initialization and other overheads. Each $$DMA$$ transfer cycle takes two clock cycles to transfer one byte of data from the device to the memory.

What is the approximate speed up when the $$DMA$$ controller based design is used in place of the interrupt driven program based input-output?

We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with the given set so that it becomes a binary search tree?

A max-heap is a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap?

Database table by name Loan_Records is given below.

Borrower	Bank_Manager	Loan_Amount
Ramesh	Sunderajan	10000.00
Suresh	Ramgopal	5000.00
Mahesh	Sunderajan	7000.00

What is the output of the following SQL query?

SELECT count(*) 
FROM ( 
(SELECT Borrower. Bank_Manager FROM Loan_Records) AS S 
NATURAL JOIN 
(SELECT Bank_Manager, Loan_Amount FROM Loan_Records) AS T );

Consider a database table T containing two columns X and Y each of type integer. After the creation of the table, one record (X = 1, Y = 1) is inserted in the table.

Let MX and MY denote the respective maximum values of X and Y among all records in the table at any point in time. Using MX and MY, new records are inserted in the table 128 times with X and Y values being MX + 1, 2*MY + 1 respectively. It may be noted that each time after the insertion, values of MX and MY change.

What will be the output of the following SQL query after the steps mentioned above are carried out?

SELECT Y FROM T WHERE X=7; 

Consider a relational table r with sufficient number of records, having attributes A₁, A₂,....., A_n and let 1 $$ \le $$ p $$ \le $$ n. Two queries Q1 and Q2 are given below.

$$Q1: \pi_{A_1, \dots ,A_p} \left(\sigma_{A_p=c}\left(r\right)\right)$$ where is a constant

$$Q2: \pi_{A_1, \dots ,A_p} \left(\sigma_{c_1 \leq A_p \leq c_2}\left(r\right)\right)$$ where c₁ and c₂ are constants

The database can be configured to do ordered indexing on A_p or hashing on A_p. Which of the following statements is TRUE?

Consider a relation table with a single record for each registered student with a single record for each registered student with the following attributes.
$$1.$$ $$Registration$$ $$Num:$$ Unique registration number of each registered student.
$$2.$$ $$UID :$$ Unique identity number, unique at the national level for each cityzen.
$$3.$$ $$BankAccount_Num:$$ Unique account number at the bank. A student can have multiple accounts or joint accounts. This attribute stores the primary account number.
$$4.$$ $$Name:$$ Name of the student
$$5.$$ $$Hostel$$ $$Room:$$ Room number of the hostel.

Which of the following options is INCORRECT?

Which one of the following circuits is NOT equivalent to a $$2$$-input $$XNOR$$ (exclusive NOR) gate

The simplified $$SOP$$ (Sum of product) form of the Boolean expression
$$\left( {P + \overline Q + \overline R } \right).\left( {P + \overline Q + R} \right).\left( {P + Q + \overline R } \right)$$ is

Consider the following circuit involving three Dtypes flip-flops used in a certain type of Counter configuration.

If all the flip-flops were reset to $$0$$ at power on, what is the total number of distinct outputs (states) represented by $$PQR$$ generated by the counter?

Consider the following circuit involving three Dtypes flip-flops used in a certain type of Counter configuration.

If at some instance prior to the occurrence of the clock edge, $$P, Q$$ and $$R$$ have a value $$0,1$$ and $$0$$ respectively, what shall be the value of $$PQR$$ after the clock edge?

If the difference between the expectation of the square of a random variable $$\left( {E\left[ {{X^2}} \right]} \right)$$ and the square of the expectation of the random variable $${\left( {E\left[ X \right]} \right)^2}$$ is denoted by R then

A deck of 5 cards (each carrying a distinct number from 1 to 5) is shuffled thoroughly. Two cards are then removed one at a time from the deck. What is probability that the two cards are selected with the number on the first card is one higher than the number on the second card.

Which one of the following options is correct given three positive integers $$x, y$$ and $$z$$, and a predicate
$$P\left( x \right) = \neg \left( {x = 1} \right) \wedge \forall y\left( {\exists z\left( {x = y * z} \right) \Rightarrow \left( {y = x} \right) \vee \left( {y = 1} \right)} \right)$$

Given $$i = \sqrt { - 1} ,$$ what will be the evaluation of the definite integral $$\int\limits_0^{\pi /2} {{{\cos x +i \sin x} \over {\cos x - i\,\sin x}}dx?} $$

$$K4$$ and $$Q3$$ are graphs with the following structures.

Which one of the following statements is TRUE in relation to these graphs?

Four matrices $${M_1},\,\,\,{M_2},\,\,\,{M_3}$$ and $${M_4}$$ of dimensions $$p\,\,x\,\,q,\,\,\,\,\,q\,\,x\,\,e,\,\,\,\,\,r\,\,x\,\,s$$ and $$\,\,\,\,s\,\,x\,\,t$$ respectively can be multiplied in sevaral ways with different number of total scalar multiplications. For example when multiplied as $$\left( {\left( {{M_1}\,\,X\,\,{M_2}} \right)\,\,X\,\,\left( {{M_3}\,\,X\,\,{M_4}} \right)} \right)$$, the total number of scalar multiplications is $$\,\,\,\,$$$$pqr + rst + prt$$. When multiplied as $$\left( {\left( {\left( {{M_1}\,\,X\,\,{M_2}} \right)\,\,X\,\,{M_3}} \right)X\,\,{M_4}} \right)$$, the total number of scalar multiplications is $$pqr + prs + pst$$. If $$p = 10,\,\,q = 100,\,\,r = 20,\,\,s = 5,\,\,$$ and $$t = 80$$, then the minimum number of scalar multiplications needed is

Consider the matrix as given below. $$$\left[ {\matrix{ 1 & 2 & 3 \cr 0 & 4 & 7 \cr 0 & 0 & 3 \cr } } \right]$$$

Which of the following options provides the Correct values of the Eigen values of the matrix?

$$\left[ A \right]$$ is a square matrix which is neither symmetric nor skew-symmetric and $${\left[ A \right]^T}$$ is its transpose. The sum and differences of these matrices and defined as $$\left[ S \right] = \left[ A \right] + {\left[ A \right]^T}$$ and $$\left[ D \right] = \left[ A \right] - {\left[ A \right]^T}$$ respectively. Which of the following statements is true?

Consider a finite sequence of random values $$X = \left\{ {{x_1},{x_2},{x_3}, - - - - - {x_n}} \right\}..$$ Let $${\mu _x}$$ be the mean and $${\sigma _x}$$ be the standard deviation of $$X.$$ Let another finite sequence $$Y$$ of equal length be derived from this $${y_i} = a.{x_i} + b,$$ where $$a$$ and $$b$$ are positive constants. Let $${\mu _y}$$ be the mean and $${\sigma _y}$$ be the standard deviation of this sequence. Which one of the following statements is incorrect?

If two fair coins are flipped and at least one of the outcomes is known to be a head, what is the probability that both outcomes are heads?

An application loads $$100$$ libraries at startup. Loading each library requires exactly one disk access. The seek time of the disk to random location is given as $$10$$ $$ms$$. Rotational speed of disk is $$6000$$ $$rpm.$$ If all $$100$$ libraries are loaded from random locations on the disk, how long does it take to load all libraries? (The time to transfer data from the disk block once the head has been positioned at the start of the block may be neglected).

Let the time taken to switch between user and kernel modes of execution be $${t_1}$$ while the time taken to switch between two processes be $${t_2}$$.

Which of the following is TRUE?

A Computer handles several interrupt sources of which the following are relevant for this question:

$$ * \,\,\,$$ Interrupt from $$CPU$$ temperature sensor (raises interrupt if $$CPU$$ temperature is too high)

$$ * \,\,\,$$ Interrupt from Mouse (raises interrupt if the mouse is moved or a button is pressed)

$$ * \,\,\,$$ Interrupt from keyboard (raises interrupt when a key is pressed or release)

$$ * \,\,\,$$ Interrupt from Hard Disk (raises interrupt when a disk read is completed)>/p>

Which one these will be handled at the HIGHEST priority?

A thread is usually defined as a ''light weight process'' because an operating system $$(OS)$$ maintains smaller data structures for a thread than for a process. In relation to this, which of the following is TRUE?

Consider the following table of arrival time and burst time for three processes $$P0,P1$$ and $$P2$$.

Process	Arrival Time	Burst Time
P0	0 ms	9 ms
P1	1 ms	4 ms
P2	2 ms	9 ms

The pre-emptive shortest job first scheduling algorithm is used. Scheduling is carried out only a arrival or completion of processes. What is the average waiting time for the three processes?

What does the following fragment of C-program print?

char c[ ] = "GATE2011";
char *p = c;
printf("%s", p + p[3] - p[1]);

Consider the following recursive C function that takes two arguments:

unsigned int foo (unsigned int n, unsigned int r) {
  if (n > 0) return((n % r) + foo(n/r, r));
  else return 0;
}

What is the return value of the function foo when it is called as foo (513, 2)?

Consider the following recursive C function that takes two arguments:

unsigned int foo (unsigned int n, unsigned int r) {
  if (n > 0) return((n % r) + foo(n/r, r));
  else return 0;
}

What is the return value of the function foo when it is called as foo (345, 10)?

A company need to develop digital signal processing software for one of its newest inventions. The software is expected to have $$4000$$ lines of code. The company needs to determine the effort in person months needed to develop this software using basic $$COCOMO$$ model. The multiplicative factor for this model is given as $$2.8$$ for the software development on embedded systems. While the exponentiation factor is given as $$1.20.$$ What is the estimated effort in person months?

Which of the following is NOT desired in a good Software Requirement Specifications $$(SRS)$$ document?

A company needs to develop a strategy for Software Product development for which it has a choice of two programming language $${L_1}$$ and $${L_2}$$. The number of lines of code $$(LOC)$$ developed using $${L_2}$$ is estimated to be twice the $$LOC$$ developed with $${L_1}$$ the product will have to be maintained for five years. Various parameters for the company are given in the table below.

Total cost of the project includes cost of development & maintenance. What is the $$LOC$$ for $${L_1}$$ for which the cost of the project using $${L_1}$$ is equal to the cost of the project using $${L_2}$$

The following is comment written for $$a$$ $$c$$ function. This function computes the roots of quadratic equation. $$a{x^2} + bx + c = 0$$ the function stores two real roots in $${}^ * root1\,\,\& \,\,{}^ * root2\,\,\,\& $$ returns the status of validity of roots. In handles four different kinds of cases
$$i)$$ When coefficient $$a$$ is zero or irrespective of discriminate
$$ii)$$ When discriminate is positive.
$$iii)$$ When discriminate is zero
$$iv)$$ When discriminate is negative

Only in cases $$(ii)$$ & $$(iii)$$ the stored roots are valid Otherwise $$0$$ is stored in the roots the function returns $$0$$ when the roots are valid & - $$1$$ otherwise. The function also ensures root $$1$$ $$> =$$ root $$2.$$

int get QuadRoots(float a, float b, float c, float $${}^ * root1$$, float $${}^ * root2$$);

A software test engineer is assigned the job of doing block box testing. He comes up with the following test cases, many of which are redundant

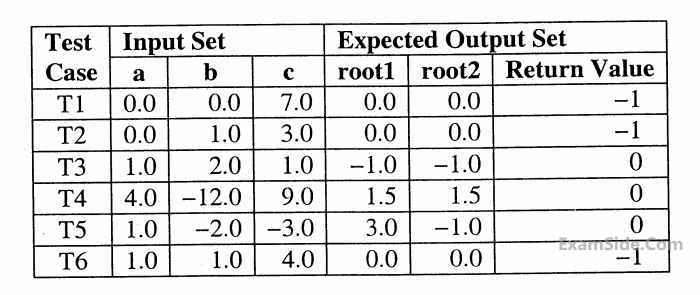
Which one of the following options provide the set of non-redundant tests using equivalence class partitioning approach from input perspective for black box testing?

Definition of the language $$L$$ with alphabet $$\left\{ a \right\}$$ is given as following. $$L = \left\{ {{a^{nk}}} \right.\left| {k > 0,\,n} \right.$$ is a positive integer constant$$\left. \, \right\}$$

What is the minimum number of states needed in a $$DFA$$ to recognize $$L$$?

The lexical analysis for a modern computer language such as java needs the power of which one of the following machine model in a necessary and sufficient sense?

Consider the languages $${L_1}$$, $${L_2}$$ and $${L_3}$$ are given below. $$$\eqalign{ & {L_1} = \left\{ {{0^p}{1^q}\left| {p,q \in N} \right.} \right\} \cr & {L_2} = \left\{ {{0^p}{1^q}\left| {p,q \in N} \right.\,\,and\,\,p = q} \right\}\,\,and \cr & {L_3} = \left\{ {{0^p}{1^q}{0^r}\left| {p,q,r\, \in N\,\,\,and\,\,\,p = q = r} \right.} \right\}. \cr} $$$

Which of the following statements is not TRUE?

A deterministic finite automation $$(DFA)$$ $$D$$ with alphabet $$\sum { = \left\{ {a,b} \right\}} $$ is given below

Which of the following finite state machines is a valid minimal $$DFA$$ which accepts the same languages as $$D?$$