Consider the Quicksort algorithm. Suppose there is a procedure for finding a pivot element which splits the list into two sub-lists each of which contains at least one-fifth of the elements. Let T(n) be the number of comparisons required to sort n elements. Then

We have a binary heap on n elements and wish to insert n more elements (not necessarily one after another) into this heap. The total time required for this is

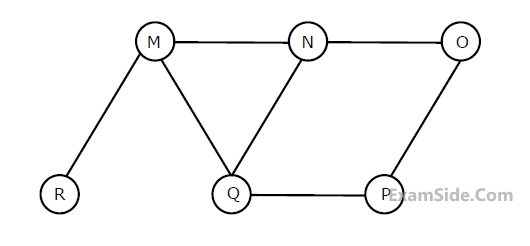
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is

Consider the following C functions:

int f1(int n){
 if(n == 0 || n == 1){
    return n;
 }
 return (2 * f1(n - 1) + 3 * f1(n - 2));
}
int f2(int n){
 int i;
 int X[N], Y[N], Z[N];
 X[0] = Y[0] = Z[0] = 0;
 X[1] = 1; Y[1] = 2; Z[1] = 3;
 for(i = 2; i <= n; i++){
  X[i] = Y[i - 1] + Z[i - 2];
  Y[i] = 2 * X[i];
  Z[i] = 3 * X[i];
 }
 return X[n];
}

The returning time of f1(n) and f2(n) are