There are 4 red, 5 green, and 6 blue balls inside a box. If 𝑁 number of balls are picked simultaneously, what is the smallest value of 𝑁 that guarantees there will be at least two balls of the same colour?
One cannot see the colour of the balls until they are picked.
Consider a circle with its centre at the origin (O), as shown. Two operations are allowed on the circle.
Operation 1: Scale independently along the x and y axes.
Operation 2: Rotation in any direction about the origin.
Which figure among the options can be achieved through a combination of these two operations on the given circle?

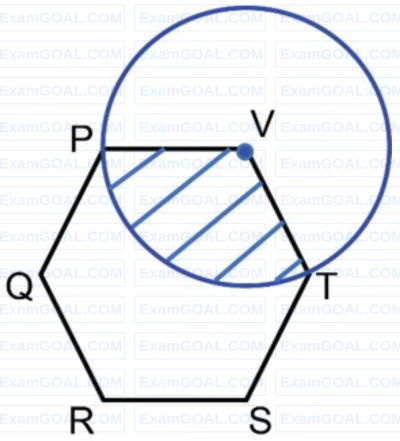
In the given figure, PQRSTV is a regular hexagon with each side of length 5 cm. A circle is drawn with its centre at V such that it passes through P. What is the area (in cm2 ) of the shaded region? (The diagram is representative)
An ant walks in a straight line on a plane leaving behind a trace of its movement. The initial position of the ant is at point P facing East.
The ant first turns 72$$^\circ$$ anticlockwise at P, and then does the following two steps in sequence exactly FIVE times before halting.

1. moves forward for 10 cm.
2. turns 144$$^\circ$$ clockwise
The pattern made by the trade left behind by the ant is







