In how many ways can cells in a 3 × 3 grid be shaded, such that each row and each column have exactly one shaded cell? An example of one valid shading is shown.

There are 4 red, 5 green, and 6 blue balls inside a box. If 𝑁 number of balls are picked simultaneously, what is the smallest value of 𝑁 that guarantees there will be at least two balls of the same colour?
One cannot see the colour of the balls until they are picked.
Consider a circle with its centre at the origin (O), as shown. Two operations are allowed on the circle.
Operation 1: Scale independently along the x and y axes.
Operation 2: Rotation in any direction about the origin.
Which figure among the options can be achieved through a combination of these two operations on the given circle?

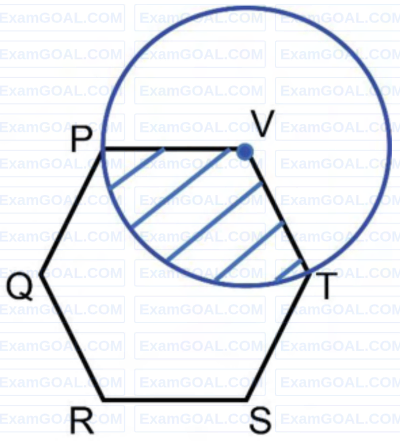
In the given figure, PQRSTV is a regular hexagon with each side of length 5 cm. A circle is drawn with its centre at V such that it passes through P. What is the area (in cm2 ) of the shaded region? (The diagram is representative)