The figure shows the single line diagram of a power system with a double circuit transmission line. The expression for electrical power is $$\,1.5\,\,\sin \delta ,\,\,$$ where $$\delta $$ is the rotor angle. The system is operating at the stable equilibrium point with mechanical power equal to $$1$$ pu. If one of the transmission line circuits is removed, the maximum value of $$\delta ,$$ as the rotor swings is $$1.221$$ radian. If the expression for electrical power with one transmission line circuit removed is $$\,{P_{\max }}\,\sin \delta ,\,\,$$ the valueof $${P_{\max }}\,,$$ in pu is _________.

The positive, negative and zero sequence reactances of a wye-connected synchronous generator are 0.2 pu, 0.2 pu, and 0.1 pu, respectively. The generator is on open circuit with a terminal voltage of 1 pu. The minimum value of the inductive reactance, in pu, required to be connected between neutral and ground so that the fault current does not exceed 3.75 pu if a single line to ground fault occurs at the terminals is _______ (assume fault impedance to be zero). (Give the answer up to one decimal place)

A $$3$$-bus power system is shown in the figure below, where the diagonal elements of $$Y$$-bus matrix are: $${Y_{11}} = - j12\,pu,\,\,\,{Y_{22}} = - j15\,pu\,\,$$ and $$\,{Y_{33}} = - j7\,pu.$$

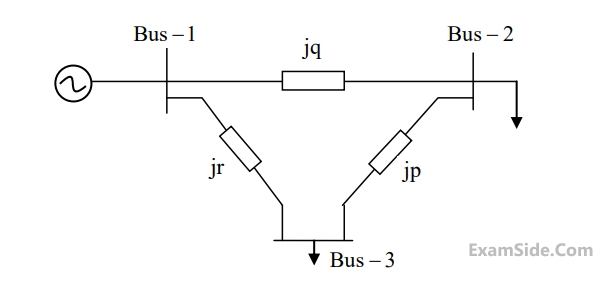
The per unit values of the line reactance's $$p, q$$ and $$r$$ shown in the figure are

Consider the system with following input-output relation $$y\left[n\right]=\left(1+\left(-1\right)^n\right)x\left[n\right]$$ where, x[n] is the input and y[n] is the output. The system is