An open loop transfer function $$G(s)$$ of system is $$G\left( s \right) = {k \over {s\left( {s + 1} \right)\left( {s + 2} \right)}}$$

For a unity feedback system, the breakaway point of the root loci on the real axis occurs at,

Nyquist plots of two functions $${G_1}\left( s \right)$$ and $${G_2}\left( s \right)$$ are shown in figure.

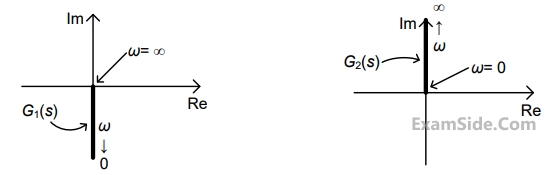
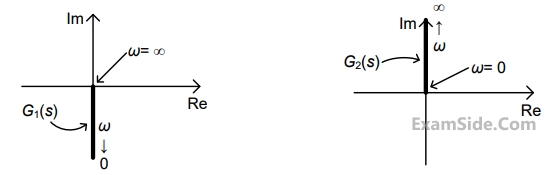
Nyquist plot of the product of $${G_1}\left( s \right)$$ and $${G_2}\left( s \right)$$ is

For the system governed by the set of equations: $$$\eqalign{ & d{x_1}/dt = 2{x_1} + {x_2} + u \cr & d{x_2}/dt = - 2{x_1} + u \cr & \,\,\,\,\,\,y = 3{x_1} \cr} $$$
the transfer function $$Y(s)/U(s)$$ is given by

Consider the following Sum of products expression, $$F.$$
$$F = ABC + \overline A \overline B C + A\overline B C + \overline A BC + \overline A \overline B \overline C $$

The equivalent Product of Sums expression is