The following discrete-time equations result from the numerical integration of the differential equations of an un-damped simple harmonic oscillator with state variables $$𝑥$$ and $$𝑦.$$ The integration time step is $$h.$$ $$${{{x_{k + 1}} - {x_k}} \over h} = {y_k},\,\,\,\,\,{{{y_{k + 1}} - {y_k}} \over h} = {x_k}$$$

For this discrete-time system, which one of the following statements is TRUE?

An open loop transfer function $$G(s)$$ of system is $$G\left( s \right) = {k \over {s\left( {s + 1} \right)\left( {s + 2} \right)}}$$

For a unity feedback system, the breakaway point of the root loci on the real axis occurs at,

Nyquist plots of two functions $${G_1}\left( s \right)$$ and $${G_2}\left( s \right)$$ are shown in figure.

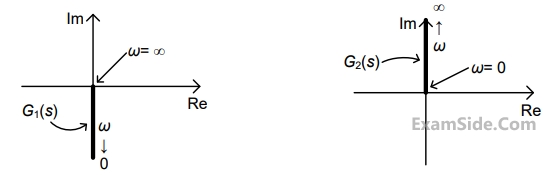
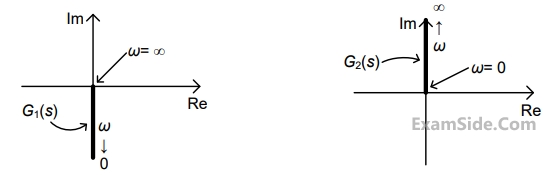
Nyquist plot of the product of $${G_1}\left( s \right)$$ and $${G_2}\left( s \right)$$ is

For the system governed by the set of equations: $$$\eqalign{ & d{x_1}/dt = 2{x_1} + {x_2} + u \cr & d{x_2}/dt = - 2{x_1} + u \cr & \,\,\,\,\,\,y = 3{x_1} \cr} $$$
the transfer function $$Y(s)/U(s)$$ is given by