1
GATE EE 2014 Set 2
Numerical
+1
-0
The sinusoidal ac source in the figure has an rms value of $${{20} \over {\sqrt 2 }}\,V.$$ Considering all possible values of $${R_L},\,\,$$ the minimum value of $${R_s}$$ in $$\Omega $$ to avoid burnout of the Zener diode is ______.
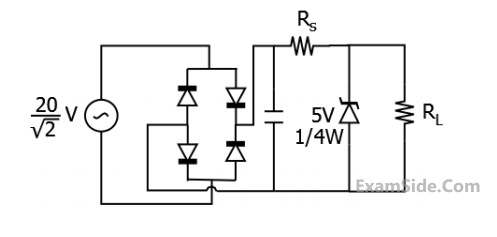

Your input ____
2
GATE EE 2014 Set 2
MCQ (Single Correct Answer)
+2
-0.6
Assuming the diodes to be ideal in the figure, for the output to be clipped, the input voltage $${V_i}$$ must be outside the range
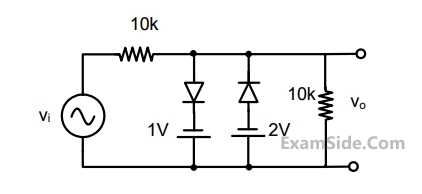

3
GATE EE 2014 Set 2
Numerical
+1
-0
The transistor in the given circuit should always be in active region. Take $${V_{CE\left( {sat} \right)}} = 0.2\,\,V,\,\,\,{V_{BE}} = 0.7\,\,V.\,\,\,$$ The maximum value of $${R_C}$$ in $$\Omega $$ which can be used, is __________.
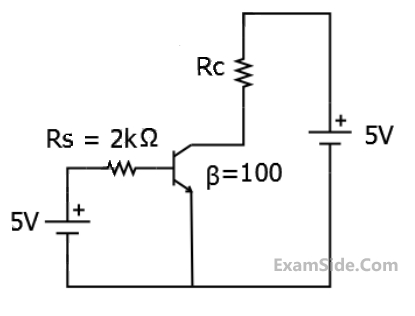

Your input ____
4
GATE EE 2014 Set 2
Numerical
+2
-0
An oscillator circuit using ideal op-amp and diodes is shown in the figure.
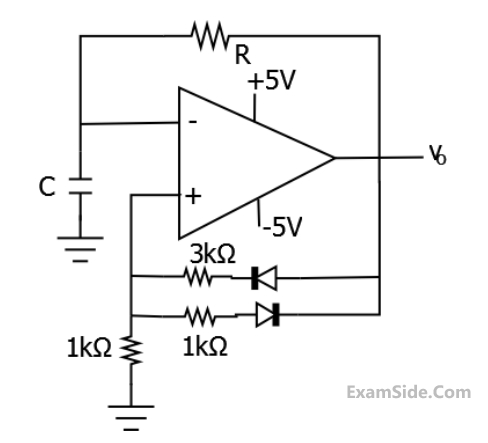

The duration for $$+ve$$ part of the cycle $$\Delta {t_1}$$ and for $$-ve$$ part is $$\Delta {t_2}.$$ The value of $$e$$ $${{\Delta {t_2} - \Delta {t_1}} \over {RC}}$$ will be _______.
Your input ____
Paper analysis
Total Questions
Analog Electronics
4
Control Systems
5
Digital Electronics
3
Electric Circuits
4
Electrical and Electronics Measurement
4
Electrical Machines
10
Electromagnetic Fields
2
Engineering Mathematics
8
Power Electronics
4
Power System Analysis
5
Signals and Systems
5
More papers of GATE EE
GATE EE 2025
GATE EE 2024
GATE EE 2023
GATE EE 2022
GATE EE 2021
GATE EE 2020
GATE EE 2019
GATE EE 2018
GATE EE 2017 Set 1
GATE EE 2017 Set 2
GATE EE 2016 Set 2
GATE EE 2016 Set 1
GATE EE 2015 Set 1
GATE EE 2015 Set 2
GATE EE 2014 Set 3
GATE EE 2014 Set 2
GATE EE 2014 Set 1
GATE EE 2013
GATE EE 2012
GATE EE 2011
GATE EE 2010
GATE EE 2009
GATE EE 2008
GATE EE 2007
GATE EE 2006
GATE EE 2005
GATE EE 2004
GATE EE 2003
GATE EE 2002
GATE EE 2001
GATE EE 2000
GATE EE 1999
GATE EE 1998
GATE EE 1997
GATE EE 1996
GATE EE 1995
GATE EE 1994
GATE EE 1993
GATE EE 1992
GATE EE 1991
GATE EE
Papers
2025
2024
2023
2022
2021
2020
2019
2018
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991