Given the characteristic equation $${s^3} + 2{s^2} + Ks + K = 0.$$ Sketch the root focus as $$K$$ varies from zero to infinity. Find the angle and real axis intercept of the asymptotes, break-away / break-in points, and imaginary axis crossing points, if any

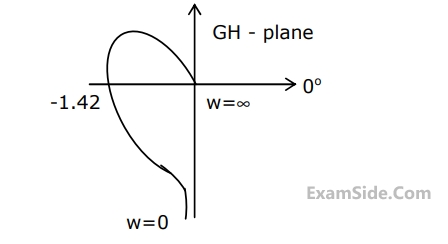
The polar plot of a type-$$1, 3$$-pole, open-loop system is shown in Fig. below. The closed loop system is

The asymptotic approximation of the log-magnitude versus frequency plot of a minimum phase system with real poles and one zero is shown in Fig. Its transfer functions is

A unity feedback system has an open-loop transfer function of $$G\left( s \right) = {{10000} \over {s{{\left( {s + 10} \right)}^2}}}$$
(a) Determine the magnitude of $$G\left( {j\omega } \right)$$ in dB at an angular frequency of $$\omega = 20rad/\sec .$$
(b) Determine the phase margin in degrees.
(c) Determine the gain margin in $$dB.$$
(d) Is the system stable or unstable?