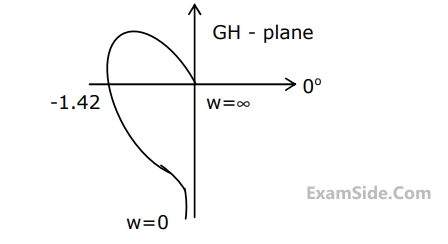
The polar plot of a type-$$1, 3$$-pole, open-loop system is shown in Fig. below. The closed loop system is

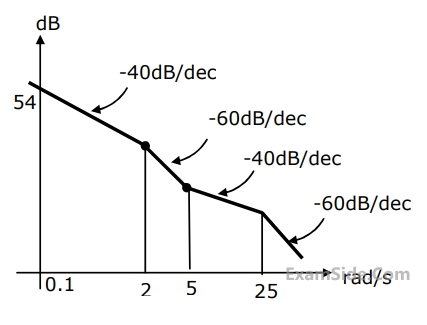
The asymptotic approximation of the log-magnitude versus frequency plot of a minimum phase system with real poles and one zero is shown in Fig. Its transfer functions is

A unity feedback system has an open-loop transfer function of $$G\left( s \right) = {{10000} \over {s{{\left( {s + 10} \right)}^2}}}$$
(a) Determine the magnitude of $$G\left( {j\omega } \right)$$ in dB at an angular frequency of $$\omega = 20rad/\sec .$$
(b) Determine the phase margin in degrees.
(c) Determine the gain margin in $$dB.$$
(d) Is the system stable or unstable?

Given the homogeneous state-space equation $$\mathop X\limits^ \bullet = \left[ {\matrix{ { - 3} & 1 \cr 0 & { - 2} \cr } } \right]x$$ the steady state value of $$\,\,{x_{ss}}\,\, = \mathop {Lim}\limits_{t \to \infty } x\left( t \right),$$ given the initial state value of $$x\left( 0 \right) = {\left[ {10 - 10} \right]^T},\,\,is$$