1
Consider the following C-program fragment in which i, j and n are integer variables.
for (i = n, j = 0; i > 0; i /= 2, j += i);
let val (j) denote the value stored in the variable j after termination of the for loop. Which one of the following is true?
2
An element in an array X is called a leader if it is greater than all elements to the
right of it in X. The best algorithm to find all leaders in an array
3
Let SHAM3 be the problem of finding a Hamiltonian cycle in a graph G = (V, E) with |V| divisible by 3 and DHAM3 be the problem of determining if a Hamiltonian cycle exists in such graphs. Which one of the following is true?
4
Let S be an NP-complete problem and Q and R be two other problems not known to be in NP. Q is polynomial time reducible to S and S is polynomial-time reducible to R. Which one of the following statements is true?
5
Consider the following graph:

Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
6
To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:
7
Consider a weighted complete graph G on the vertex set {v1, v2, ..vn} such that the weight of the edge (vi, vj) is $$2|i-j|$$. The weight of a minimum spanning tree of G is:
8
The median of n elements can be found in O(n) time. Which one of the following is correct about the complexity of quick sort, in which median is selected as pivot?
9
A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3
children. A 3-ary heap can be represented by an array as follows: The root is stored in
the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to
a[3]. The nodes from the second level of the tree from left to right are stored from a[4]
location onward. An item x can be inserted into a 3-ary heap containing n items by
placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Suppose the elements 7, 2, 10 and 4 are inserted, in that order, into the valid 3-
ary max heap found in the previous question. Which one of the following is
the sequence of items in the array representing the resultant heap?
10
Consider the following recurrence:
$$T\left( n \right){\rm{ }} = {\rm{ 2T(}}\left\lceil {\sqrt n } \right\rceil {\rm{) + }}\,{\rm{1 T(1) = 1}}$$
Which one of the following is true?
11
A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3
children. A 3-ary heap can be represented by an array as follows: The root is stored in
the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to
a[3]. The nodes from the second level of the tree from left to right are stored from a[4]
location onward. An item x can be inserted into a 3-ary heap containing n items by
placing x in the location a[n] and pushing it up the tree to satisfy the heap property.
Which one of the following is a valid sequence of elements in an array
representing 3-ary max heap?
12
Given two arrays of numbers a1,......,an and b1,......, bn where each number is 0 or 1,
the fastest algorithm to find the largest span (i, j) such that
ai+ai+1......aj = bi+bi+1......bj or report that there is not such span,
13
Which one of the following in place sorting algorithms needs the minimum
number of swaps?
14
In a binary max heap containing n numbers, the smallest element can be found
in time
15
Which one of the following grammars generates the following language?
$$L = \left( {{a^i}{b^j}|i \ne j} \right)$$
16
Consider the following grammar.
$$\eqalign{
& S \to S*E \cr
& S \to E \cr
& E \to F + E \cr
& E \to F \cr
& F \to id \cr} $$
Consider the following LR(0) items corresponding to the grammar above.
$$\eqalign{
& (i)\,S \to S*.E \cr
& (ii)\,E \to F. + E \cr
& (iii)\,E \to F + .E \cr} $$
Given the items above, which two of them will appear in the same set in the canonical sets-of-items for the grammar?
17
In the correct grammar of the previous question, what is the length of the derivation (number of steps starring from S) to generate the string $${a^l}{b^m}$$ with $$l \ne m$$?
18
Consider the following C code segment.
for (i = 0; i < n; i++)
{
for (j=0; j < n; j++)
{
if (i%2)
{
x += (4*j + 5*i);
y += (7 + 4*j);
}
}
}
Which one of the following is
false?
19
Consider the following translation scheme.
$$\eqalign{
& S \to ER \cr
& R \to *E\left\{ {pr{\mathop{\rm int}} ('*');} \right\}R\,|\,\varepsilon \cr
& E \to F + E\left\{ {pr{\mathop{\rm int}} (' + ');} \right\}\,|\,F \cr
& F \to S\,|\,id\,\left\{ {pr{\mathop{\rm int}} (id.value);} \right\} \cr} $$
Here id is a token that represents an integer and id.value represents the corresponding integer value. For an input '2 * 3 + 4' this translation scheme prints
20
Consider the following grammar:
$$\eqalign{
& S \to FR \cr
& R \to *S\,|\,\varepsilon \cr
& F \to id \cr} $$
In the predictive parser table, M, of the grammar the entries $$M\left[ {S,id} \right]$$ and $$M\left[ {R,\$ } \right]$$ respectively.
21
Consider the diagram shown below where a number of LANs are connected by (transparent) bridges. In order to avoid packets looping through circuits in the graph, the bridges organize themselves in a spanning tree. First, the root bridge is identified as the bridge with the least serial number. Next, the root sends out (one or more) data units to enable the setting up of the spanning tree of shortest paths from the root bridge to each bridge. Each bridge identifies a port (the root port) through which it will forward frames to the root bridge. Port conflicts are always resolved in favour of the port with the lower index value. When there is a possibility of multiple bridges forwarding to the same LAN (but not through the root port), ties are broken as follows: bridges closest to the root get preference and between such bridges, the one with the lowest serial number is preferred.

For the given connection of LANs by bridges, which one of the following choices represents the depth-first traversal of the spanning tree of bridges?
22
Two computers C1 and C2 are configured as follows. C1 has IP address 203.197.2.53 and netmask 255.255.128.0. C2 has IP address 203.197.75.201 and netmask 255.255.192.0. which one of the following statements is true?
23
For which one of the following reasons does Internet Protocol (IP) use the time-to-live (TTL) field in the IP datagram header?
24
Station A uses 32 byte packets to transmit messages to Station B using a sliding window protocol. The round trip delay between A and B is 80 milliseconds and the bottleneck bandwidth on the path between A and B is 128 kbps. What is the optimal window size that A should use?
25
Station A needs to send a message consisting of 9 packets to Station B using a sliding window (window size 3) and go-back-n error control strategy. All packets are ready and immediately available for transmission. If every 5th packet that A transmits gets lost (but no acks from B ever get lost), then what is the number of packets that A will transmit for sending the message to B?
26
Consider the diagram shown below where a number of LANs are connected by (transparent) bridges. In order to avoid packets looping through circuits in the graph, the bridges organize themselves in a spanning tree. First, the root bridge is identified as the bridge with the least serial number. Next, the root sends out (one or more) data units to enable the setting up of the spanning tree of shortest paths from the root bridge to each bridge. Each bridge identifies a port (the root port) through which it will forward frames to the root bridge. Port conflicts are always resolved in favour of the port with the lower index value. When there is a possibility of multiple bridges forwarding to the same LAN (but not through the root port), ties are broken as follows: bridges closest to the root get preference and between such bridges, the one with the lowest serial number is preferred.

Consider the correct spanning tree for the previous question. Let host H1 send out a broadcast ping packet. Which of the following options represents the correct forwarding table on B3?
27
Consider the following program segment. Here R1, R2 and R3 are the general purpose registers.

Assume that the content of memory location $$3000$$ is $$10$$ and the content of the register $$R3$$ is $$2000$$. The content of each of the memory locations from $$2000$$ to $$2010$$ is $$100.$$ The program is loaded from the memory location $$1000.$$ All the numbers are in decimal.
Assume that the memory is word addressable. The number of memory references for accessing the data in executing the program completely is
28
Consider the following program segment. Here R1, R2 and R3 are the general purpose registers.

Assume that the content of memory location $$3000$$ is $$10$$ and the content of the register $$R3$$ is $$2000$$. The content of each of the memory locations from $$2000$$ to $$2010$$ is $$100.$$ The program is loaded from the memory location $$1000.$$ All the numbers are in decimal.
Assume that the memory is word addressable. After the execution of this program, the content of memory location $$2010$$ is
29
Consider the following program segment. Here R1, R2 and R3 are the general purpose registers.

Assume that the content of memory location $$3000$$ is $$10$$ and the content of the register $$R3$$ is $$2000$$. The content of each of the memory locations from $$2000$$ to $$2010$$ is $$100.$$ The program is loaded from the memory location $$1000.$$ All the numbers are in decimal.
Assume that the memory is byte addressable and the word size is $$32$$ bits. If an interrupt occurs during the execution of the instruction $$''INC$$ $$R3'',$$ what return address will be pushed on to the stack?
30
A $$CPU$$ has $$24$$-bit instructions. A program starts at address $$300$$ (in decimal). Which one of the following is a legal program counter (all values in decimal)?
31
A CPU has five stages pipeline and runs at $$1$$ $$GHz$$ frequency. Instruction fetch happens in the first stage of the pipeline. A conditional branch instruction computes the target address and evaluates the condition in the third stage of the pipeline. The processor stops fetching new instruction following a conditional branch until the branch outcome is known. A program executes $${10^9}$$ instructions out of which $$20$$% are conditional branches. If each instruction takes one cycle to complete on average, then total execution time of the program is
32
Consider two cache organization: The first one is $$32$$ $$KB$$ $$2$$-way set associate with $$32$$-byte block size. The second one is of the same size but direct mapped. The size of an address is $$32$$ bits in both cases. $$A$$ $$2$$-to-$$1$$ multiplexer has latency. of $$0.6$$ $$ns$$ while a $$k$$-bit comparator has a latency of $$k/10$$ $$ns.$$ The bit latency of the set associative organization is $${h_1}$$ while that of the direct mapped one is $${h_2}.$$
The value of $${h_2}$$ is
33
A $$CPU$$ has a cache with block size $$64$$ bytes. The main memory has $$k$$ banks, each bank being $$c$$ bytes wide. Consecutive $$c$$-byte chunks are mapped on consecutive banks with wrap-around. All the $$k$$ banks can be accessed in parallel, but two accesses to the same bank must be serialized. A cache block access may involve multiple iterations of parallel bank accesses depending on the amount of data obtained by accessing all the $$k$$ banks in parallel. Each iteration requires decoding the bank numbers to be accessed in parallel and this takes $$k/2$$ $$ns.$$ The latency of one bank access is $$80$$ $$ns.$$ If $$c=2$$ and $$k=24,$$ then latency of retrieving a cache block starting at address zero from main memory is
34
Consider two cache organization: The first one is $$32$$ $$KB$$ $$2$$-way set associate with $$32$$-byte block size. The second one is of the same size but direct mapped. The size of an address is $$32$$ bits in both cases. $$A$$ $$2$$-to-$$1$$ multiplexer has latency. of $$0.6$$ $$ns$$ while a $$k$$-bit comparator has a latency of $$k/10$$ $$ns.$$ The bit latency of the set associative organization is $${h_1}$$ while that of the direct mapped one is $${h_2}.$$
The value of $${h_1}$$ is
35
Given two three bit number $${a_2}{a_1}{a_0}$$ and $${b_2}{b_1}{b_0}$$ and $$c,$$ the carry in the function that represents the carry generate function when these two numbers are added is
36
Let T be a depth first search tree in an undirected graph G. Vertices u and v are leaves of this tree T. The degrees of both u and v in G are at least 2. which one of the following statements is true?
37
Consider the depth-first-search of an undirected graph with 3 vertices P, Q, and R. Let discovery time d(u) represent the time instant when the vertex u is first visited, and finish time f(u) represent the time instant when the vertex u is last visited. Given that
d(P) = 5 units f(P) = 12 units
d(Q) = 6 units f(Q) = 10 units
d(R) = 14 unit f(R) = 18 units
Which one of the following statements is TRUE about the graph
38
Let T be a depth-first search tree in an undirected graph G. Vertices u and v are
leaves of this tree T. The degrees of both u and v in G are at least 2. Which one
of the following statements is true?
39
An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. If the root node is at level 0, the level of element X[i], i ≠ 0, is
40
An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. If only the root node does not satisfy the heap property, the algorithm to convert the complete binary tree into a heap has the best asymptotic time complexity of
41
An array X of n distinct integers is interpreted as a complete binary tree. The index of the first element of the array is 0. The index of the parent of element X[i],i≠0 is?
42
Which of the following sequences of array elements forms a heap?
43
Suppose that we have numbers between 1 and 100 in a binary search tree and want to search for the number 55. Which of the following sequences CANNOT be the sequence of nodes examined?
44
In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is
45
A scheme for storing binary trees in an array X is as follows. Indexing of X starts at 1 instead of 0. the root is stored at X[1]. For a node stored at X[i], the left child, if any, is stored in X[2i] and the right child, if any, in X[2i+1]. To be able to store any binary tree on n vertices the minimum size of X should be
46
The following function computes the value of
mC
n correctly for all legal values m and n (m≥1,n≥0 and m>n)
int func(int m, int n)
{
if (E) return 1;
else return(func(m -1, n) + func(m - 1, n - 1));
}
In the above function, which of the following is the correct expression for E?
47
An implementation of a queue Q, using two stacks S1 and S2, is given below:
void insert(Q, X){
push(S1, X);
}
void delete(Q){
if(stack - empty(S1)) then {
print("Q is empty");
return;
}else while (!(stack - empty(S1))){
X = pop(S1);
push(S2, X);
}
X = pop(S2);
}
Let n insert and $$m( \le n)$$ delete operations be performed in an arbitrary order on an empty queue Q. Let x and y be the number of push and pop operations performed respectively in the process. Which one of the following is true for all m and n?
48
Which of the following relational query languages have the same expressive power?
I) Relational algebra
II) Tuple relational calculus restricted to safe expressions
III) Domain relational calculus restricted to safe expressions
49
Consider the relations r1(P, Q, R) and r2(R, S, T) with primary keys P and R respectively. The relation r1 contains 2000 tuples and r2 contains 2500 tuples. The maximum size of the join $${r_1} \Join {r_2}$$ is
50
Consider a database with three relation instances shown below. The primary keys for the Drivers and Cars relation are Did and cid respectively and the records are stored in ascending order of these primary keys as given in the tables. No indexing is available in the database.
D: Drivers Relation
| Did |
Dname |
rating |
Age |
| 22 |
Karthikeyan |
7 |
25 |
| 29 |
Salman |
1 |
33 |
| 31 |
Boris |
8 |
55 |
| 32 |
Amoldt |
8 |
25 |
| 58 |
Schumacher |
10 |
35 |
| 64 |
Sachin |
7 |
35 |
| 71 |
Senna |
10 |
16 |
| 74 |
Sachin |
9 |
35 |
| 85 |
Rahul |
3 |
25 |
| 95 |
Ralph |
3 |
53 |
R: Reserves Relation
| Did |
cid |
Day |
| 22 |
101 |
10/10/06 |
| 22 |
102 |
10/10/06 |
| 22 |
103 |
8/10/06 |
| 22 |
104 |
7/10/06 |
| 31 |
102 |
10/11/06 |
| 31 |
103 |
6/11/06 |
| 31 |
104 |
12/11/06 |
| 64 |
101 |
5/9/06 |
| 64 |
102 |
8/9/06 |
| 74 |
103 |
8/9/06 |
C: Cars relation
| cid |
Cname |
Color |
| 101 |
Renault
|
Blue |
| 102 |
Renault
|
Red |
| 103 |
Ferrari |
Green |
| 104 |
Jaguar |
Red |
What is the output of the following SQL query?
Select D.dname
From Drivers D
Where D.did in (SELECT R.did
From Cars C,Reserves R
WHERE R.cid = C.cid and C.color = 'green')
51
Consider a database with three relation instances shown below. The primary keys for the Drivers and Cars relation are Did and cid respectively and the records are stored in ascending order of these primary keys as given in the tables. No indexing is available in the database.
D: Drivers Relation
| Did |
Dname |
rating |
Age |
| 22 |
Karthikeyan |
7 |
25 |
| 29 |
Salman |
1 |
33 |
| 31 |
Boris |
8 |
55 |
| 32 |
Amoldt |
8 |
25 |
| 58 |
Schumacher |
10 |
35 |
| 64 |
Sachin |
7 |
35 |
| 71 |
Senna |
10 |
16 |
| 74 |
Sachin |
9 |
35 |
| 85 |
Rahul |
3 |
25 |
| 95 |
Ralph |
3 |
53 |
R: Reserves Relation
| Did |
cid |
Day |
| 22 |
101 |
10/10/06 |
| 22 |
102 |
10/10/06 |
| 22 |
103 |
8/10/06 |
| 22 |
104 |
7/10/06 |
| 31 |
102 |
10/11/06 |
| 31 |
103 |
6/11/06 |
| 31 |
104 |
12/11/06 |
| 64 |
101 |
5/9/06 |
| 64 |
102 |
8/9/06 |
| 74 |
103 |
8/9/06 |
C: Cars relation
| cid |
Cname |
Color |
| 101 |
Renault
|
Blue |
| 102 |
Renault
|
Red |
| 103 |
Ferrari |
Green |
| 104 |
Jaguar |
Red |
Select D.dname
From Drivers D
Where D.did in (SELECT R.did
From Cars C,Reserves R
WHERE R.cid = C.cid and C.color = 'green')
Let n be the number of comparisons performed when the above SQL query is optimally executed. If linear search is used to locate a tuple in a relation using primary key, then n lies in the range
52
Consider the relation "enrolled (student, course)" in which (student, course) is the primary key, and the relation "paid (student, amount)" where student is the primary key. Assume no null values and no foreign keys or integrity constraints. Given the following four queries:
Query 1:
Select student
from enrolled
where student in (select student from paid)
Query 2:
Select student
from paid
where student in (select student from enrolled)
Query 3:
Select E.student
from enrolled E, paid P
where E.student = P.student
Query 4:
Select student
from paid
where exists (Select *
from enrolled
where enrolled.student = paid.student)
Which one of the following statements is correct?
53
Consider the relation
account (customer, balance) where customer is a primary key and there are no null values. We would like to rank customers according to decreasing balance. The customer with the largest balance gets rank 1. Ties are not broke but ranks are skipped: if exactly two customers have the largest balance they each get rank 1 and rank 2 is not assigned.
Query1:
Select A.customer, count(B.customer)
From account A, account B
Where A.balance <=B.balance
Group by A.customer
Query2:
Select A.customer, 1+count(B.customer)
From account A, account B
Where A.balance < B.balance
Group by A.customer
Consider these statements about Query1 and Query2.
1. Query1 will produce the same row set as Query2 for some but not all databases.
2. Both Query1 and Query2 are correct implementation of the specification
3. Query1 is a correct implementation of the specification but Query2 is not
4. Neither Query1 nor Query2 is a correct implementation of the specification
5. Assigning rank with a pure relational query takes less time than scanning in decreasing balance order assigning ranks using ODBC.
Which two of the above statements are correct?
54
The following functional dependencies are given :
$$\eqalign{
& AB \to CD,\,AF \to D,\,\,DE \to F, \cr
& C \to G.\,\,\,\,\,\,\,\,\,\,F \to E.\,\,\,\,\,\,\,\,\,G \to A. \cr} $$
Which one of the following options is false?
55
Consider the relation enrolled (student, course) in which (student, course ) is the primary key, and the relation Paid (student, amount) where student is the primary key. Assume no null values and no foreign keys or integrity constraints. Assume that amounts $$6000, 7000, 8000,9000$$ and $$10000$$ were each paid by $$20$$% of the students. Consider these query plans (Plan $$1$$ on left, Plan $$2$$ on right) to ''List all courses taken by students who have paid more than $$x''$$.


A disk seek takes $$4ms$$, disk data transfer bandwidth is $$300MB/s$$ and checking a tuple to see if amount is greater than $$x$$ takes $$10\mu s.$$ Which of the following statements is correct?
56
Consider the circuit in the diagram. The $$ \oplus $$ operator represents $$EX$$-$$OR.$$ The $$D$$ flip-flops are initialized to zeros (cleared).
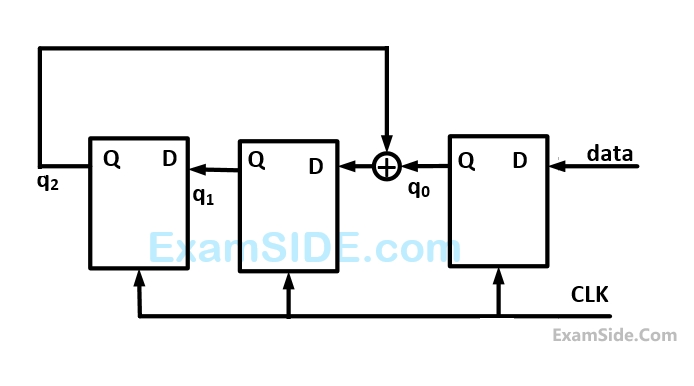
The following data: $$100110000$$ is supplied to the ''data'' terminal in nine clock cycles. After that the values of $${q_2}{q_1}{q_0}$$ are
57
You are given a free running clock with a duty cycle of $$50$$% and a digital waveform $$f$$ which changes only at the negative edge of the clock. Which one of the following circuits (using clocked $$D$$ flip-flops) will delay the phase of $$f$$ by $${180^0}?$$
58
Consider the circuit above. Which one of the following options correctly represents $$f(x,y,z)?$$

59
Consider a Boolean function $$f(w, x, y, z).$$ Suppose that exactly one of its inputs is allowed to change at a time. If the function happens to be true for two input vectors $${i_1} = < {w_1},{x_1},{y_1},{z_1} > $$ and $${i_2} = < {w_2},{x_2},{y_2},{z_2} > ,$$ we would like the function to remain true as the input changes from $${i_1}$$ to $${i_2}$$ ($${i_1}$$ and $${i_2}$$ differ in exactly one bit position), without becoming false momentarily. Let $$f\left( {w,x,y,z} \right) = \sum {\left( {5,7,11,12,13,15} \right)} .$$ Which of the following cube covers of $$f$$ will entire that the required property is satisfied?
60
Given a set of elements N = {1, 2, ....., n} and two arbitrary subsets $$A\, \subseteq \,N\,$$ and $$B\, \subseteq \,N\,$$, how many of the n! permutations $$\pi $$ from N to N satisfy $$\min \,\left( {\pi \,\left( A \right)} \right) = \min \,\left( {\pi \,\left( B \right)} \right)$$, where min (S) is the smallest integer in the set of integers S, and $${\pi \,\left( S \right)}$$ is the set of integers obtained by applying permutation $${\pi}$$ to each element of S?
61
What are the eigen values of the matrix $$P$$ given below?
$$$P = \left( {\matrix{
a & 1 & 0 \cr
1 & a & 1 \cr
0 & 1 & a \cr
} } \right)$$$
62
$$F$$ is an $$n$$ $$x$$ $$n$$ real matrix. $$b$$ is an $$n$$ $$x$$ $$1$$ real vector. Suppose there are two $$n$$ $$x$$ $$1$$ vectors, $$u$$ and $$v$$ such that $$u \ne v$$, and $$Fu = b,\,\,\,\,Fv = b$$
Which one of the following statements is false?
63
Consider the undirected graph $$G$$ defined as follows. The vertices of $$G$$ are bit strings of length $$n$$. We have an edge between vertex $$u$$ and vertex $$v$$ if and only if $$u$$ and $$v$$ differ in exactly one bit position (in other words, $$v$$ can be obtained from $$u$$ by flipping a single bit). The ratio of the choromatic number of $$G$$ to the diameter of $$G$$ is
64
The $${2^n}$$ vertices of a graph $$G$$ correspond to all subsets of a set of size $$n$$, for $$n \ge 6$$. Two vertices of $$G$$ are adjacent if and only if the corresponding sets intersect in exactly two elements.
The maximum degree of a vertex in $$G$$ is
65
The $${2^n}$$ vertices of a graph $$G$$ correspond to all subsets of a set of size $$n$$, for $$n \ge 6$$. Two vertices of $$G$$ are adjacent if and only if the corresponding sets intersect in exactly two elements.
the number of vertices of degree zero in $$G$$ is
66
What is the cardinality of the set of integers $$X$$ defined below?
$$X = $$ {$$n\left| {1 \le n \le 123,\,\,\,\,\,n} \right.$$ is not divisible by either $$2, 3$$ or $$5$$ }
67
For each elements in a set of size $$2n$$, an unbiased coin in tossed. The $$2n$$ coin tosses are independent. An element is chhoosen if the corresponding coin toss were head.The probability that exactly $$n$$ elements are chosen is
68
Consider the polynomial $$P\left( x \right) = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3},$$ where $${a_i} \ne 0,\forall i$$. The minimum number of multiplications needed to evaluate $$p$$ on an input $$x$$ is
69
Consider a weighted complete graph $$G$$ on the vertex set $$\left\{ {{v_1},\,\,\,{v_2},....,\,\,\,{v_n}} \right\}$$ such that the weight of the edge $$\left( {{v_i},\,\,\,\,{v_j}} \right)$$ is $$2\left| {i - j} \right|$$. The weight of a minimum spanning tree of $$G$$ is
70
If all the edge weights of an undirected graph are positive, then any subject of edges that connects all the vertices and has minimum total weight is a
71
Consider the set S = {a, b, c, d}. Consider the following 4 partitions $$\,{\pi _1},\,{\pi _2},\,{\pi _3},\,{\pi _4}$$ on $$S:\,{\pi _1} = \left\{ {\overline {a\,b\,c\,d} } \right\},\,{\pi _2} = \left\{ {\overline {a\,b\,} ,\,\overline {c\,d} } \right\},\,{\pi _3} = \left\{ {\overline {a\,b\,c\,} ,\,\overline d } \right\},\,{\pi _4} = \left\{ {\overline {a\,} ,\,\overline b ,\,\overline c ,\,\overline d } \right\}.$$ Let $$ \prec $$ be the partial order on the set of partitions $$S' = \{ {\pi _1},\,{\pi _2},\,{\pi _3},\,{\pi _4}\} $$ defined as follows: $${\pi _i} \prec \,\,{\pi _j}$$ if and only if $${\pi _i} $$ refines $${\pi _j}$$. The poset diagram for $$(S',\, \prec )$$ is
72
Let S = {1, 2, 3,....., m} , m > 3. Let $${X_1},\,....,\,{X_n}$$ be subsets of S each of size 3. Define a function f from S to the set of natural numbers as, f (i) is the number of sets $${X_j}$$ that contain the element i. That is $$f(i) = \left\{ {j\left| i \right.\,\, \in \,{X_j}} \right\}\left| . \right.$$
Then $$\sum\limits_{i - 1}^m {f\,(i)} $$ is
73
For the set $$N$$ of natural numbers and a binary operation $$f:N \times N \to N$$, an element $$z \in N$$ is called an identity for $$f$$ if $$f\left( {a,z} \right) = a = f\left( {z,a} \right)$$ for all $$a \in N$$. Which of the following binary operations have an identify?
$${\rm I}$$) $$\,\,\,\,\,\,f\left( {x,y} \right) = x + y - 3$$
$${\rm I}{\rm I}$$ $$\,\,\,\,\,\,f\left( {x,y} \right) = {\mkern 1mu} \max \left( {x,y} \right)$$
$${\rm I}{\rm I}{\rm I}$$$$\,\,\,\,\,f\left( {x,y} \right) = \,{x^y}$$
74
A relation $$R$$ is defined on ordered pairs of integers as follows:
$$\left( {x,y} \right)R\left( {u,v} \right)\,if\,x < u$$ and $$y > v$$. Then $$R$$ is
75
The set $$\left\{ {1,\,\,2,\,\,3,\,\,5,\,\,7,\,\,8,\,\,9} \right\}$$ under multiplication modulo 10 is not a group. Given below are four plausible reasons.
Which one of them is false?
76
Let $$X,. Y, Z$$ be sets of sizes $$x, y$$ and $$z$$ respectively. Let $$W = X x Y$$ and $$E$$ be the set of all subjects of $$W$$. The number of functions from $$Z$$ to $$E$$ is
77
Let E, F and G be finite sets.
Let $$X = \,\left( {E\, \cap \,F\,} \right)\, - \,\left( {F\, \cap \,G\,} \right)$$
and $$Y = \,\left( {E\, - \left( {E\, \cap \,G} \right)} \right)\, - \,\left( {E\, - \,F\,} \right)$$. Which one of the following is true?
78
Let $$P, Q$$, and $$R$$ be sets. Let $$\Delta $$ denote the symmetric difference operator defined as $$P\Delta Q = \left( {P \cup Q} \right) - \left( {P \cap Q} \right)$$. Using venn diagrams, determine which of the following is/are TRUE.
($${\rm I}$$) $$P\Delta \left( {Q \cap R} \right) = \left( {P\Delta Q} \right) \cap \left( {P\Delta R} \right)$$
($${\rm I}{\rm I}$$) $$P \cap \left( {Q\Delta R} \right) = \left( {P \cap Q} \right)\Delta \left( {P \cap R} \right)$$
79
Consider the following first order logic formula in which $$R$$ is a binary relation symbol.
$$\forall x\forall y\left( {R\left( {x,\,y} \right) \Rightarrow R\left( {y,x} \right)} \right).$$
The formula is
80
When a coin is tossed, the probability of getting a Head is p, 0 < p < 1. Let N be the random variable denoting the number of tosses till the first Head appears, including the toss where the Head appears. Assuming that successive tosses are indepandent, the expected value of N is
81
A logical binary relation $$ \odot $$, is defined as follows:

Let ~ be the unary negation (NOT) operator, with higher precedence then $$ \odot $$. Which one of the following is equivalent to $$A \wedge B?$$
82
In a certain town, the probability that it will rain in the afternoon is known to be 0.6. Moreover, meteorological data indicates that if the temperature at noon is less than or equal to $${25^ \circ }$$ C, the probability that it will rain in the afternoon is 0.4. The temperature at noon is equally likely to be above $${25^ \circ }$$ C, or at/below $${25^ \circ }$$ C. What is the probability that it will rain in the afternoon on a day when the temperature at noon is above $${25^ \circ }$$ C?
83
Consider the following propositional statements:
$${\rm P}1:\,\,\left( {\left( {A \wedge B} \right) \to C} \right) \equiv \left( {\left( {A \to C} \right) \wedge \left( {B \to C} \right)} \right)$$
$${\rm P}2:\,\,\left( {\left( {A \vee B} \right) \to C} \right) \equiv \left( {\left( {A \to C} \right) \vee \left( {B \to C} \right)} \right)$$ Which one of the following is true?
84
Which one of the first order predicate calculus statements given below correctly expresses the following English statement?
Tigers and lion attack if they are hungry of threatened.
85
A Computer system supports $$32$$-bit virtual addresses as well as $$32$$-bit physical addresses. Since the virtual address space is of the same size as the physical address space, the operating system designers decide to get rid of the virtual memory entirely. Which one of the following is true?
86
Consider the following snapshot of a system running n processes. Process i is
holding xi instances of a resource R, for $$1 \le i \le n$$. Currently, all instances of R are
occupied. Further, for all i, process i has placed a request for an additional
yi instances while holding the xi instances it already has. There are exactly two
processes p and q such that yp = yq = 0. Which one of the following can serve as
a necessary condition to guarantee that the system is not approaching a deadlock?
87
Barrier is a synchronization construct where a set of processes synchronizes globally i.e. each process in the set arrives at the barrier and waits for all others to arrive and then all processes leave the barrier. Let the number of processes in the set be three and S be a binary semaphore with the usual P and V functions. Consider the following C implementation of a barrier with line numbers shown on left.
void barrier (void) {
1: P(S);
2: process_arrived++;
3: V(S);
4: while (process_arrived !=3);
5: P(S);
6: process_left++;
7: if (process_left==3) {
8: process_arrived = 0;
9: process_left = 0;
10: }
11: V(S);
}
The variables process_arrived and process_left are shared among all processes and are initialized to zero. In a concurrent program all the three processes call the barrier function when they need to synchronize globally.
Which one of the following rectifies the problem in the implementation?
88
The atomic fetch-and-set x, y instruction unconditionally sets the memory location x to 1 and fetches the old value of x n y without allowing any intervening access to the memory location x. consider the following implementation of P and V functions on a binary semaphore S.
void P (binary_semaphore *s) {
unsigned y;
unsigned *x = &(s->value);
do {
fetch-and-set x, y;
} while (y);
}
void V (binary_semaphore *s) {
S->value = 0;
}
Which one of the following is true?
89
Barrier is a synchronization construct where a set of processes synchronizes globally i.e. each process in the set arrives at the barrier and waits for all others to arrive and then all processes leave the barrier. Let the number of processes in the set be three and S be a binary semaphore with the usual P and V functions. Consider the following C implementation of a barrier with line numbers shown on left.
void barrier (void) {
1: P(S);
2: process_arrived++;
3: V(S);
4: while (process_arrived !=3);
5: P(S);
6: process_left++;
7: if (process_left==3) {
8: process_arrived = 0;
9: process_left = 0;
10: }
11: V(S);
}
The variables process_arrived and process_left are shared among all processes and are initialized to zero. In a concurrent program all the three processes call the barrier function when they need to synchronize globally.
The above implementation of barrier is incorrect. Which one of the following is true?
90
Consider three processes, all arriving at time zero, with total execution time of $$10,20,$$ and $$30$$ units, respectively. Each process spends the first $$20$$% of execution time doing $${\rm I}/O$$, the next $$70$$% of time doing computation, and the last $$10$$% of time doing $${\rm I}/O$$ again. The operating system uses a shortest remaining compute time first scheduling algorithm and scheduling a new process either when the running processes gets blocked on $${\rm I}/O$$ or when the running process finishes its compute burst. Assume that all $${\rm I}/O$$ operations can be overlapped as much as possible. For what percentage of time does the $$CPU$$ remain idle?
91
Consider three processes (process id $$0,1,2,$$ respectively) with compute time bursts $$2, 4,$$ and $$8$$ time units. All processes arrive at time zero. Consider the longest remaining time first $$(LRTF)$$ scheduling algorithm. In $$LRTF$$ ties are broken by giving priority to the process with the lowest process id. The average turn around time is
92
Consider three $$CPU$$-intensive process, which require $$10,20$$ and $$30$$ time units and arrive at times $$0,2$$ and $$6$$ respectively. How many context switches are needed if the operating system implements a shortest remaining time first scheduling algorithm? Do not count the context switches at time zero and at the end.
93
Consider this C code to swap two integers and these five statements:
void swap(int *px, int *py)
{
*px = *px - *py;
*py = *px + *py;
*px = *py - *px;
}
S1: will generate a compilation error
S2: may generate a segmentation fault at runtime depending on the arguments passed
S3: correctly implements the swap procedure for all input pointers referring to integers stored in memory locations accessible to the process
S4: implements the swap procedure correctly for some but not all valid input pointers
S5: may add or subtract integers and pointers.
94
If $$s$$ is a string over $${\left( {0 + 1} \right)^ * }$$ then let $${n_0}\left( s \right)$$ denote the number of $$0'$$ s in $$s$$ and $${n_1}\left( s \right)$$ the number of $$1'$$s in $$s.$$ Which one of the following languages is not regular?
95
Let $${L_1}$$ be a regular language, $${L_2}$$ be a deterministic context-free language and $${L_3}$$ a recursively enumerable, but not recursive, language. Which one of the following statement is false?
96
For $$s \in {\left( {0 + 1} \right)^ * },$$ let $$d(s)$$ denote the decimal value of $$s(e. g.d(101)=5)$$
Let $$L = \left\{ {s \in {{\left( {0 + 1} \right)}^ * }\left| {\,d\left( s \right)\,} \right.} \right.$$ mod $$5=2$$ and $$d(s)$$ mod $$\left. {7 \ne 4} \right\}$$
Which of the following statement is true?
97
Consider the following statements about the context-free grammar
$$G = \left\{ {S \to SS,\,S \to ab,\,S \to ba,\,S \to \varepsilon } \right\}$$
$$1.$$ $$G$$ is ambiguous
$$2.$$ $$G$$ produces all strings with equal number of $$a's$$ and $$b's$$
$$3.$$ $$G$$ can be accepted by a deterministic $$PDA$$.
Which combination below expresses all the true statements about $$G?$$
98
Let $${L_1} = \left\{ {{0^{n + m}}{1^n}{0^m}\left| {n,m \ge 0} \right.} \right\},$$
$$\,\,\,{L_2} = \left\{ {{0^{n + m}}{1^{n + m}}{0^m}\left| {n,m \ge 0} \right.} \right\},$$ and
$$\,\,\,\,{L_3} = \left\{ {{0^{n + m}}{1^{n + m}}{0^{n + m}}\left| {n,m \ge 0} \right.} \right\},$$ Which of these languages are NOT context free?
99
Consider the regular language $$L = {\left( {111 + 11111} \right)^ * }.$$ The minimum number of states in any $$DFA$$ accepting this language is
 Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?  For the given connection of LANs by bridges, which one of the following choices represents the depth-first traversal of the spanning tree of bridges?
For the given connection of LANs by bridges, which one of the following choices represents the depth-first traversal of the spanning tree of bridges? Consider the correct spanning tree for the previous question. Let host H1 send out a broadcast ping packet. Which of the following options represents the correct forwarding table on B3?
Consider the correct spanning tree for the previous question. Let host H1 send out a broadcast ping packet. Which of the following options represents the correct forwarding table on B3?






