A single-input single-output feedback system has forward transfer function $$𝐺(𝑠)$$ and feedback transfer function $$𝐻(𝑠).$$ It is given that $$\left| {G\left( s \right)H\left( s \right)} \right| < 1.$$ Which of the following is true about the stability of the system?

The signal flow graph of a system is shown below. $$U(S)$$ is the input and $$C(S)$$ is the output.

Assuming $${h_1} = {b_1}$$ and $${h_0} = {b_0} - {b_1}{a_1},$$ the input-output transfer function, $$G\left( S \right) = {{C\left( S \right)} \over {U\left( S \right)}}$$ of the system is given by

The block diagram of a system is shown in the figure

If the desired transfer function of the system is $${{C\left( s \right)} \over {R\left( s \right)}}\, = {s \over {{s^2} + s + 1}},$$ then $$G(s)$$ is

The magnitude Bode plot of a network is shown in the figure

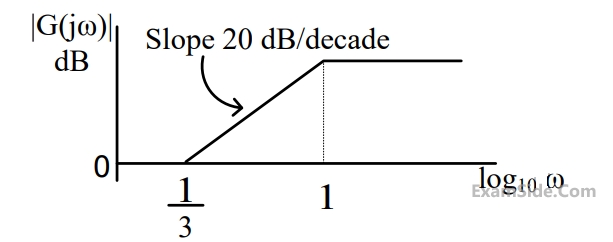
The maximum phase angle $${\phi _m}$$ and the corresponding gain $${G_m}$$ respectively are