GATE EE 2010 | GATE EE Year Wise Previous Years Questions

GATE EE 2010

MCQ (Single Correct Answer)

-0.6

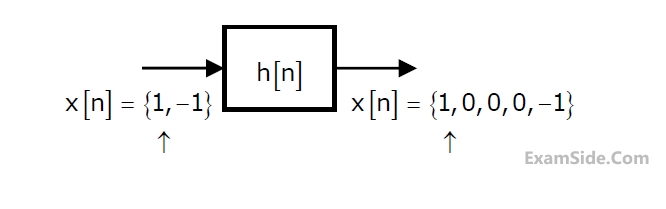
Given the finite length input x[n] and the corresponding finite length output y[n] of an LTI system as shown below, the impulse response h[n] of the system is GATE EE 2010 Signals and Systems - Linear Time Invariant Systems Question 30 English

GATE EE 2010 Signals and Systems - Linear Time Invariant Systems Question 30 English

$$\begin{array}{l}h\left[n\right]=\left\{1,\;0,\;0,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

$$\begin{array}{l}h\left[n\right]=\left\{1,\;0,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

$$\begin{array}{l}h\left[n\right]=\left\{1,\;1,\;1,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

$$\begin{array}{l}h\left[n\right]=\left\{1,\;1,\;1\right\}\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\uparrow\end{array}$$

GATE EE 2010

MCQ (Single Correct Answer)

-0.3

The system represented by the input-output relationship $$y\left(t\right)=\int_{-\infty}^{5t}x\left(\tau\right)d\tau$$, t > 0 is

Linear and causal

Linear but not causal

Causal but not linear

Neither linear nor causal

GATE EE 2010

MCQ (Single Correct Answer)

-0.3

The period of the signal $$x\left(t\right)=8\sin\left(0.8\mathrm{πt}+\frac{\mathrm\pi}4\right)$$ is

$$0.4\;\mathrm\pi\;\mathrm s$$

$$0.8\;\mathrm\pi\;\mathrm s$$

1.25 s

2.5 s

GATE EE 2010

MCQ (Single Correct Answer)

-0.3

The second harmonic component of the periodic waveform given in the figure has an amplitude of GATE EE 2010 Signals and Systems - Continuous Time Periodic Signal Fourier Series Question 20 English

GATE EE 2010 Signals and Systems - Continuous Time Periodic Signal Fourier Series Question 20 English

$$2/\mathrm\pi$$

$$\sqrt5$$

PREVIOUS NEXT

GATE EE Papers

2023