An electron in Hydrogen atom jumps from the second Bohr orbit to the ground state and the difference between the energies of the two states is radiated in the form of a photon. This photon strikes a material. If the work function of the material is 4.2 eV , then the stopping potential is (Energy of electron in $n$-th orbit $\left.=-\frac{13 \cdot 6}{n^2} \mathrm{eV}\right)$

The de-Broglie wavelength of a moving bus with speed $v$ is $\lambda$. Some passengers left the bus at a stoppage. Now when the bus moves with twice of its initial speed, its kinetic energy is found to be twice of its initial value. What is the de-Broglie wavelength of the bus now?

$10^{20}$ photons of wavelength 660 nm are emitted per second from a lamp. The wattage of the lamp is (Planck's constant $=6.6 \times 10^{-34} \mathrm{Js}$ )

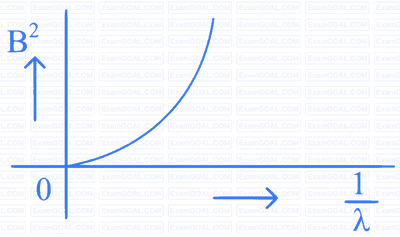
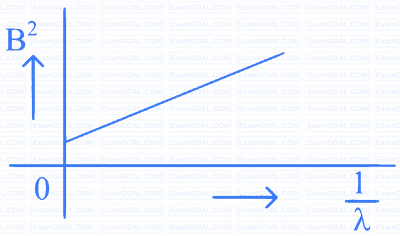
A beam of light of wavelength $$\lambda$$ falls on a metal having work function $$\phi$$ placed in a magnetic field B. The most energetic electrons, perpendicular to the field are bent in circular arcs of radius R. If the experiment is performed for different values of $$\lambda$$, then $$\mathrm{B}^2$$ vs. $$\frac{1}{\lambda}$$ graph will look like (keeping all other quantities constant)