If $x(t)$ satisfies the differential equation

$t \frac{dx}{dt} + (t - x) = 0$

subject to the condition $x(1) = 0$, then the value of $x(2)$ is __________ (rounded off to 2 decimal places).

Let $X$ be a continuous random variable defined on $[0, 1]$ such that its probability density function $f(x) = 1$ for $0 \leq x \leq 1$ and $0$ otherwise. Let $Y = \log_e (X + 1)$. Then the expected value of $Y$ is _____ . (rounded off to 2 decimal places)

A ram in the form of a rectangular body of size $l = 9 \text{ m}$ and $b = 2 \text{ m}$ is suspended by two parallel ropes of lengths $7 \text{ m}$. Assume the center-of-mass of the body is at its geometric center and $g = 9.81 \text{ m/s}^2$. For striking the object P with a horizontal velocity of $5 \text{ m/s}$, what is the angle $\theta$ with the vertical from which the ram should be released from rest?

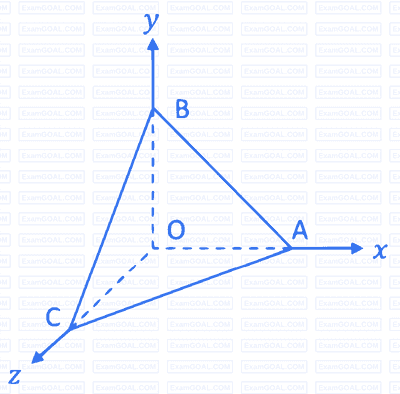
A rigid massless tetrahedron is placed such that vertex O is at the origin and the other three vertices A, B, and C lie on the coordinate axes as shown in the figure. The body is acted on by three point loads, of which one is acting at A along x-axis and another at point B along y-axis. For the body to be in equilibrium, the third point load acting at point O must be