A ram in the form of a rectangular body of size $l = 9 \text{ m}$ and $b = 2 \text{ m}$ is suspended by two parallel ropes of lengths $7 \text{ m}$. Assume the center-of-mass of the body is at its geometric center and $g = 9.81 \text{ m/s}^2$. For striking the object P with a horizontal velocity of $5 \text{ m/s}$, what is the angle $\theta$ with the vertical from which the ram should be released from rest?

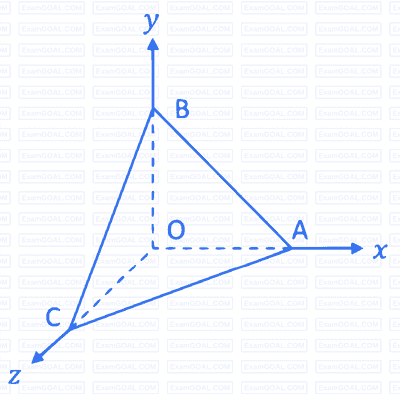
A rigid massless tetrahedron is placed such that vertex O is at the origin and the other three vertices A, B, and C lie on the coordinate axes as shown in the figure. The body is acted on by three point loads, of which one is acting at A along x-axis and another at point B along y-axis. For the body to be in equilibrium, the third point load acting at point O must be

A three-hinge arch ABC in the form of a semi-circle is shown in the figure. The arch is in static equilibrium under vertical loads of $P = 100$ kN and $Q = 50$ kN. Neglect friction at all the hinges. The magnitude of the horizontal reaction at B is _________ kN (rounded off to 1 decimal place).

The velocity field of a two-dimensional, incompressible flow is given by $\overrightarrow{V} = \ 2sin{h}\,x\,\hat{i} + v(x,y)\hat{j}$ where $ \hat{i}$ and $\underset{\dot{}}{j}$ denote the unit vectors in x and y directions, respectively. If $v(x, 0) = cosh\ x$, then $v(0,-1)$ is