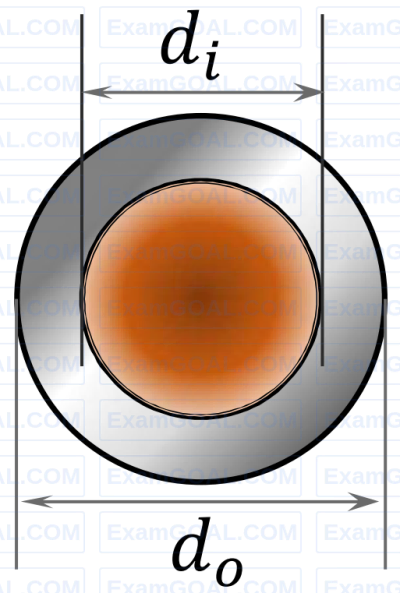
A shaft of length L is made of two materials, one in the inner core and the other in the outer rim, and the two are perfectly joined together (no slip at the interface) along the entire length of the shaft. The diameter of the inner core is d; and the external diameter of the rim is d₀, as shown in the figure. The modulus of rigidity of the core and rim materials are G_i and G₀, respectively. It is given that d₀ = 2d_i and G_i = 3G₀. When the shaft is twisted by application of a torque along the shaft axis, the maximum shear stress developed in the outer rim and the inner core turn out to be τ₀ and τ_i, respectively. All the deformations are in the elastic range and stress-strain relations are linear. Then the ratio τ_i/τ₀ is (round off to 2 decimal places).

For a dynamical system governed by the equation,

$\ddot{x}(t)+2 ζ \omega_n \dot{x}(t)+\omega_n^2x(t)=0$

the damping ratio ζ is equal to $\frac{1}{2\pi}\log_e2$. The displacement x of this system is measured during a hammer test. A displacement peak in the positive displacement direction is measured to be 4 mm. Neglecting higher powers (> 1) of the damping ratio, the displacement at the next peak in the positive direction will be _______ mm (in integer).

A spring mass damper system (mass m, stiffness k, and damping coefficient c) excited by a force F(t) = B sin ωt, where B, ω and t are the amplitude, frequency and time, respectively, is shown in the figure. Four different responses of the system (marked as (i) to (iv)) are shown just to the right of the system figure. In the figures of the responses, A is the amplitude of response shown in red color and the dashed lines indicate its envelope. The responses represent only the qualitative trend and those are not drawn to any specific scale.

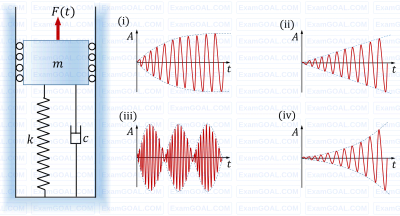
Four different parameter and forcing conditions are mentioned below.

(P) c > 0 and $ω=\sqrt{k/m}$

(Q) c < 0 and ω ≠ 0

(R) c = 0 and $\omega=\sqrt{k/m}$

(S) c = 0 and $\omega \cong\sqrt{k/m}$

Which one of the following options gives correct match (indicated by arrow →) of the parameter and forcing conditions to the responses?

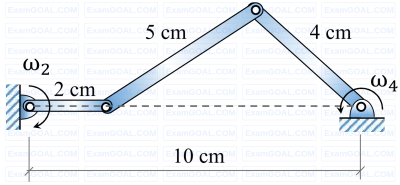
In the configuration of the planar four-bar mechanism at a certain instant as shown in the figure, the angular velocity of the 2 cm long link is ω₂ = 5 rad/s. Given the dimensions as shown, the magnitude of the angular velocity ω₄ of the 4 cm long link is given by rad/s (round off to 2 decimal places).