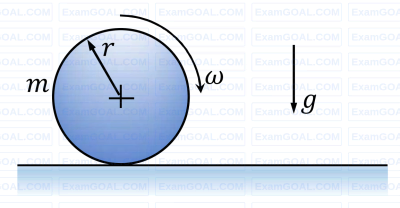
A cylindrical disc of mass m = 1 kg and radius r = 0.15 m was spinning at 𝜔 = 5 rad/s when it was placed on a flat horizontal surface and released (refer to the figure). Gravity g acts vertically downwards as shown in the figure. The coefficient of friction between the disc and the surface is finite and positive. Disregarding any other dissipation except that due to friction between the disc and the surface, the horizontal velocity of the center of the disc, when it starts rolling without slipping, will be _________ m/s (round off to 2 decimal places).

A tiny temperature probe is fully immersed in a flowing fluid and is moving with zero relative velocity with respect to the fluid. The velocity field in the fluid is $\vec V = (2x) \hat i + (y + 3t) \hat j,$ and the temperature field in the fluid is T = 2x² + xy + 4t, where x and y are the spatial coordinates, and t is the time. The time rate of change of temperature recorded by the probe at (x = 1, y = 1, t = 1) is _______.

In the following two-dimensional momentum equation for natural convection over a surface immersed in a quiescent fluid at temperature T_∞ (g is the gravitational acceleration, β is the volumetric thermal expansion coefficient, ν is the kinematic viscosity, u and v are the velocities in x and y directions, respectively, and T is the temperature)

$\rm u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = g β (T - T_∞) + \nu \frac{\partial^2 u}{\partial y^2} $

the term gβ(T - T_∞) represent

The figure shows a purely convergent nozzle with a steady, inviscid compressible flow of an ideal gas with constant thermophysical properties operating under choked condition. The exit plane shown in the figure is located within the nozzle. If the inlet pressure (P0) is increased while keeping the back pressure (Pback) unchanged, which of the following statements is/are true?