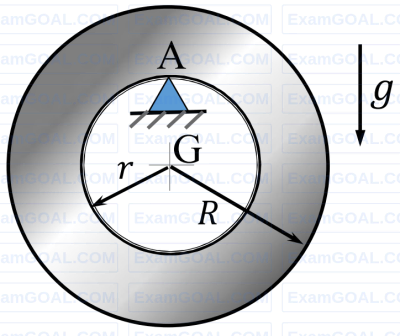
A rigid uniform annular disc is pivoted on a knife edge A in a uniform gravitational field as shown, such that it can execute small amplitude simple harmonic motion in the plane of the figure without slip at the pivot point. The inner radius r and outer radius 𝑅 are such that r² = R²/2, and the acceleration due to gravity is g. If the time period of small amplitude simple harmonic motion is given by $T = β π \sqrt{R/g} $ where π is the ratio of circumference to diameter of a circle, then β = ________ (round off to 2 decimal places).

A planar four-bar linkage mechanism with 3 revolute kinematic pairs and 1 prismatic kinematic pair is shown in the figure, where AB ⊥ CE and FD ⊥ CE. The T-shaped link CDEF is constructed such that the slider B can cross the point D, and CE is sufficiently long. For the given lengths as shown, the mechanism is

Consider a forced single degree-of-freedom system governed by $\rm \ddot x(t) + 2 ζ ω_n \dot x (t) + ω_n^2 x(t) = ω_n^2 \cos (ω t)$, where ζ and ω_n are the damping ratio and undamped natural frequency of the system, respectively, while ω is the forcing frequency. The amplitude of the forced steady state response of this system is given by [(1 − r²)² + (2ζr)²]^-1/2, where 𝑟 = ω/ωn. The peak amplitude of this response occurs at a frequency  ω =  ω_p. If  ω_d denotes the damped natural frequency of this system, which one of the following options is true?

A schematic of an epicyclic gear train is shown in the figure. The sun (gear 1) and planet (gear 2) are external, and the ring gear (gear 3) is internal. Gear 1, gear 3 and arm OP are pivoted to the ground at O. Gear 2 is carried on the arm OP via the pivot joint at P, and is in mesh with the other two gears. Gear 2 has 20 teeth and gear 3 has 80 teeth. If gear 1 is kept fixed at 0 rpm and gear 3 rotates at 900 rpm counter clockwise (ccw), the magnitude of angular velocity of arm OP is __________rpm (in integer).