The plane of the figure represents a horizontal plane. A thin rigid rod at rest is pivoted without friction about a fixed vertical axis passing through O. Its mass moment of inertia is equal to 0.1 kg∙cm2 about O. A point mass of 0.001 kg hits it normally at 200 cm/s at the location shown, and sticks to it. Immediately after the impact, the angular velocity of the rod is ___________ rad/s (in integer).

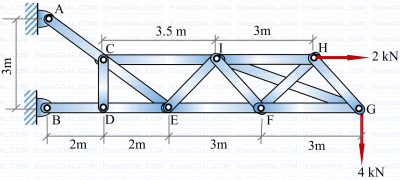
A structure, along with the loads applied on it, is shown in the figure. Self-weight of all the members is negligible and all the pin joints are friction-less. AE is a single member that contains pin C. Likewise, BE is a single member that contains pin D. Members GI and FH are overlapping rigid members. The magnitude of the force carried by member CI is ________ kN (in integer).

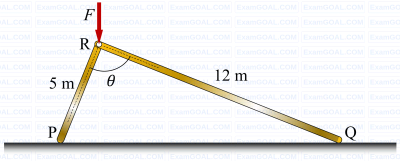
Two rigid massless rods PR and RQ are joined at frictionless pin-joint R and are resting on ground at P and Q, respectively, as shown in the figure. A vertical force F acts on the pin R as shown. When the included angle 𝜃 < 90°, the rods remain in static equilibrium due to Coulomb friction between the rods and ground at locations P and Q. At 𝜃 = 90°, impending slip occurs simultaneously at points P and Q. Then the ratio of the coefficient of friction at Q to that at P (μQ /μP) is _________ (round off to two decimal places).

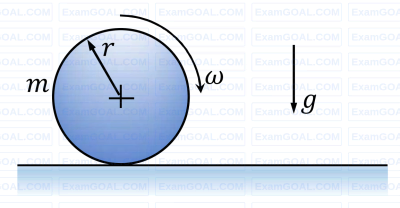
A cylindrical disc of mass m = 1 kg and radius r = 0.15 m was spinning at 𝜔 = 5 rad/s when it was placed on a flat horizontal surface and released (refer to the figure). Gravity g acts vertically downwards as shown in the figure. The coefficient of friction between the disc and the surface is finite and positive. Disregarding any other dissipation except that due to friction between the disc and the surface, the horizontal velocity of the center of the disc, when it starts rolling without slipping, will be _________ m/s (round off to 2 decimal places).