A set of $$5$$ jobs is to be processed on a single machine. The processing time (in days) is given in the table below. The holding cost for each job is Rs. $$K$$ per day.

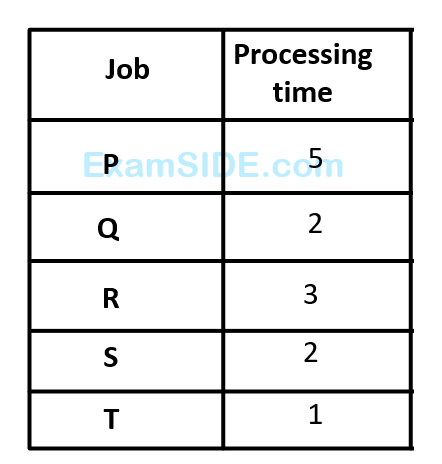
A schedule that minimizes the total inventory cost is

For the standard transportation linear programme with $$m$$ sources and $$n$$ destinations and total supply equaling total demand, an optimal solution (lowest cost) with the smallest number of non-zero $${X_{ij}}$$ values (amounts from source $$i$$ to destination $$j$$) is desired. The best upper bound for this number is

Consider the Linear programme $$(LP)$$
Max $$4x$$ + $$6y$$
Subject to
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,3x + 2y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,2x + 3y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,y \ge 0 \cr} $$

After introducing slack variables $$s$$ and $$t$$, the initial basic feasible solution is represented by the table below (basic variables are $$s=6$$ $$t=6,$$ and the objective function value is $$0$$).

After some simplex iterations, the following table is obtained

From this, one can conclude that

Consider the Linear programme $$(LP)$$
Max $$4x$$ + $$6y$$
Subject to
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,3x + 2y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,2x + 3y \le 6 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x,y \ge 0 \cr} $$

The dual for the $$LP$$ is