1
GATE ME 2008
MCQ (Single Correct Answer)
+2
-0.6
For the three dimensional object shown in the fig below. Five faces are insulated. The sixth face $$(PQRS),$$ which is not insulted, interacts thermally with the ambient , with a convective heat transfer coefficient of $$10W/{m^2}K.$$ The ambient temperature is $${30^ \circ }C$$. Heat is uniformly generated inside the object at the rate of $$100W/{m^3}.$$ Assuming the face $$PQRS$$ to be at uniform temperature, its steady state temp is


2
GATE ME 2008
MCQ (Single Correct Answer)
+2
-0.6
Steady two dimensional heat conduction takes place in the body shown in the fig below. The normal temperature gradients over surface $$P$$ and $$Q$$ can be considered to be uniform. The temperature gradient $$\partial T/\partial x = $$ at surface $$Q$$ is equal to $$10$$ $$K/m.$$ surfaces $$P$$ and $$Q$$ are maintained at constant temperatures as shown in the fig. While the remaining part of the boundary is insulated . The body has a constant thermal conductivity of $$0.1$$ $$W/mk$$, the value of $$\partial T/\partial x$$ and $$\partial T/\partial y$$ at surface $$P$$ are
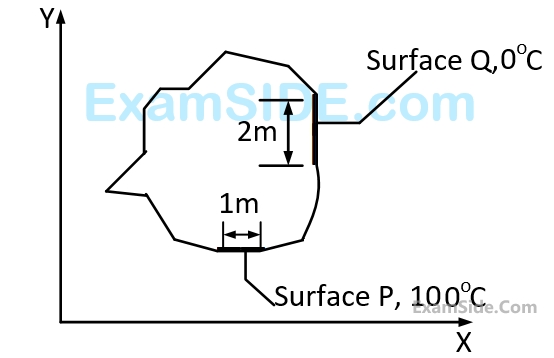

3
GATE ME 2008
MCQ (Single Correct Answer)
+2
-0.6
A set of $$5$$ jobs is to be processed on a single machine. The processing time (in days) is given in the table below. The holding cost for each job is Rs. $$K$$ per day.
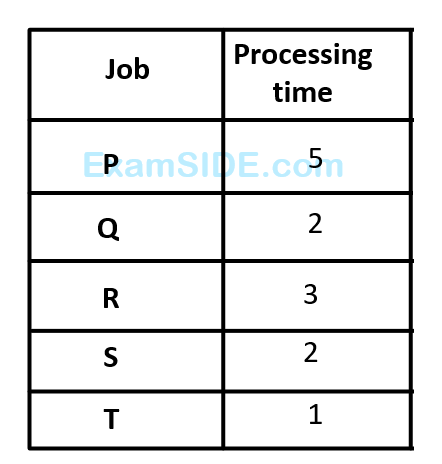

A schedule that minimizes the total inventory cost is
4
GATE ME 2008
MCQ (Single Correct Answer)
+2
-0.6
For the standard transportation linear programme with $$m$$ sources and $$n$$ destinations and total supply equaling total demand, an optimal solution (lowest cost) with the smallest number of non-zero $${X_{ij}}$$ values (amounts from source $$i$$ to destination $$j$$) is desired. The best upper bound for this number is
Paper analysis
Total Questions
Engineering Mathematics
15
Engineering Mechanics
3
Fluid Mechanics
6
Heat Transfer
5
Industrial Engineering
7
Machine Design
7
Production Engineering
13
Strength of Materials
9
Theory of Machines
3
Thermodynamics
10
Turbo Machinery
1
More papers of GATE ME
GATE ME 2025
GATE ME 2024
GATE ME 2023
GATE ME 2022 Set 2
GATE ME 2022 Set 1
GATE ME 2020 Set 2
GATE ME 2020 Set 1
GATE ME 2019 Set 1
GATE ME 2019 Set 2
GATE ME 2018 Set 2
GATE ME 2018 Set 1
GATE ME 2017 Set 2
GATE ME 2017 Set 1
GATE ME 2016 Set 1
GATE ME 2016 Set 3
GATE ME 2016 Set 2
GATE ME 2015 Set 2
GATE ME 2015 Set 1
GATE ME 2015 Set 3
GATE ME 2014 Set 1
GATE ME 2014 Set 4
GATE ME 2014 Set 2
GATE ME 2014 Set 3
GATE ME 2014 Set
GATE ME 2014
GATE ME 2013
GATE ME 2012
GATE ME 2011
GATE ME 2010
GATE ME 2009
GATE ME 2008
GATE ME 2007
GATE ME 2006
GATE ME 2005
GATE ME 2004
GATE ME 2003
GATE ME 2002
GATE ME 2001
GATE ME 2000
GATE ME 1999
GATE ME 1998
GATE ME 1997
GATE ME 1996
GATE ME 1995
GATE ME 1994
GATE ME 1993
GATE ME 1992
GATE ME 1991
GATE ME 1990
GATE ME 1989
GATE ME 1988
GATE ME 1987
GATE ME
Papers
2025
2024
2023
2014
2013
2012
2011
2010
2009
2008
2007
2006
2005
2004
2003
2002
2001
2000
1999
1998
1997
1996
1995
1994
1993
1992
1991
1990
1989
1988
1987