GATE ME
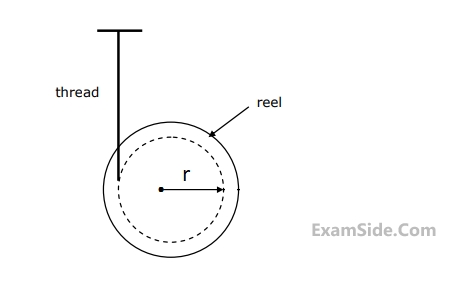
The tension in thread is

The linear acceletation of the reel is:

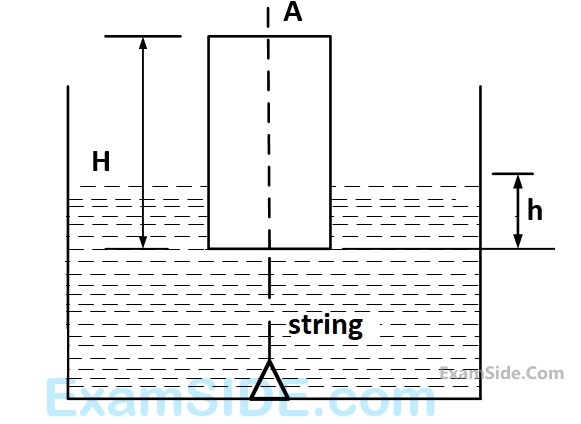
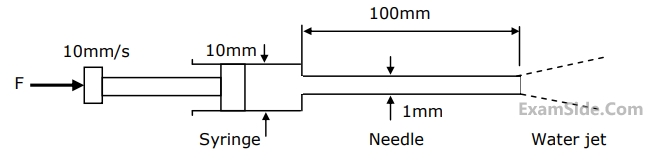
Assuming ideal flow, the force $$F$$ in Newton’s required on the plunger to push out the water is

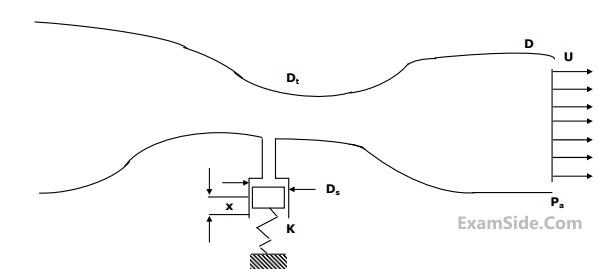
Neglect losses in the cylinder and assume fully developed laminar viscous flow throughout the needle; the Darcy friction factor is $${64/R_e}$$. Where $${R_e}$$ is the Reynolds number. Given that the viscosity of water is $$1.0 \times {10^{ - 3}}\,\,kg/m\,\,\,s,$$ the force $$F$$ in newtons required on the plunger is
The temperature and emissivity values for the surfaces of the room are $$300$$ $$K$$ and $$0.3$$ respectively. Boltzmannn constant $$\sigma = 5.67 \times {10^{ - 8}}\,\,W/{m^2}{K^4}.$$ The total heat loss from the two surfaces of the plate is
$$dT/dy = 1 \times {10^4}\,\,K/m.$$
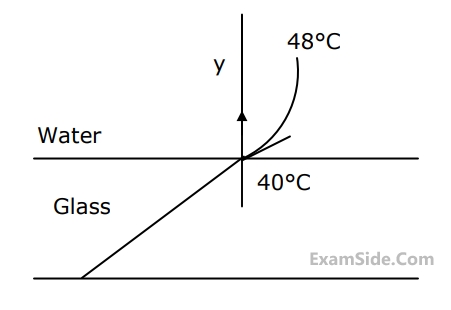
The heat transfer coefficient $$h$$ in $$W/{m^2}K$$ is
$$dT/dy = 1 \times {10^4}\,\,K/m...$$

The value of the temperature gradient in the glass at the water-glass interface in $$K/m$$ is
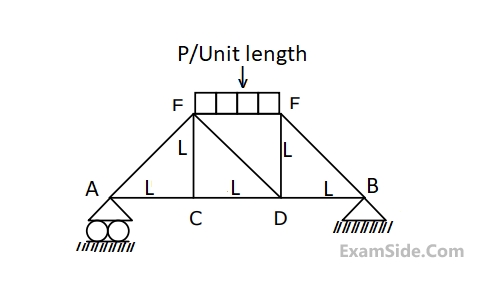
The maximum profit which can meet the constraints is
The project can be completed
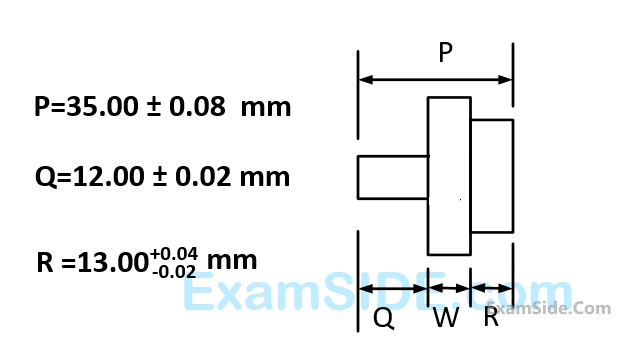
With $$100\% $$ confidence, the resultant dimension $$W$$ will have the specification
In the above problem, the coefficient of friction at the chip tool interface obtained using Earnest and Merchant theory is
The thickness of the produced chip is
The distance of maximum and minimum principal stresses at the point ''P'' from the Mohr's circle are
The maximum and minimum principal stresses respectively from the Mohr's circle are
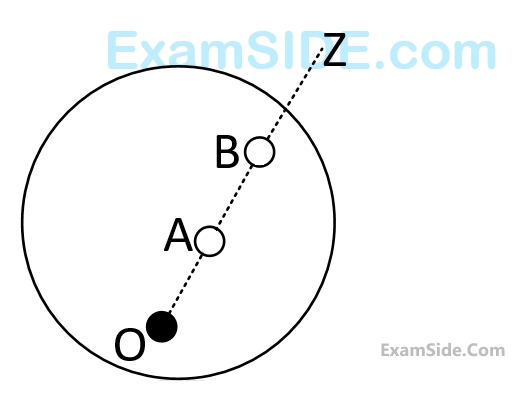
The acceleration of point $$B$$ with respect to point $$A$$ is a vector of magnitude

The velocity of point $$B$$ with respect to point $$A$$ is a vector of magnitude
Z2 and Z4 are
The centre distance in the second stage is
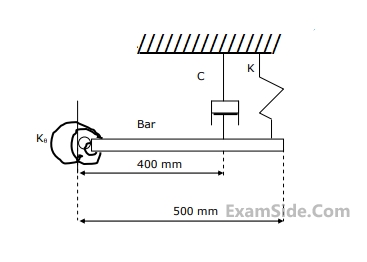
The un-damped natural frequency of oscillations of the bar about the hinge point is

The damping coefficient in the vibration equation is given by
The entropy change for the system during the process in $$kJ/K$$ is

The work interaction for the Nitrogen gas is
Which of the following statements is correct?