Consider a laminar boundary layer over a heated flat plate. The free stream velocity is $${U_\infty }.$$ At some distance $$x$$ from the leading edge the velocity boundary layer thickness is $${\delta _v}$$ and the thermal boundary layer is $${\delta _r}.$$ If the Prandtl number is greater than $$1,$$ then

Heat is being transferred by convection from water at $${48^ \circ }C$$ to a glass plate whose surface that is exposed to the water is at $${40^0}C.$$ The thermal conductivity of water is $$0.6$$ $$W/mK$$ and the thermal conductivity of glass is $$1.2$$ $$W/mK.$$ The spatial gradient of temp in the water at the water glass interface is
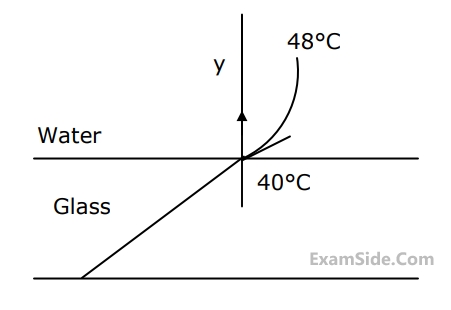
$$dT/dy = 1 \times {10^4}\,\,K/m.$$

The heat transfer coefficient $$h$$ in $$W/{m^2}K$$ is

Heat is being transferred by convection from water at $${48^ \circ }C$$ to a glass plate whose surface that is exposed to the water is at $${40^0}C.$$ The thermal conductivity of water is $$0.6$$ $$W/mK$$ and the thermal conductivity of glass is $$1.2$$ $$W/mK.$$ The spatial gradient of temp in the water at the water glass interface is
$$dT/dy = 1 \times {10^4}\,\,K/m...$$

The value of the temperature gradient in the glass at the water-glass interface in $$K/m$$ is

A manufacturer produces two types of products, $$1$$ and $$2,$$ at production levels of $${x_1}$$ and $${x_2}$$ respectively. The profit is given is$$2{x_1} + 5{x_2}.$$ The production constraints are $$$\eqalign{ & {x_1} + 3{x_2} \le 40 \cr & 3{x_1} + {x_2} \le 24 \cr & {x_1} + {x_2} \le 10 \cr & {x_1} > 0,\,{x_2} > 0 \cr} $$$

The maximum profit which can meet the constraints is