Metal Cutting · Machine Tools and Machining · GATE PI

A single point right handed turning tool is used for straight turning. The feed is $$0.25$$ $$mm/rev$$ and the uncut chip thickness is found to be $$0.25$$ $$mm.$$ The inclination angle of the main cutting edge is $${10^ \circ }.$$ The back rake angle (in degrees) is ________________

Built-up edge formation decreases under the conditions listed below EXCEPT

During turning of mild steel work material, the maximum temperature is observed at

The angle of a twist drill that determines its rake angle is

A spindle speed of $$300$$ $$rpm$$ and a feed $$0.3mm/revolution$$ are chosen for longitudinal turning operation on an engine lathe. In finishing pass, roughness on the work surface can be reduced by

Diamond cutting tools are not recommended for machining of ferrous metals due to

Diamond cutting tools are not recommended for machining of ferrous metals to

The cutting tool material normally used for turning steel of very high hardness is

If each abrasive grain is viewed as a cutting tool, then which of the following represents the cutting parameters in common grinding operations?

The effects of setting a boring tool above center height leads to a/an.

In metal cutting $$BUE$$ formation results in

Hot hardness is an essential property for

Only negative rake angles are used with the following tool materials

In $$HSS$$ Tool materials the element tungsten can be completely replaced, without changing the material property by

When the depth of cut is increased, the specific cutting energy

Machinability of steels is improved by the addition of

In metal cutting $$BUE$$ formation results in

Only negative rake angles are used with the following tool material

In metal cutting with a carbide tool, at the maximum recommended speed, the largest $$\% $$ of heat generated goes to the

Increase in rake angle causes ..........A................ in chip thickness and .............B......... in shear angle

(a) increase / reduction
(b) increase / decrease

Thrust force in drilling can be reduced by .................A............... the point angle and by ..........B.......... the helix angle of the drill

(a) increasing / reducing
(b) increasing / reducing

Amount of energy consumption for unit volume of metal removal is maximum in

$$BUE$$ formation ......A... the cutting force and ......B...... the surface finish

(a) decreases/ increases
(b) spoils / improves

In comparison to $$HSS$$, super $$HSS$$ contains higher percentage of

In $$HSS,$$ the tungsten can be substituted by

The Merchant circle diagram showing various forces associated with a cutting process using a wedge shaped tool is given in the Figure

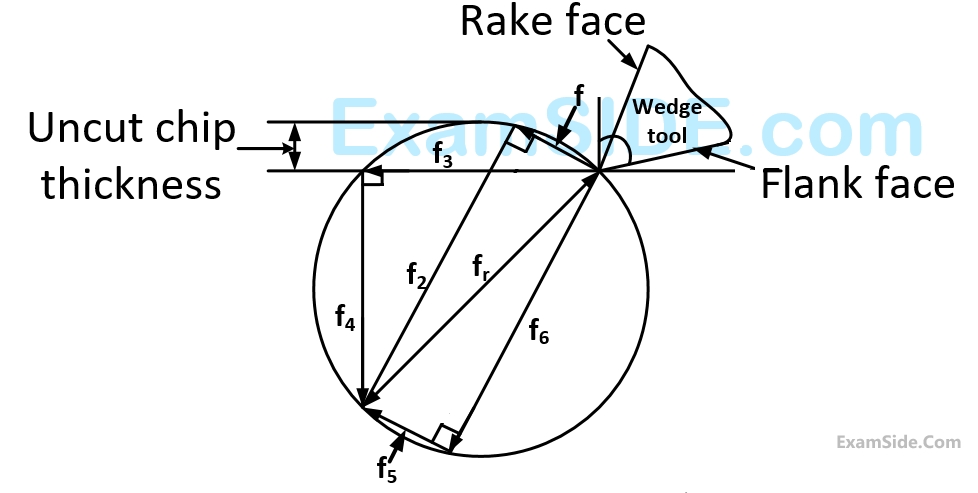
The coefficient of friction can be estimated from the ratio

In a machining operation with turning tool, the tool life $$(T)$$ is related to cutting speed $$v$$ $$(m/s),$$ feed $$f(mm)$$ and depth of cut $$d(mm)$$ as $$$T = C\,v{\,^{ - 2.5}}\,{f^{ - 0.9}}\,{d^{ - 0.15}}$$$
where, $$C$$ is a constant. The suggested values for the cutting parameters are: $$V=1.5$$ $$m/s,$$ $$f=0.25$$ $$mm$$ and $$d=3$$ $$mm$$ for normal rough turning. If the operation is performed at twice the cutting speed and the other parameters remain unchanged, the corresponding percentage change in tool life is ______________.

A $$60$$ $$mm$$ wide block of low carbon steel is face milled at a cutting speed of $$120$$ $$m/min,$$ feed of $$0.1$$ $$mm$$/tooth and axial depth of cut of $$4$$ $$mm.$$ A schematic representation of the face milling process is shown below. The diameter of the cutter is $$120$$ $$mm$$ and it has $$12$$ cutting edges. The material removal rate (in $$m{m^3}/s)$$ is __________

A cylindrical bar of $$100$$ $$mm$$ diameter is orthogonally straight turned with cutting velocity, feed and depth of cut of $$120$$ $$m/min$$, $$0.25$$ $$mm/rev$$ and $$4$$ $$mm,$$ respectively. The specific cutting energy of the work material is $$1 \times {10^9}\,\,J/{m^3}.$$ Neglect the contribution of feed force towards cutting power. The main or tangential cutting force (in $$N$$) is __________________

In an orthogonal machining experiment carried out using a cutting tool with zero degree rake angle, the measured cutting force was $$1700$$ $$N.$$ If the friction angle at the rake face-chip interface is $${26^ \circ },$$ then the thrust force value, in $$N$$ is ___________________

In orthogonal turning of a bar of $$100$$ $$mm$$ diameter with a feed of $$0.25$$ $$min/rev,$$ depth of cut of $$4$$ $$mm$$ and cutting velocity of $$90$$ $$m/min,$$ it is observed that the main (tangential) cutting force is prependicular to the friction force acting at the chip-tool interface. The main (tangential) cutting force is $$1500$$ $$N.$$

The normal force acting at the chip-tool interface in $$N$$ is

In orthogonal turning of a bar of $$100$$ $$mm$$ diameter with a feed of $$0.25$$ $$min/rev,$$ depth of cut of $$4$$ $$mm$$ and cutting velocity of $$90$$ $$m/min,$$ it is observed that the main (tangential) cutting force is prependicular to the friction force acting at the chip-tool interface. The main (tangential) cutting force is $$1500$$ $$N.$$

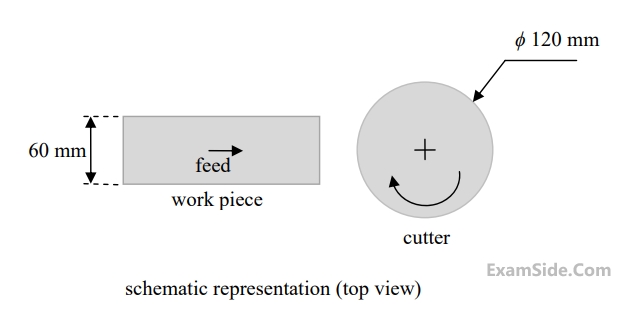
The orthogonal rake angle of the cutting tool in degree is

Following data refers to an automat and a center lathe, which are being compared to machine a batch of parts in a manufacturing shop

Automat will be economical if the batch size exceeds

Details pertaining to an orthogonal metal cutting process are given below.

Chip thickness ratio $$0.4$$
Under formed thickness $$0.6mm$$
Rake angle $$ + {10^0}$$
Cutting speed $$2.5m/s$$
Mean thickness of primary shear zone $$25microns$$

The shear strain rate in $${s^{ - 1}}$$ during the process is

Two cutting tools are being compared for a machining operation. The tool life equations are:
$$\eqalign{ & \,\,\,\,\,\,\,\,\,\,\,\,Carbi{\mathop{\rm de}\nolimits} \,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,V{T^{1.6}} = 3000 \cr & \,\,\,\,\,\,\,\,\,\,\,\,HSS\,\,tool:\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.6}} = 200 \cr} $$

Where $$V$$ is the cutting speed in $$m/min$$ and $$T$$ is the tool life in $$min.$$ The carbide tool will provide higher tool life if the cutting speed in $$m/min$$ exceeds

During turning of a low carbon steel bar with TiN coated carbide insert, one needs to improve surface finish without sacrificing material removal rate. To achieve improved surface finish one should

In an orthogonal machining operation , the tool life obtained is $$10min$$ at a cutting speed of $$10m/min,$$ while at $$75m/min$$ cutting speed, the tool life is $$30min$$. The value of index (n) in the Taylor's tool life equation is

An orthogonal operation is carried out at $$20m/min$$ cutting speed, using a cutting tool of rake angle $$15deg$$. The chip thickness is $$0.4mm$$ and uncut chip thickness is $$0.2mm.$$

The shear angle (in degrees) is

An orthogonal operation is carried out at $$20m/min$$ cutting speed, using a cutting tool of rake angle $$15deg$$. The chip thickness is $$0.4mm$$ and uncut chip thickness is $$0.2mm.$$

The chip velocity (in $$m/min$$) is

In an orthogonal cutting experiment, an $$HSS$$ tool having the following tool signature in the orthogonal reference system $$(ORS)$$ has been used: $$0-10-7-7-10-75-1$$
Given : Width of cut $$=3.6mm;$$
Shear strength of work piece material $$460N/m{m^2};$$
Depth of cut $$=0.25mm;$$
Coefficient of friction at chip tool interface $$=0.7.$$

Minimum Power requirement (in $$KW$$) at a cutting speed of $$150m/min$$ is

In an orthogonal cutting experiment, an $$HSS$$ tool having the following tool signature in the orthogonal reference system $$(ORS)$$ has been used: $$0-10-7-7-10-75-1$$
Given : Width of cut $$=3.6mm;$$
Shear strength of work piece material $$460N/m{m^2};$$
Depth of cut $$=0.25mm;$$
Coefficient of friction at chip tool interface $$=0.7.$$

Shear plane angle (in degrees) for minimum cutting force is

During machining, the wear land $$(h)$$ has been plotted against machining time $$(T)$$ as given in the following figure.

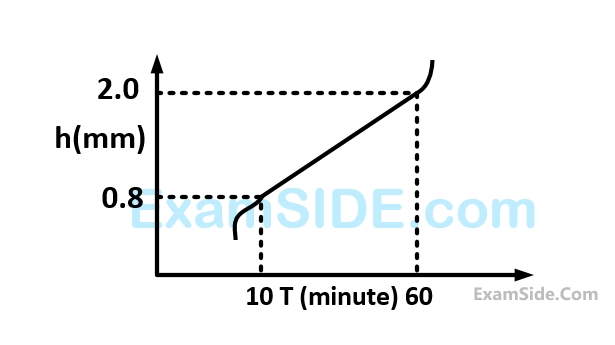
For a critical wear land of $$1.8mm,$$ the cutting tool life (in $$min$$) is

Brittle materials are machined with tools having zero or negative rake angles because it

In an orthogonal cutting test, the following observations were made
Cutting force $$=1200N ;$$ Thrust force $$=500N$$
Tool rake angle $$=zero ;$$ Cutting speed $$=1$$ $$m/s,$$
Depth of cut $$=0.8mm;$$
Chip thickness $$=1.5$$ $$mm$$

Chip speed along the tool rake face will be

In an orthogonal cutting test, the following observations were made
Cutting force $$=1200N ;$$ Thrust force $$=500N$$
Tool rake angle $$=zero ;$$ Cutting speed $$=1$$ $$m/s,$$
Depth of cut $$=0.8mm;$$
Chip thickness $$=1.5$$ $$mm$$

Friction angle during machining will be

The following data relate to an orthogonal turning process:
$$\,\,\,\,\,\,\,\,\,\,\,$$Back rake angle $$=15deg,$$
$$\,\,\,\,\,\,\,\,\,\,\,$$Width of cut $$=2mm,$$
$$\,\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$=0.4mm,$$
$$\,\,\,\,\,\,\,\,\,\,\,$$Feed rate $$=0.2mm/rev.$$

The shear angle is

Match List - $${\rm I}$$ with List - $${\rm I}$$$${\rm I}$$ and select the correct answer using the codes given below:

Match List - $${\rm I}$$ (Cutting tool materials) with List - $${\rm I}$$$${\rm I}$$ (Manufacturing methods) and select the correct answer using the codes given below the lists:

A batch of $$500$$ jobs of diameter $$50$$ $$mm$$ and length $$100$$ $$mm$$ is to be turned at $$200$$ $$rev/min$$ and feed $$0.2$$ $$mm/rev.$$

Applying Taylor's equation $$V{T^{0.25}} = 160,$$ the tool life in minutes is

A batch of $$500$$ jobs of diameter $$50$$ $$mm$$ and length $$100$$ $$mm$$ is to be turned at $$200$$ $$rev/min$$ and feed $$0.2$$ $$mm/rev.$$

The number of components per tool life

A $$\phi $$ $$40$$ $$mm$$ job is subjected to orthogonal turning by a $$ + {10^ \circ }$$ rake angle tool at $$500$$ $$rev/min.$$ By direct measurement during the cutting operation, the shear angle was found equal to $${25^ \circ }.$$

If the friction angle at the tool-chip interface is $${58^ \circ }$$ $$10'$$ and the cutting force components measured by a dynamometer are $$600$$ $$N$$ and $$200$$ $$N$$, the power loss due to friction (in $$kNm/min$$) is approximately

A $$\phi $$ $$40$$ $$mm$$ job is subjected to orthogonal turning by a $$ + {10^ \circ }$$ rake angle tool at $$500$$ $$rev/min.$$ By direct measurement during the cutting operation, the shear angle was found equal to $${25^ \circ }.$$

The velocity (in $$m/min$$) with which the chip flows on the tool face is

The following data relate to an orthogonal turning process:
$$\,\,\,\,\,\,\,\,\,\,\,$$Back rake angle $$=15deg,$$
$$\,\,\,\,\,\,\,\,\,\,\,$$Width of cut $$=2mm,$$
$$\,\,\,\,\,\,\,\,\,\,\,$$Chip thickness $$=0.4mm,$$
$$\,\,\,\,\,\,\,\,\,\,\,$$Feed rate $$=0.2mm/rev.$$

If the cutting force and the thrust force are $$900N$$ and $$810N,$$ the mean strength in $$Mpa$$

Consider the following statements
$$1.$$ $$\,\,\,\,\,\,\,\,\,\,\,\,$$ As the cutting speed increases, the cost of production initially reduces, then
$$\,\,\,\,\,\,\,\,\,\,\,\,$$after an optimum cutting speed it increases.
$$2.$$ $$\,\,\,\,\,\,\,\,\,\,\,\,$$ As the cutting speed increases the cost of production also increases and
$$\,\,\,\,\,\,\,\,\,\,\,\,$$after a critical value to it reduces.
$$3.$$ $$\,\,\,\,\,\,\,\,\,\,\,\,$$ Higher feed rate for the same cutting speed reduces cost of production.
$$4.$$ $$\,\,\,\,\,\,\,\,\,\,\,\,$$ Higher feed rate for the same cutting speed increases the cost of production

Which of the statements given above are correct?

The rake angle of a cutting tool is $${15^ \circ }$$, shear angle $${45^ \circ }$$ and cutting velocity $$35$$ $$m/min$$. What is the velocity of chip along the tool face?

Consider the following statements
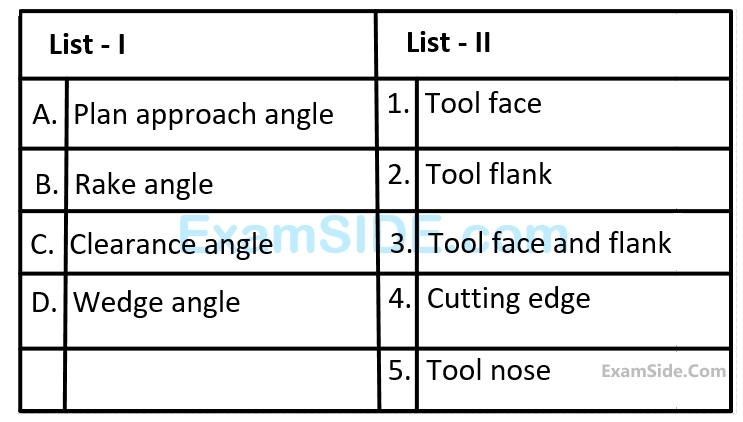
During the third stage of tool-wear, rapid deterioration of tool edge takes place because
$$1.$$ Flank wear is only marginal.
$$2.$$ Flank wear is large.
$$3.$$ Temperature of the tool increases gradually.
$$4.$$ Temperature of the tool increases drastically.

Which of the statements given above are correct?

In a machining operation chip thickness ratio is $$0.3$$ and the back rake angle of the tool is $${10^ \circ }.$$ What is the value of the shear strain?

Two identical cylindrical jobs are turned using (a) a round nosed tool of nose radius $$2$$ $$mm$$ and (b) a sharp corner tool having principal cutting edge angle $$ = {45^ \circ }$$ and auxiliary cutting edge angle $$ = {10^ \circ }$$. If the operation is carried out at a feed of $$0.08$$ $$mm/rev,$$ the heights of micro irregularities on the machined surfaces (in $$mm$$) in the two cases will be

Consider the following statements with respect to the relief angle of cutting tool:

$$1.$$ This affects the direction of chip flow.
$$2.$$ This reduces excessive friction between the tool and work piece
$$3.$$ This affects tool life
$$4.$$ This allows better access of coolant to the tool-work piece interface

Which of the statements given above are correct?

In which of the choices given below, the cutting tool materials are placed in the ascending order of permissible cutting speed for machining of steel?

A cylinder of $$25mm$$ diameter and $$100mm$$ length is turned with a tool, for which the relation $$V{T^{0.25}} = 55$$ is applicable. The cutting velocity is $$22m/min.$$ For a tool feed of $$0.046$$ $$mm/rev,$$ the number of tool regrinds required to produce $$425$$ cylinders is

A single point cutting tool with a nose radius of $$0.4$$ $$mm$$ was used to turn a component in a lathe employing a feed rate of $$0.3$$ $$mm/rev.$$ If the feed-rate is doubled, the ideal surface roughness (peak-to-valley height) produced on the component will increase by a factor of

Orthogonal machining of a steel work-piece is done with a $$HSS$$ tool of zero rake angle. The ratio of the cutting force and the thrust force on the tool is $$1:0.372.$$ The length of cut chip is $$4.71$$ $$mm$$ while the uncut chip length is $$10$$ $$mm.$$ What are the shear plane angle $$\phi $$ and friction angle $$\beta $$ in deg.? Use Merchant's theory.

Tool life equation for two tools under consideration are as follows

$$\eqalign{ & HSS:\,\,\,\,\,\,\,\,\,\,\,\,\,V{T^{0.2}} = 150 \cr & Carbide:\,\,\,\,\,\,V{T^{0.3}} = 250 \cr} $$
Where $$V$$ is the cutting speed in $$m/min$$ and $$T$$ is the tool life in $$min.$$ The breakdown cutting speed above which the carbide tool will be beneficial is

Two different tools $$A$$ and $$B$$ having nose radius of $$0.6mm$$ and $$0.33mm$$ respectively are used to machine $$C-45$$ steel employing feed rate of $$0.2$$ $$mm/rev$$ and $$0.1mm/rev$$ respectively. The tool that gives better finish and the value of ideal surface roughness are

A $$60deg$$ symmetrical $$V$$ tool is used in shaping a work piece with a depth of cut of $$0.1$$$$mm$$ and feed of $$0.1mm/stroke$$. The theoretical peak to valley height, in $$mm,$$ of the surface produced is

The heat generated in metal cutting is dissipated in different proportions into environment, tool, chip and work-piece. The correct order of this proportion in decreasing magnitude is (no cutting fluid is use ($$d$$)

In a cutting test with $$0.3mm$$ flank wear as tool failure criterion, a tool life of $$10min$$ was obtained at a cutting velocity of $$20m/min.$$ Taking tool life exponrent as $$0.25,$$ the tool life in minutes at $$40m/min$$ of cutting velocity will be

A single point cutting tool with $${12^0}$$ rake angle is used for orthogonal machining of a ductile material. The shear plane angle for the theoretically minimum possible shear strain to occur

The following data refers to an orthogonal machining of mild steel with a single point $$HSS$$ tool. Rake angle of tool $$ = {10^ \circ },$$ uncut chip thickness $$=0.3mm,$$ width of cut $$=2.0mm,$$ single plane shear angle $$ = {36^ \circ },$$ shear strength of mild steel $$=450$$ $$MPa,$$ using Merchants analysis

The coefficient of friction between the chip and tool will be

The following data refers to an orthogonal machining of mild steel with a single point $$HSS$$ tool. Rake angle of tool $$ = {10^ \circ },$$ uncut chip thickness $$=0.3mm,$$ width of cut $$=2.0mm,$$ single plane shear angle $$ = {36^ \circ },$$ shear strength of mild steel $$=450$$ $$MPa,$$ using Merchants analysis

The shear force in cutting will be

A cutting tool is designated in 'Orthogonal Rake System' as: $$${0^ \circ } - {0^ \circ } - {6^ \circ } - {6^ \circ } - {25^ \circ } - {75^ \circ } - 0.8\,\,mm.$$$
The following data were given
$${S_0} = $$ feed $$=0.12$$ $$mm/rev$$
$$T=$$ depth of cut $$=2.0$$ $$mm$$
$${a_2} = $$ chip thickness $$=0.22$$ $$mm$$
$${V_f} = $$ chip velocity $$=52.6$$ $$m/min$$
$${\tau _s} = $$ dynamic yield shear strength $$=400$$ $$MPa$$
$${P_z} = $$ main cutting force $$ = {S_0}\,t\,{\tau _s}\left( {\zeta \,\sec y - \tan \gamma + 1} \right)$$

Where $$\zeta = $$ chip reduction coefficient and $$\gamma = $$ orthogonal rake.
The main cutting force $$\left( {{P_z}} \right)$$ and cutting power assuming orthogonal machining are

Tool life in drilling steel using $$HSS$$ drill is expressed as $${T^{0.2}} = 9.8\,\,{D^{0.4}}\,\,/\,\,V\,{s^{0.5}}$$ where $$D$$ is the drill diameter (in $$mm$$), $$T$$ is the tool life (in minutes), $$V$$ is the cutting speed (in $$m/min$$) and $$s$$ is the feed ($$mm/rev$$). The feed is set at maximum possible value of $$0.4$$ $$mm/rev$$ for a given drill diameter of $$30mm.$$ The length of drilling is $$50mm.$$ The machine hour rate Rs $$60$$ and the cost of drill is Rs. $$400.$$

$$i)$$ For the given conditions, the tailor's exponent and constant are .............
$$ii)$$ The optimum cutting speed, $${V_{opt}},$$ neglecting the work-piece and tool changing times is

In certain machining operation with a cutting speed of $$50$$ $$m/min,$$ tool life of $$45$$ minutes was observed, when the cutting speed was increased to $$100$$ $$m/min,$$ the tool life decreased to $$10$$ minutes. The cutting speed for maximum productivity, if tool change time is $$2$$ minutes is

In an orthogonal machining experiment using a tool having $${6^ \circ }.$$ Rake angle, the following data were collected. Cutting speed $$0.5$$ $$m/sec,$$ width of cut $$3$$ $$mm,$$ depth of cut $$1mn,$$ chip thickness $$1.5mm.$$ Assuming that shearing takes place under minimum energy condition,

The coefficient of friction between the chip tool interfaces will be

In a single pass turning operation the cutting speed is the only variable Based on the cutting time cost and the cutting edge cost. The tool life for minimum cost given that cost of $$1$$ cutting edge is Rs.$$5$$, operator wages including the machine tool cost is Rs. $$75$$/hour and tool life equation is $$V{T^{0.1}}$$ is $$100.$$

In an orthogonal machining experiment using a tool having $${6^ \circ }.$$ Rake angle, the following data were collected. Cutting speed $$0.5$$ $$m/sec,$$ width of cut $$3$$ $$mm,$$ depth of cut $$1mn,$$ chip thickness $$1.5mm.$$ Assuming that shearing takes place under minimum energy condition,

Chip velocity is

In an orthogonal machining experiment using a tool having $${6^ \circ }.$$ Rake angle, the following data were collected. Cutting speed $$0.5$$ $$m/sec,$$ width of cut $$3$$ $$mm,$$ depth of cut $$1mn,$$ chip thickness $$1.5mm.$$ Assuming that shearing takes place under minimum energy condition,

Area of shear plane is

A part can be machined in $$30$$ minutes on an engine lathe where as it can be machined in $$6$$ minutes on a turret lathe. However, it would cost additionally Rs. $$500$$ to tool up the turret lathe for the operation. If the hourly rate including labour and overhead is Rs. $$80$$ for the engine lathe and Rs. $$160$$ for the turret lathe, The minimum number of parts required to make the turret lathe more economical to use, for the operation

Parting-off operation is carried out on a cylindrical work-piece of $$100mm$$ diameter. The groove width is $$2$$ $$mm$$ and an in feed of $$0.2$$ $$mm$$ per revolution is given at a maximum cutting speed of $$60$$ $$m/mm.$$ The specific cutting force for the material is $$800\,\,N/m{m^2}.$$

The tangential force on the tool is

Parting-off operation is carried out on a cylindrical work-piece of $$100mm$$ diameter. The groove width is $$2$$ $$mm$$ and an in feed of $$0.2$$ $$mm$$ per revolution is given at a maximum cutting speed of $$60$$ $$m/mm.$$ The specific cutting force for the material is $$800\,\,N/m{m^2}.$$

The maximum power requirement for the operation is

In an orthogonal cutting operation,
The depth of cut $$=2$$ $$mm,$$
Width of cut $$=15$$ $$mm,$$
Cutting speed $$=0.5$$ $$m/s$$ and
The rake angle $$=0$$ deg.
The cutting force and the thrust force are respectively $$900$$ $$N$$ and $$600$$ $$N$$ and the shear angle $$=30$$ $$deg$$.

The cutting power in watts is

In an orthogonal cutting operation,
The depth of cut $$=2$$ $$mm,$$
Width of cut $$=15$$ $$mm,$$
Cutting speed $$=0.5$$ $$m/s$$ and
The rake angle $$=0$$ deg.
The cutting force and the thrust force are respectively $$900$$ $$N$$ and $$600$$ $$N$$ and the shear angle $$=30$$ $$deg$$.

The average coefficient of friction between the chip and the tool is

In an orthogonal cutting operation, the cutting velocity is $$30$$ $$m/min$$ and the chip velocity $$15$$ $$m/min.$$ If the rake angle of the tool is $${10^0}$$.

The shear angle is

In an orthogonal cutting operation, the cutting velocity is $$30$$ $$m/min$$ and the chip velocity $$15$$ $$m/min.$$ If the rake angle of the tool is $${10^0}$$.

Shear velocity with the help of a velocity triangle.

In an orthogonal cutting operation,
The depth of cut $$=2$$ $$mm,$$
Width of cut $$=15$$ $$mm,$$
Cutting speed $$=0.5$$ $$m/s$$ and
The rake angle $$=0$$ deg.
The cutting force and the thrust force are respectively $$900$$ $$N$$ and $$600$$ $$N$$ and the shear angle $$=30$$ $$deg$$.

The length of the shear plane is

A generalized tool life equation for carbide tool for machining steel is given by
$$\,\,\,\,\,\,\,\,\,\,$$$$\,\,\,\,$$ $$V{T^a}{F^b}{D^c} = K,$$
Where $$V=$$ Cutting speed, meters/min,
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$T=$$ Tool life,
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$F=$$ feed, $$mm/rev,$$
$$D=$$ depth of cut in $$mm,$$ Indicates have magnitude $$a=0.3, b=0.3, c=0.15,$$

The change in productivity for the new processing conditions

A generalized tool life equation for carbide tool for machining steel is given by
$$\,\,\,\,\,\,\,\,\,\,$$$$\,\,\,\,$$ $$V{T^a}{F^b}{D^c} = K,$$
Where $$V=$$ Cutting speed, meters/min,
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$T=$$ Tool life,
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$F=$$ feed, $$mm/rev,$$
$$D=$$ depth of cut in $$mm,$$ Indicates have magnitude $$a=0.3, b=0.3, c=0.15,$$

If the feed is halved and depth of cut doubled, for identical tool life of $$60$$ minutes, the percentage change in speed

During orthogonal turning a steel rod at feed $$0.25$$ $$mm$$ per revolution and depth of cut $$4.00$$ $$mm$$ by a tool of geometry $${0^0},\, - {10^0},\,\,{8^0},\,\,{7^0},\,\,{15^0},\,\,{60^0},\,\,0\,\,(mm)\,\,;$$ the following observation were made: Tangential force $$=1,600N,$$ Axial force in feed direction $$=800$$ $$N,$$ Chip thickness $$=0.60$$ $$mm.$$ Find the coefficient of friction between chip tool interface and shear strength of work material from shear force.

The following data apply to machining a part on turret lathe and a general purpose lathe

The setup cost and the cost for special tooling on the turret lathe would be $$Rs.3000/-.$$ These costs are negligible on the general purpose lathe. Calculate the batch seize which justifies the use of turret lathe.

A parting tool has a ground front clearance angle of $${6^0}$$ and the back rake angle of $${10^0}$$. The tool, by mistake, was set $$1.5$$ $$mm$$ above the line of centers while machining a job of $$50$$ $$mm$$ out-side diameter.

The diameter of the job at which, while parting, the tool will start rubbing

A parting tool has a ground front clearance angle of $${6^0}$$ and the back rake angle of $${10^0}$$. The tool, by mistake, was set $$1.5$$ $$mm$$ above the line of centers while machining a job of $$50$$ $$mm$$ out-side diameter.

The effective rake and clearance angle are

Calculate the tonnage capacity of the broaching machine required to broach on the hole under the following conditions.
Diameter of the finished hole $$=75mm,$$
rise per tooth $$=0.03mm$$
Tooth pitch $$=10mm,$$
Length of the broach $$=750mm$$
Cutting speed $$=6m/min,$$
specific cutting pressure $$ = 1300 \times {t^{0.4}}\,\,N/m{m^2},$$ (Where $$t$$ is the uncut chip thickness)
If the tool and work handling time is $$0.5min,$$ estimate the production rate per hour

The results of machining steel with $$2$$ grades of tool material are given below. For a $$180$$ $$min.$$ Tool life which tool is recommended and why?

If the tool regrinding and changing time is $$15min,$$ the cutting speed for tool $$A$$ $$ahs$$ to be chosen ($$40m/min$$ or $$50m/min$$)