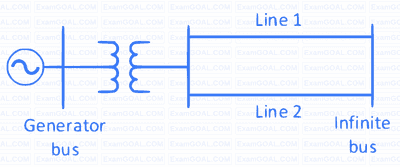
The single line diagram of a lossless system is shown in the figure. The system is operating in steady-state at a stable equilibrium point with the power output of the generator being $P_{max} \sin \delta$, where $\delta$ is the load angle and the mechanical power input is $0.5 P_{max}$. A fault occurs on line 2 such that the power output of the generator is less than $0.5 P_{max}$ during the fault. After the fault is cleared by opening line 2, the power output of the generator is $\left\{\frac{P_{max}}{\sqrt{2}} \right\} \sin \delta$. If the critical fault clearing angle is $\frac{\pi}{2}$ radians, the accelerating area on the power angle curve is ______ times $P_{max}$ (rounded off to 2 decimal places).

Suppose signal $y(t)$ is obtained by the time-reversal of signal $x(t)$, i.e., $y(t) = x(-t)$, $-\infty < t < \infty$. Which one of the following options is always true for the convolution of $x(t)$ and $y(t)$?

If $u(t)$ is the unit step function, then the region of convergence (ROC) of the Laplace transform of the signal $x(t) = e^{t^2}[u(t-1)-u(t-10)]$ is

Let $X(\omega)$ be the Fourier transform of the signal

$x(t) = e^{-t^4} \cos t, \quad -\infty < t < \infty$.

The value of the derivative of $X(\omega)$ at $\, \omega = 0$ is ______ (rounded off to 1 decimal place).