Consider the cascaded system as shown in the figure. Neglecting the faster component of the transient response, which one of the following options is a first-order pole-only approximation such that the steady-state values of the unit step responses of the original and the approximated systems are same?

Consider the closed-loop system shown in the figure with $$G(s) = \frac{K(s^2 - 2s + 2)}{(s^2 + 2s + 5)}.$$ The root locus for the closed-loop system is to be drawn for $0 \leq K < \infty$. The angle of departure (between $0^{o}$ and $360^{o})$ of the root locus branch drawn from the pole $(−1 + j2)$, in degrees, is _________________ (rounded off to the nearest integer).
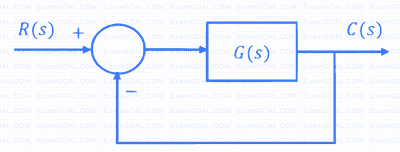
Consider the stable closed-loop system shown in the figure. The asymptotic Bode magnitude plot of $G(s)$ has a constant slope of $-20$ dB/decade at least till $100$ rad/sec with the gain crossover frequency being $10$ rad/sec. The asymptotic Bode phase plot remains constant at $-90^{o}$ at least till $\omega = 10$ rad/sec. The steady-state error of the closed-loop system for a unit ramp input is ________________ (rounded off to 2 decimal places).

Consider the stable closed-loop system shown in the figure. The magnitude and phase values of the frequency response of $G(s)$ are given in the table. The value of the gain $K_I$ ($>0$) for a $50^\circ$ phase margin is _____ (rounded off to 2 decimal places).
| $\omega$ in rad/sec | Magnitude in dB | Phase in degrees |
|---|---|---|
| 0.5 | −7 | −40 |
| 1.0 | −10 | −80 |
| 2.0 | −18 | −130 |
| 10.0 | −40 | −200 |
