Consider the standard second-order system of the form $\frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}$ with the poles $p$ and $p^\ast$ having negative real parts. The pole locations are also shown in the figure. Now consider two such second-order systems as defined below:

System 1: $\omega_n = 3$ rad/sec and $\theta = 60^{\circ}$
System 2: $\omega_n = 1$ rad/sec and $\theta = 70^{\circ}$

Which one of the following statements is correct?

Consider the cascaded system as shown in the figure. Neglecting the faster component of the transient response, which one of the following options is a first-order pole-only approximation such that the steady-state values of the unit step responses of the original and the approximated systems are same?

Consider the closed-loop system shown in the figure with $$G(s) = \frac{K(s^2 - 2s + 2)}{(s^2 + 2s + 5)}.$$ The root locus for the closed-loop system is to be drawn for $0 \leq K < \infty$. The angle of departure (between $0^{o}$ and $360^{o})$ of the root locus branch drawn from the pole $(−1 + j2)$, in degrees, is _________________ (rounded off to the nearest integer).

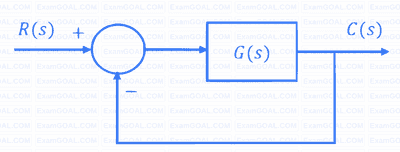
Consider the stable closed-loop system shown in the figure. The asymptotic Bode magnitude plot of $G(s)$ has a constant slope of $-20$ dB/decade at least till $100$ rad/sec with the gain crossover frequency being $10$ rad/sec. The asymptotic Bode phase plot remains constant at $-90^{o}$ at least till $\omega = 10$ rad/sec. The steady-state error of the closed-loop system for a unit ramp input is ________________ (rounded off to 2 decimal places).