For the three-bus lossless power network shown in the figure, the voltage magnitudes at all the buses are equal to 1 per unit (pu), and the differences of the voltage phase angles are very small. The line reactances are marked in the figure, where $\alpha$, $\beta$, $\gamma$, and $x$ are strictly positive. The bus injections $P_1$ and $P_2$ are in pu. If $P_1 = mP_2$, where $m > 0$, and the real power flow from bus 1 to bus 2 is 0 pu, then which one of the following options is correct?

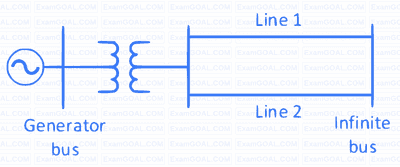
The single line diagram of a lossless system is shown in the figure. The system is operating in steady-state at a stable equilibrium point with the power output of the generator being $P_{max} \sin \delta$, where $\delta$ is the load angle and the mechanical power input is $0.5 P_{max}$. A fault occurs on line 2 such that the power output of the generator is less than $0.5 P_{max}$ during the fault. After the fault is cleared by opening line 2, the power output of the generator is $\left\{\frac{P_{max}}{\sqrt{2}} \right\} \sin \delta$. If the critical fault clearing angle is $\frac{\pi}{2}$ radians, the accelerating area on the power angle curve is ______ times $P_{max}$ (rounded off to 2 decimal places).

Suppose signal $y(t)$ is obtained by the time-reversal of signal $x(t)$, i.e., $y(t) = x(-t)$, $-\infty < t < \infty$. Which one of the following options is always true for the convolution of $x(t)$ and $y(t)$?

If $u(t)$ is the unit step function, then the region of convergence (ROC) of the Laplace transform of the signal $x(t) = e^{t^2}[u(t-1)-u(t-10)]$ is