Assuming all numbers are in $$2's$$ complement representation, which of the following numbers is divisible by $$11111011?$$

The literal count of a Boolean expression is the sum of the number of times each literal appears in the expression. For example, the literal count of $$(xy + xz)$$ is $$4.$$ What are the minimum possible literal counts of the product -of -sum and sum -of-product representations respectively of the function given by the following Karnaugh map? Here, $$X$$ denotes “don’t care”

A 1- input, 2- output synchronous sequential circuit behaves as follows.

Let $${z_k},\,{n_k}$$ denote the number of $$0’s$$ and $$1’s$$ respectively in initial $$k$$ bits of the input

$$\left({{z_k} + {n_k} = k} \right).$$ The circuit outputs $$00$$ until one of the following conditions holds.

$$ * \,\,\,\,\,$$ $${z_k} = {n_k} + 2.\,\,\,$$ In this case, the output at the $$k$$-th and all subsequent clock ticks is $$10.$$

$$ * \,\,\,\,\,$$ $${n_k} = {z_k} + 2.\,\,\,$$ In this case, the output at the $$k$$-th and all subsequent clock ticks is $$01.$$

What is the minimum number of states required in the state transition graph of the above circuit?

Consider the following circuit composed of $$XOR$$ gates are non-inverting buffers.

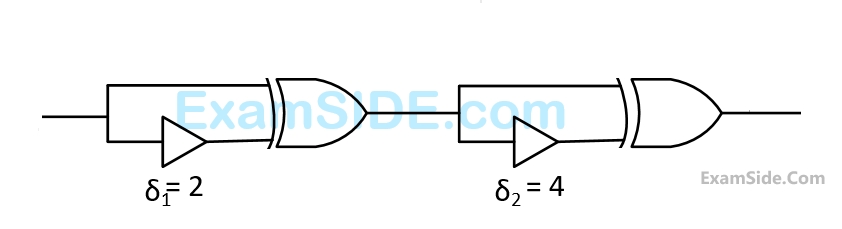
The non-inverting buffers have delays $${\delta _1} = 2$$ $$ns$$ and $${\delta _2} = 4$$ $$ns$$ as shown in the figure. Both $$XOR$$ gates and all wires have zero delay. Assume that all gate inputs, outputs and wires are stable at logic level $$0$$ at time$$0.$$ If the following waveform is applied at input $$A$$, how many transition(s) (change of logic levels) occurs(s) at $$B$$ during the interval from $$0$$ to $$10$$ $$ns?$$