WB JEE 2022 | Heat and Thermodynamics Question 12 | Physics

WB JEE 2022

MCQ (Single Correct Answer)

-0.25

One mole of a diatomic ideal gas undergoes a process shown in P-V diagram. The total heat given to the gas (ln 2 = 0.7) is

WB JEE 2022 Physics - Heat and Thermodynamics Question 11 English

2.5 P₀V₀

3.9 P₀V₀

1.1 P₀V₀

1.4 P₀V₀

WB JEE 2022

MCQ (Single Correct Answer)

-0.5

One mole of an ideal monoatomic gas expands along the polytrope PV³ = constant from V₁ to V₂ at a constant pressure P₁. The temperature during the process is such that molar specific heat $${C_V} = {{3R} \over 2}$$. The total heat absorbed during the process can be expressed as

$${P_1}{V_1}\left( {{{V_1^2} \over {V_2^2}} + 1} \right)$$

$${P_1}{V_1}\left( {{{V_1^2} \over {V_2^2}} - 1} \right)$$

$${P_1}{V_1}\left( {{{V_1^3} \over {V_2^2}} - 1} \right)$$

$${P_1}{V_1}\left( {{{V_1^{}} \over {V_2^2}} - 1} \right)$$

WB JEE 2021

MCQ (Single Correct Answer)

-0.25

WB JEE 2021 Physics - Heat and Thermodynamics Question 15 English

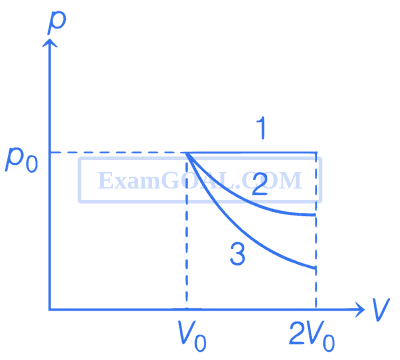
In the given figure, 1 represents isobaric, 2 represents isothermal and 3 represents adiabatic processes of an ideal gas. If $$\Delta$$U₁, $$\Delta$$U₂ and $$\Delta$$U₃ be the changes in internal energy in these processes respectively, then

$$\Delta$$U₁ < $$\Delta$$U₂ < $$\Delta$$U₃

$$\Delta$$U₁ > $$\Delta$$U₂ < $$\Delta$$U₃

$$\Delta$$U₁ = $$\Delta$$U₂ > $$\Delta$$U₃

$$\Delta$$U₁ > $$\Delta$$U₂ > $$\Delta$$U₃

WB JEE 2021

MCQ (Single Correct Answer)

-0.25

If pressure of real gas O₂, in a container is given by $$p = {{RT} \over {2V - b}} - {a \over {4{b^2}}}$$, then the mass of the gas in the container is

32 g

16 g

4 g

64 g

PREVIOUS NEXT

WB JEE Subjects