Identify the conjugate acid-base pair respectively from following equilibrium reaction.

$$ \mathrm{HPO}_{4(\mathrm{aq})}^{2-}+\mathrm{H}_2 \mathrm{O}_{(\ell)} \rightleftharpoons \mathrm{PO}_{4(\mathrm{aq})}^{3-}+\mathrm{H}_3 \mathrm{O}_{(\mathrm{eq})}^{+} $$

Which from following nitrogen bases either of purine or pyrimidine does NOT contain $-\mathrm{NH}_2$ group attached with its ring?

Which from following amino acids contains heterocyclic ring at a side chain (R) group?

Calculate the volume occupied by all particles in fcc unit cell if volume of unit cell is $1.6 \times 10^{-23} \mathrm{~cm}^3$.

Calculate the number of $\mathrm{Cl}^{-}$ions in 222 g unhydrous calcium chloride?

(At. mass $\mathrm{Ca}=40, \mathrm{Cl}=35.5$ )

Which from following mixtures exhibits positive deviation from Raoult's law?

What is the difference in oxidation number of Mn in $\mathrm{KMnO}_4$ and $\mathrm{MnO}_2$ ?

Calculate the work done in joule if 2 moles of an ideal gas expand isothermally from $15.5 \mathrm{dm}^3$ to $20 \mathrm{dm}^3$ at constant pressure 1 atm .

Nitric oxide reacts with $\mathrm{H}_2$ according to reaction. $2 \mathrm{NO}_{(\mathrm{g})}+2 \mathrm{H}_{2(\mathrm{~g})} \rightarrow \mathrm{N}_{2(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{g})}$, identify correct relation for disappearance of reactant and appearance of product.

The solubility of sparingly soluble salt $\mathrm{AX}_2$ is $1 \times 10^{-4} \mathrm{~mol} \mathrm{dm}^{-3}$ at 298 K . Calculate its solubility product.

Which of the following is used as Green solvent?

What is vapour density of $\mathrm{O}_2$ gas?

Identify the correct statement regarding geometry and lone pair of electrons present in $\mathrm{CH}_4$ and $\mathrm{SiCl}_4$.

What type of hybridisation is present in square planar geometry of complex $\left[\mathrm{Ni}(\mathrm{CN})_4\right]^{2-}$

What are the different types of bonds formed by sulphur with oxygen in thiosulfuric acid?

Which of the following is not an alkali metal?

What is formula of mustard gas?

Rate law for the reaction $\mathrm{aA}+\mathrm{bB} \rightarrow \mathrm{cC}+\mathrm{dD}$ is $r=k[A][B]$, the rate of reaction doubles if

Which of the following reactions exhibit minimum standard reduction potential?

Which from following dopants is used in germanium to produce p-type semiconductor?

Calculate the osmotic pressure of 0.5 M aqueous solution of nonvolatile solute at 300 K .

$$ \left[\mathrm{R}=0.0821 \mathrm{~atm} \mathrm{dm} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right] $$

1.8 g water is vapourised by supplying 4 kJ heat at $100^{\circ} \mathrm{C}$. What is the heat of vapourisation of water at same temperature?

Calculate the number of moles of nonvolatile solute dissolved in 0.3 kg solvent if $\Delta \mathrm{T}_{\mathrm{b}}=0.3 \mathrm{~K}$ and $\mathrm{K}_{\mathrm{b}}$ for solvent is $1.8 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$.

Which from following is NOT hydrogen like species?

Identify the monomer of natural rubber.

Identify strongest base from following in aqueous medium.

Identify neutral ligand from following.

Identify a weakest base from following

Which among the following has lowest boiling point?

Which from following is a non benzenoid aromatic compound?

Phenol on reaction with aqueous solution of bromine gives

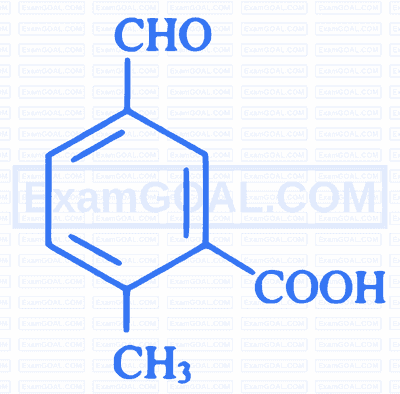
What is IUPAC name of the following compound?

Which of the following is a bond line structure of glycerol?

Which of the following has highest reactivity for $\mathrm{S}_{\mathrm{N}} 1$ reactions?

The reaction of bromobenzene with bromomethane and sodium metal in dry ether to give toluene is

What is the number of structural isomers possible for alkene with molecular formula $\mathrm{C}_5 \mathrm{H}_{10}$ ?

If standard reduction potential $\left(E^{\circ}\right)$ of $\left(\mathrm{Ni}_{(\mathrm{aq})}^{+2} \mid \mathrm{Ni}_{(\mathrm{s})}\right)$ and $\left(\mathrm{Al}_{(\mathrm{aq})}^{+3} \mid \mathrm{Al}_{(\mathrm{s})}\right)$ are -0.25 V and -1.66 V respectively. What is standard emf of cell reaction $2 \mathrm{Al}_{(\mathrm{s})}+3 \mathrm{Ni}_{(\mathrm{aq})}^{+2} \longrightarrow 2 \mathrm{Al}_{(\mathrm{aq})}^{+3}+3 \mathrm{Ni}_{(\mathrm{s})}$

Which of the following is NOT obtained when a mixture of chloroethane and 1-chloropropane is treated with sodium metal in dry ether?

Calculate the value of dissociation constant of weak monoacidic base if it dissociates to $2 \%$ in 0.1 M solution?

Which from following process does NOT results in coagulation?

Calculate the number of unit cell in $1 \mathrm{~cm}^3$ volume of metal if volume of unit cell is $3.448 \times 10^{-23} \mathrm{~cm}^3$

Identify the catalyst used in following reaction at $500^{\circ} \mathrm{C}$ ?

$$ \mathrm{CO}+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{CO}_2+\mathrm{H}_2 $$

Hydroboration-oxidation of but-1-ene forms

Which from following reactión results in azo coupling?

Identify the source of gallic acid from following

Calculate the standard enthalpy change of following reaction

$$ \begin{aligned} & \mathrm{CH}_{4(\mathrm{~g})}+2 \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{CO}_{2(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\ell)} \\ & \text { If } \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{CH}_4\right)=-75 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{CO}_2\right)=-394 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{H}_2 \mathrm{O}\right)=-286 \mathrm{~kJ} \mathrm{~mol}^{-1} \end{aligned} $$

Identify the product ' B ' in following reaction.

Dry ice $\xrightarrow[\text { dry ether }]{\mathrm{CH}_3 \mathrm{MgBr}} \mathrm{A} \xrightarrow{\mathrm{H}_3 \mathrm{O}^{+}} \mathrm{B}$

Which from following polymers is used to prepare shoe soles?

Half life of a first order reaction is 20 minutes. The time taken to reduce the initial concentration of reactant to $(1 / 10)^{\text {th }}$ is _________

If $\mathrm{E}^{\cdot}\left(\mathrm{Mg}_{(\mathrm{aq})}^{+2} \mid \mathrm{Mg}_{(\mathrm{s})}\right)=-2.37 \mathrm{~V}$. What is potential for $\mathrm{Mg}_{(\mathrm{s})} \longrightarrow \mathrm{Mg}^{+2}(0.01 \mathrm{M})+2 \mathrm{e}^{-}$at 298 K ?

If $y=y(x)$ and $\left(\frac{2+\sin x}{y+1}\right) \frac{\mathrm{d} y}{\mathrm{~d} x}=-\cos x, y(0)=1$, then $y\left(\frac{\pi}{2}\right)=$

If $A=\left[\begin{array}{cc}1 & \cot \frac{\theta}{2} \\ -\cot \frac{\theta}{2} & 1\end{array}\right]$ then $A^{-1}=$

If $\bar{a}, \bar{b}, \bar{c}$ are three unit vectors such that $|\overline{\mathrm{a}}+\overline{\mathrm{b}}|^2+|\overline{\mathrm{a}}+\overline{\mathrm{c}}|^2=8$, then $|\overline{\mathrm{a}}+3 \overline{\mathrm{~b}}|^2+|\overline{\mathrm{a}}+3 \overline{\mathrm{c}}|^2=$

The probability that a certain kind of component will survive a given test is $\frac{2}{3}$. The probability that at most 2 components out of 4 tested, will survive is

From the following options, the nearest line to the origin is ….

If the truth value of the statement pattern $[p \wedge \sim r] \rightarrow \sim r \wedge q$ is False, then which of the following has truth value False?

$\bar{a}=\hat{i}-\hat{j}, \bar{b}=\hat{j}-\hat{k}, \bar{c}=\hat{k}-\hat{i}$ then a unit vector $\bar{d}$ such that $\overline{\mathrm{a}} \cdot \overline{\mathrm{d}}=0=[\overline{\mathrm{b}} \overline{\mathrm{c}} \overline{\mathrm{d}}]$ is

In $\triangle A B C$, with usual notations, if $\mathrm{a}^4+\mathrm{b}^4+\mathrm{c}^4-2 \mathrm{a}^2 \mathrm{c}^2-2 \mathrm{c}^2 \mathrm{~b}^2=0$, then $\angle \mathrm{C}=\ldots$

If the planes $\overline{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}-\lambda \hat{\mathrm{j}}+\hat{\mathrm{k}})=3$ and $\overline{\mathrm{r}} \cdot(4 \hat{\mathrm{i}}-\hat{\mathrm{j}}+\mu \hat{\mathrm{k}})=5$ are parallel, then $\lambda+\mu=$

If $x$ is real, then the difference between the greatest and least values of $\frac{x^2-x+1}{x^2+x+1}$ is

The perimeter of a square whose two sides have equations $\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{4}$ and $\frac{x}{2}=\frac{y-1}{3}=\frac{z+1}{4}$ is

In a triangle ABC with usual notations if, $\tan \left(\frac{\mathrm{B}-\mathrm{C}}{2}\right)=x \cot \frac{\mathrm{~A}}{2}$, then $x=$

A coin is tossed until one head appears or a tail appears 4 times in succession. The probability distribution of the number of tosses is

The degree of the differential equation $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}+3\left(\frac{\mathrm{~d} y}{\mathrm{~d} x}\right)^2=x^2 \log \left(\frac{\mathrm{~d}^2 y}{\mathrm{~d} x^2}\right)$ is

If the sum of the squares of the distances of a point $\mathrm{P}(x, y, z)$ from the three co-ordinate axes is 324 , then the distance of point P from the origin is ….

For a real number $x,[x]$ denotes the greatest integer less than or equal to $x$. Then the value of

$$ \begin{array}{r} {\left[\frac{1}{2}\right]+\left[\frac{1}{2}+\frac{1}{100}\right]+\left[\frac{1}{2}+\frac{2}{100}\right]+\left[\frac{1}{2}+\frac{3}{100}\right]+} \left[\frac{1}{2}+\frac{99}{100}\right]= \end{array} $$

The angle between the lines $3 x=2 y=-\mathrm{z}$ and $-x=6 y=-4 z$ is

If $y+\frac{\mathrm{d}}{\mathrm{d} x}(x y)=x(\sin x+\log x)$ then

If the pair of straight lines $x y-x+y-1=0$ and the line $x+\mathrm{k} y-3=0$ are concurrent, then the value of $k$ is equal to

If the function

$$ f(x)=\left\{\begin{array}{cc} x+a \sqrt{2} \sin x & \text { if } 0 \leq x \leq \frac{\pi}{4} \\ 2 x \cot x+b & \text { if } \frac{\pi}{4} < x \leq \frac{\pi}{2} \\ a \cos 2 x-b \sin x & \text { if } \frac{\pi}{2} < x \leq \pi \end{array}\right. $$

is continuous in $[0, \pi]$ then $a-b=$

Which of the following statements has the truth value T ?

A: cube roots of unity are in Geometric progression and their sum is 1

B: $4+7>10$ iff $2+8<10$

C: $\exists x \in \mathbb{N}$ such that $x^2-3 x+2=0$ and $\exists \mathrm{n} \in \mathbb{N}$ such that n is an odd number

D: $3+\mathrm{i}$ is a complex number or $\sqrt{2}+\sqrt{3}=\sqrt{5}$

The p.d.f. of a continuous random variable X is $f(x)=\left\{\begin{array}{cl}\frac{x^2}{18} & , \text { if }-3 < x < 3 \\ 0 & \text { otherwise }\end{array}\right.$

Then $\mathrm{P}[|\mathrm{X}|<2]=$

The population of a town increases at a rate proportional to the population at that time. If the population increases from forty thousand to eighty thousand in 20 years, then the population in another 40 years will be

If the vectors $m \hat{i}+m \hat{j}+n \hat{k}, \hat{i}+\hat{k}, n \hat{i}+n \hat{j}+p \hat{k}$ lie in a plane then…

The value of

$$ \begin{aligned} \sin ^2 5^{\circ}+\sin ^2 10^{\circ} & +\sin ^2 15 +\ldots \ldots \ldots \ldots \ldots \ldots+\sin ^2 85^{\circ}+\sin ^2 90^{\circ}= \end{aligned} $$

The area bounded by the curve $x=2-y-y^2$ and the Y -axis is

If $y=\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)+\sec ^{-1}\left(\frac{1+x^2}{1-x^2}\right)$ then the value of $\frac{d y}{d x}$ at $x=\sqrt{3}$ is

$$ \int_{\frac{\pi}{3}}^{\frac{2 \pi}{3}} \frac{x}{1+\sin x} d x= $$

$$ \int_0^2 \frac{3 x+1}{x^2+4} d x= $$

$$ \int \frac{\sin 2 x \cos 2 x}{\sqrt{9-\cos ^4 2 x}} d x= $$

$$ \int \frac{\cos 2 x-\cos 2 \alpha}{\cos x-\cos \alpha} d x= $$

21 friends were invited for a party. Two round tables can accommodate 12 and 9 friends each, The number of ways of the seating arrangements of friends is …..

The area of a parallelogram whose diagonals are the vectors $2 \bar{a}-\bar{b}$ and $4 \bar{a}-5 \bar{b}$, where $\bar{a}$ and $\bar{b}$ are unit vectors forming an angle of $45^{\circ}$ is

$$ \lim\limits_{x \rightarrow \infty}\left(\frac{x+8}{x+1}\right)^{x+5}=\ldots $$

$$ \cot ^{-1}\left(2 \cos \left(2 \operatorname{cosec}^{-1}(\sqrt{2})\right)\right)=\ldots $$

If $\mathrm{z}=x+\mathrm{i} y$ is a complex number, then the equation $\left|\frac{z+i}{z-i}\right|=\sqrt{3}$ represents the

If $\int \frac{2 x^2+3}{\left(x^2-1\right)\left(x^2-4\right)} \mathrm{d} x=\log \left[\left(\frac{x-2}{x+2}\right)^{\mathrm{a}} \cdot\left(\frac{x+1}{x-1}\right)^{\mathrm{b}}\right]+\mathrm{c}$, (where c is the constant of integration) then the value of $a+b$ is equal to

For $N \in \mathbb{N}, \frac{\mathrm{~d}^{\mathrm{n}}}{\mathrm{d} x^{\mathrm{n}}}(\log x)=$

In a single toss of a fair die, the odds against the event that number 4 or 5 turns up is

If $\mathrm{f}(x)=x \cdot \mathrm{e}^{x(1-x)}$, then $\mathrm{f}(x)$ is

The approximate value of $\sqrt[3]{64 \cdot 04}$ is

The X and Y intercepts of the tangent to the hyperbola $\frac{x^2}{20}-\frac{y^2}{5}=1$ which is perpendicular to the line $4 x+3 y=7$, are respectively

If the lines $\frac{x-1}{2}=\frac{y+1}{\mathrm{k}}=\frac{\mathrm{z}}{2}$ and $\frac{x+1}{5}=\frac{y+1}{2}=\frac{\mathrm{z}}{\mathrm{k}}$ are coplanar, then the equation of the plane containing these lines are

The line $y=\mathrm{m} x+3$ is tangent to the parabola $y^2=4 x$, if the value of m is

If the tangent and the normal at the point $(\sqrt{3}, 1)$ to the circle $x^2+y^{2 }=4$, and the X -axis form a triangle, then the area (in sq.units) of this triangle is

If $3 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right)-4 \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)+2 \tan ^{-1}\left(\frac{2 x}{1-x^2}\right)=\frac{\pi}{3}$ then the value of $x=$

If $x=\operatorname{acos}^3 \theta y=\operatorname{asin}^3 \theta$

Then $\sqrt{1+\left(\frac{\mathrm{d} y}{\mathrm{~d} x}\right)^2}=$

If the difference between the maximum and minimum values of the objective function $\mathrm{z}=7 x-8 y$, subject to the constraints $x+y \leqslant 20, y \geqslant 5, x, y \geqslant 0$ is $5 \mathrm{k}+200$, then the value of k is

The number of solutions of $16^{\sin ^2 x}+16^{\cos ^2 x}=10$ in $0 \leqslant x \leqslant 2 \pi$ are

Let the line $\frac{x-2}{3}=\frac{y-1}{-5}=\frac{z+2}{2}$ lie in the plane $x+3 y-\alpha z+\beta=0$, then the value of $(\beta-\alpha)$ is equal to

A vehicle is moving with uniform speed along 3 different shaped roads as horizontal, concave and convex. The surface of road on which, the normal reaction on vehicle is maximum is

${ }_{88} \mathrm{R}_{\mathrm{a}}^{226}$ is converted into ${ }_{82} \mathrm{P}_{\mathrm{b}}^{206}$ by emission of alpha ( $\alpha$ ) and beta ( $\beta$ ) particles. The number of alpha and beta particles emitted are respectively

In a Young's double slit experiment wavelength of light used is $6000 \mathop {\rm{A}}\limits^{\rm{o}}$. The first order maxima and tenth order maxima fall at 14.50 mm and 16.75 mm from the particular reference point in the interference pattern respectively. If the wavelength is changed to $5500 \mathop {\rm{A}}\limits^{\rm{o}}$ then the position of zero order and tenth order maxima are respectively

[The other arrangements remaining same]

In a pure silicon crystal electron-hole concentration is $10^{16}$ per $\mathrm{m}^3$ at 301 K . Now $10^{21}$ atoms of phosphorus are added per cubic metre. The new hole concentration in silicon is (in per $\mathrm{m}^3$ )

Assuming human pupil to have radius of 0.25 cm and comfortable viewing distance of 25 cm , the minimum separation between the two objects that human eye can resolve at 500 nm wavelength is nearly

Four charges $2 \mu \mathrm{C},-3 \mu \mathrm{C}, 4 \mu \mathrm{C},-4 \mu \mathrm{C}$ and $-1 \mu \mathrm{C}$ are enclosed by the Gaussian surface of radius 2 m . Net outward flux through the Gaussian surface is (in $\mu \mathrm{V}-\mathrm{m}$ ) [ $\varepsilon_0=$ permittivity of free space]

A solid sphere of mass ' $m$ ' and radius ' $R$ ' is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with angular speed twice that of sphere. The ratio of kinetic energy of sphere to kinetic energy of cylinder will be

A person standing between two parallel cliffs fires a gun and hears two echoes, first echo after 1 second and the second echo after 3 second. The distance between the two cliffs is (Velocity of sound $=340 \mathrm{~m} / \mathrm{s}$ )

A series combination of 10 capacitors, each of value ' $\mathrm{C}_1$ ' is charged by a source of potential difference ' 4 V '. When another parallel combination of 8 capacitors, each of value ' $\mathrm{C}_2$ ' is charged by a source of potential difference ' V ', it has the same total energy stored in it as in the first combination. The value of ' $\mathrm{C}_2$ ' is

A solid sphere and thin walled hollow sphere have same mass and same material. Which of them have greater moment of inertia about their diameter?

[ $\mathrm{I}_{\mathrm{h}}=$ moment of inertia of hollow sphere about an axis coinciding with its diameter, $\mathrm{I}_5=$ moment of inertia of solid sphere about an axis coinciding with its diameter]

The total charge induced in a conducting loop when it is moved in a uniform magnetic field depends on

A rectangular film of liquid is expanded from $(5 \mathrm{~cm} \times 4 \mathrm{~cm})$ to $(7 \mathrm{~cm} \times 8 \mathrm{~cm})$. If the work done is $3 \times 10^{-4} \mathrm{~J}$, the surface tension of the liquid is (nearly)

The temperature of a body on Kelvin scale is ' $x$ ' $K$. When it is measured by a Fahrenheit thermometer, it is found to be ' x ' ${ }^{\circ} \mathrm{F}$. The value of ' $x$ ' is (nearly)

A capillary tube is taken from earth's surface to moon's surface. The rise of liquid column on the moon's surface is (acceleration due to gravity on the earth's surface is six times that of moon's surface)

For a gas at a particular temperature on an average, the quantity which remains same for all molecules is

In a common emitter transistor amplifier, the output voltage and input voltage have a phase difference of

A body of mass 100 gram is tied to a spring of spring constant $8 \mathrm{~N} / \mathrm{m}$, while the other end of a spring is fixed. If the body moves in a circular path on smooth horizontal surface with constant angular speed $8 \mathrm{rad} / \mathrm{s}$ then the ratio of extension in the spring to its natured length will be

The voltmeter has range 10 V and its internal resistance is $50 \Omega$. To increase the range of voltmeter to 15 V , the resistance which is to be connected is

If 120 J of thermal energy is incident on area $3 \mathrm{~m}^2$, the amount of heat transmitted is 12 J , coefficient of absorption is 0.6 , then the amount of heat reflected is

A circular coil of wire consisting of ' $n$ ' tums each of radius 8 cm carries a current of 0.4 A . The magnitude of the magnetic field at the centre of coil is $3.14 \times 10^{-4} \mathrm{~T}$. The value of ' $n$ ' is

[Take $\mu_0=12.56 \times 10^{-7}$ SI unit]

The graph shows the variation of voltage (v) across the plates of two parallel plate capacitos $A$ and $B$ versus increase of charge $Q$ stored in them. Then

If force $\vec{F}=-3 \hat{i}+\hat{j}+5 \hat{k}$ acts along $\vec{r}=7 \hat{i}+3 \hat{j}+\hat{k}$ then the torque acting at that point is

Susceptibility of a paramagnetic substance is

When an ideal gas $\left(\gamma=\frac{5}{3}\right)$ is heated under constant pressure, then what percentage of given heat energy will be utilised in doing external work?

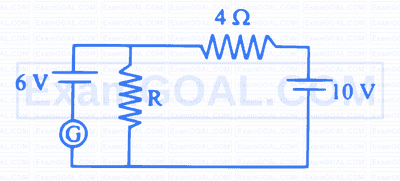
In the given electrical network, the value of resistance ' $R$ ' when the current in the galvanometer will be zero, is

When a photosensitive metal surface is illuminated with radiation of wavelength ' $\lambda_1$ ', the stopping potential is ' $\mathrm{V}_1$ '. If the same surface is illuminated with radiation of wavelength ' $3 \lambda_1$ ', the stopping potential is $\frac{\mathrm{V}_1}{6}$. The threshold wavelength for the photosensitive metal surface is

The mean kinetic energy of the molecules of an ideal gas at $399^{\circ} \mathrm{C}$ is ' E '. The temperature at which the mean kinetic energy of its molecules will be ' $\mathrm{E} / 2$ ', is

Three capacitors each of capacitance ' C ' and breakdown voltage ' $V$ ' are connected in series. The capacitance and breakdown voltage of the series combination will be respectively

When alternating current is passed through $\mathrm{L}-\mathrm{R}$ series circuit, the power factor is $\frac{\sqrt{3}}{2}$ and $\mathrm{R}=50 \Omega$, then the value of L is

$$ \left[\cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}, \sin \frac{\pi}{6}=\frac{1}{2}, \tan \frac{\pi}{6}=\frac{1}{\sqrt{3}}\right] $$

Time period of a simple pendulum on earth's surface is ' T '. It time period becomes ' xT ' when taken to a height ' $2 R$ ' above earth's surface. The value of $x$ will be $(R=$ radius of earth)

The wire loop PQRSP formed by joining two semicircular wire of radii $R_1$ and $R_2$ carries a current $I$ as shown. The magnitude of the magnetic field at the centre ' O ' is

A body of mass 1 kg begins to move under the action of a time dependent force $\overrightarrow{\mathrm{F}}=\left(\hat{\mathrm{t}}+2 t^2 \hat{\mathrm{j}}\right) \mathrm{N}$, where $\hat{i}$ and $\hat{j}$ are unit vectors along $x$ and $y$ axis. The power developed by above force at time $\mathrm{t}=3$ second will be

The period of oscillating simple pendulum is $\mathrm{T}=2 \pi \sqrt{\frac{l}{\mathrm{~g}}}$ where length ' $l$ ' is 100 cm with error 1 mm . Period is 2 second. The time of 100 oscillations is measured by a stopwatch of least count 0.1s. The percentage error in gravitational acceleration ' g ' is

If a centre tap transformer is used with two p-n junction diodes for full wave rectification then output voltage of rectifier with respect to each diode is (secondary voltage of transformer $=\mathrm{V}_{\mathrm{s}}$ )

Out of the following transitions in hydrogen atom, identify the transition which emits photons of highest frequency.

An organ pipe has fundamental frequency 80 Hz . If its one end is closed, the frequencies produced will be (in Hz ) (Neglect end correction)

An a.c. e.m.f. of peak value 230 V and frequency 50 Hz is connected to a circuit with $\mathrm{R}=11.5 \Omega, \mathrm{~L}=2.5 \mathrm{H}$ and a capacitor all in series. The value of capacitance is ' $C$ ' for the current in the circuit to be maximum. The value of ' $C$ ' and maximum current are respectively ( $\pi^2=10$ )

A gas undergoes a change in which its pressure ' P ' and volume ' V ' are related as $\mathrm{PV}^{\mathrm{n}}=$ constant, where n is a constant. If the specific heat of the gas in this change is zero, then the value of $n$ is ( $\gamma=$ adiabatic ratio)

From photoelectric effect experiment, select the correct statement.

The equation of wave is $y=60 \sin (1200 t-6 x)$, where ' $y$ ' is in micron, ' $t$ ' is in second and ' $x$ ' is in metre. The ratio of maximum particle velocity to the wave velocity of wave propagation is

Two satellites P and Q go round a planet in circular orbits having radii ' $3 R$ ' and ' $R$ ' respectively. If the speed of satellite $P$ is ' $2 V$ ', the speed of the satellite $Q$ will be

For a particle performing S.H.M.; the total energy is ' $n$ ' times the kinetic energy, when the displacement of a particle from mean position is $\frac{\sqrt{3}}{2} \mathrm{~A}$, where A is the amplitude of S.H.M. The value of ' $n$ ' is

A copper ring is held horizontally and a bar magnet is dropped through the ring with its length along the axis of the ring. The acceleration of the falling magnet while it is passing through the ring is

In a single slit diffraction pattern, identify the incorrect statement from the following.

If an alternating voltage is applied across a p-n junction diode in series with a load then

Two waves of same frequency ( n ) are approaching each other with same velocity $12 \mathrm{~m} / \mathrm{s}$ along the same linear path and interfere. The distance between two consecutive nodes is

A coil of resistance $400 \Omega$ is placed in ${ }^3$ magnetic field. If the magnetic flux ' $\phi$, ( Wb ) linked with the coil varies with time ' $t$ ' ( $s$ ) ${ }^{\text {is }} \phi=50 \mathrm{t}^2+4$, the current in the coil at $\mathrm{t}=2 \mathrm{~s}$ will be