What is IUPAC name of hydroquinone?

Which from following amino acids contains ' S ' in its side chain $(\mathrm{R})$ ?

Which from following elements forms coloured compound in its respective oxidation state?

What different types of bonds are formed by chlorine with oxygen in perchloric acid?

Calculate the volume of fcc unit cell in $\mathrm{cm}^3$ if void volume of it is $4.16 \times 10^{-24} \mathrm{~cm}^3$.

Calculate standard enthalpy change of reaction

$$ \mathrm{C}_2 \mathrm{H}_{2(\mathrm{~g})}+\frac{5}{2} \mathrm{O}_{2(\mathrm{~g})} \longrightarrow 2 \mathrm{CO}_{2(\mathrm{~g})}+\mathrm{H}_2 \mathrm{O}_{(\mathrm{l})}, \text { if } $$

$$ \begin{aligned} & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{CO}_2\right)=-393 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{H}_2 \mathrm{O}\right)=-286 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{C}_2 \mathrm{H}_2\right)=227 \mathrm{~kJ} \mathrm{~mol}^{-1} \end{aligned} $$

Which from following formulae is used to find the $\left[\mathrm{OH}^{-}\right]$ion concentration of a weak monoacidic base?

Rate law for the reaction $a A+b B \rightarrow c C+d D$ is $\mathrm{r}=\mathrm{k}[\mathrm{A}][\mathrm{B}]$. Which from following conditions does NOT affect the rate of reaction?

Identify the name of reaction of aryl halide with alkyl halide and sodium metal in dry ether to give substituted aromatic compounds.

What type of arenes are obtained when arene diazonium chloride is treated with fluoroboric acid and then heated further?

Identify an antiseptic compound from following.

If $\mathrm{E}^{\circ}\left(\mathrm{Ag}^{+}{ }_{(\mathrm{aq})} \mid \mathrm{Ag}_{(\mathrm{s})}\right)=+0.80 \mathrm{~V}$ What is potential developed for $\mathrm{Ag}_{(\mathrm{s})} \longrightarrow \mathrm{Ag}^{+1}(0.01 \mathrm{M})+\mathrm{e}^{-}$at 298 K ?

Calculate the boiling point elevation of solution if 15 g urea is dissolved in 1000 g water. $\left[\mathrm{K}_{\mathrm{b}}\right.$ for water $=0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$; molar mass of urea $=60 \mathrm{~g} \mathrm{~mol}^{-1}$ ]

Identify the product when ethylbenzene reacts with dil nitric acid.

Nitric oxide reacts with $\mathrm{H}_2$ according to reaction, $2 \mathrm{NO}_{(\mathrm{g})}+2 \mathrm{H}_{2(\mathrm{~g})} \longrightarrow \mathrm{N}_{2(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(\mathrm{g})}$, identify the correct relationship among the following.

Which from following compounds is obtained when acetamide is warmed with bromine and excess conc. $\mathrm{KOH}_{(\mathrm{aq})}$ solution?

What is the total number of moles of ' C ' atoms and ' H ' atoms respectively present in following n mole molecule?

Which of the following relations about $\mathrm{E}_{\text {cell }}^{\circ}$ is false?

Arrange the following solutions according to decreasing order of osmotic pressure under similar condition of temperature and assuming complete dissociation.

$$ \begin{array}{|c|l|} \hline \text { I. } & 0.2 \mathrm{~m} \mathrm{KCl} \\ \hline \text { II. } & 0.3 \mathrm{~m} \mathrm{MgSO}_4 \\ \hline \text { III. } & 0.1 \mathrm{~m} \mathrm{BaCl}_2 \\ \hline \text { IV. } & 0.5 \mathrm{~m} \mathrm{Al}_2\left(\mathrm{SO}_4\right)_3 \\ \hline \end{array} $$

Which from following statements is NOT true about isotopes?

$$ \text { Identify the product in the following reaction. } $$

A monobasic weak acid dissociates to $1.2 \%$ in its 0.01 M solution at 298 K . Calculate dissociation constant of it.

The solubility of calcium carbonate at 298 K is $6.4 \times 10^{-5} \mathrm{~mol} \mathrm{dm}^{-3}$. Calculate the value of solubility product at the same temperature?

Which from following represents the Freundlich's empirical equation for adsorption of gas on solid (for $\mathrm{n}>1$ )?

Identify the use of glyptal.

Which from following on hydrolysis forms invert sugar?

Which from following is the general formula of compound obtained when lanthanoid (Ln) reacts with carbon at elevated temperature?

Identify correct statement for the reaction.

$$ \mathrm{I}_2+\mathrm{KClO}_3 \xrightarrow{\Delta} \mathrm{ICl}+\mathrm{KIO}_3 $$

Calculate the number of atoms present per unit cell if product of density and volume of unit cell is $1.8 \times 10^{-22} \mathrm{~g}$.

[Mass of an atom $=4.5 \times 10^{-23} \mathrm{~g}$ ]

Calculate the change in internal energy of the system if 25 kJ of work done by the system and it absorbs 10 kJ of heat.

$$ \text { Identify ' } Z \text { ' in the following reaction. } $$

What is the number of electrons transferred considering Mn when $\mathrm{KMnO}_4$ is converted into $\mathrm{Mn}_2 \mathrm{O}_3$ ?

Identify sequential reactions involved in Sol-Gel process.

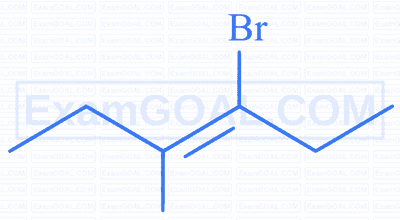
$$ \text { What is IUPAC name of following compound? } $$

What is the number of moles of silver chloride precipitated when excess silver nitrate is treated with one mole of pentaamminecarbonatocobalt (III) chloride?

The mass of $4.48 \mathrm{dm}^3$ of certain gas is 5.6 g at STP. Assuming ideal behaviour, identify the probable gas from following.

Identify the defect developed when an ion of an ionic compound is missing from its regular site and occupies interstitial position between lattice points.

Identify from following an example of intensive property?

Methyl propanoate on hydrolysis with dil NaOH forms a salt that on further acidification with conc. HCl forms

Which from following elements form superoxide with air?

Identify a copolymer from following.

Calculate the number of $\mathrm{Ca}^{2+}$ ion in 222 g anhydrous calcium chloride? (At. Mass $\mathrm{Ca}=40, \mathrm{Cl}=35.5$ )

For a reaction, $\mathrm{A} \longrightarrow \mathrm{B}$, rate equation is $\mathrm{r}=\mathrm{k}[\mathrm{A}]^{\circ}$. If initial concentration of reactant is 'a'mol dm ${ }^{-3}$ find half life time of reaction.

Which of the following compounds is formed as major product in the following reaction.

2-Methylbut-2-ene $\xrightarrow[\text { Peroxide }]{\mathrm{HBr}}$ Product

Which from following cations forms least stable complex with same ligand?

Which of the following species is not tetrahedral?

For cell reaction,

$$ 2 \mathrm{Al}_{(\mathrm{s})}+3 \mathrm{Cu}_{(\mathrm{aq})}^{+2} \longrightarrow 2 \mathrm{Al}_{(\mathrm{aq})}^{+3}+3 \mathrm{Cu}_{(\mathrm{s})} $$

If $\Delta \mathrm{G}^{\circ}=-1158 \mathrm{~kJ}$, what is $\mathrm{E}_{\text {cell }}^{\circ}$?

Calculate the relative lowering of vapour pressure of solution containing 0.56 g nonvolatile solute in 100 g water [molar mass of solute $=60 \mathrm{~g} \mathrm{~mol}^{-1}$ ]

Which among the following has highest boiling point?

Numbers are selected at random, one at a time from the two-digit numbers $00,01,02,-------, 99$ with replacement. An event E occurs only if the product of the two digits of a selected number is 24. If four numbers are selected, then probability, that the event E occurs at least 3 times, is

A particular solution of $3 \mathrm{e}^x \tan y \mathrm{~d} x+\left(1-\mathrm{e}^x\right) \sec ^2 y \mathrm{~d} y=0$ with $y(1)=\frac{\pi}{4}$ is

$\overline{\mathrm{a}}, \overline{\mathrm{b}}, \overline{\mathrm{c}}$ are nonzero vectors such that $\overline{\mathrm{a}}$ is perpendicular to $\overline{\mathrm{b}}$ and $\overline{\mathrm{c}},|\overline{\mathrm{a}}|=1,|\overline{\mathrm{~b}}|=2,|\overline{\mathrm{c}}|=1$ and $\overline{\mathrm{b}} \cdot \overline{\mathrm{c}}=1$. There is nonzero vector $\overline{\mathrm{d}}$ coplanar with $\overline{\mathrm{a}}+\overline{\mathrm{b}}$ and $2 \overline{\mathrm{~b}}-\overline{\mathrm{c}}$. If $\overline{\mathrm{d}} \cdot \overline{\mathrm{a}}=1$, then $|\overline{\mathrm{d}}|^2=$

If $\sin ^{-1} x+\sin ^{-1} y=\frac{\pi}{3}$ and $\cot ^{-1}\left(\frac{1}{x}\right)-\cot ^{-1}\left(\frac{1}{y}\right)=0$ then $2 x^2+y^2-x y=$ $\qquad$

The value of $\sin \left[\tan ^{-1}\left(\frac{1-x^2}{2 x}\right)+\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\right]$ is

The area of the region bounded by the curve $y=|x-2|$ between $x=1, x=3$ and X -axis is ……

$$ \int_{-1}^3\left(\tan ^{-1}\left(\frac{x}{x^2+1}\right)+\tan ^{-1}\left(\frac{x^2+1}{x}\right)\right) d x= $$

Let A be a non-singular matrix of order n and $|A|=k$, then $(\operatorname{adj} A)^{-1}$ is

If $f(x)= \begin{cases}\frac{8^x-4^x-2^x+1^x}{x^2}, & \text { if } x>0 \\ \mathrm{e}^x \sin x+\mathrm{i} x+\lambda \log 4, & \text { if } x \leqslant 0, \mathrm{i} \in \mathbb{R}\end{cases}$ continuous at $x=0$, then the value of $500 \mathrm{e}^\lambda$ is

The line passing through the point $(5,1, a)$ and $(3, \mathrm{~b}, 1)$ crosses the $y \mathrm{z}$-plane at $\left(0, \frac{17}{2}, \frac{-13}{2}\right)$, then the value of $2 a+3 b$ is

The direction ratios of the line of intersection of the planes $x-y+z-5=0$ and $x-3 y-6=0$, are

The distance between the line $\overline{\mathrm{r}}=3 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\hat{\mathrm{k}}+\lambda(\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})$ and the plane $\overline{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})=4$ is

If $y=\sin ^2\left(\cot ^{-1}\left(\sqrt{\frac{1-x}{1+x}}\right)\right)$, then $\frac{\mathrm{d} y}{\mathrm{~d} x}=$

$$ \int \frac{\sin x}{\sqrt{5 \sin ^2 x+6 \cos ^2 x}} d x $$

If $\mathrm{f}(x)=\frac{\mathrm{k} \sin x+2 \cos x}{\sin x+\cos x}$ is strictly increasing for all real values of $x$, then

The locus of the points represented by $|z+3|-|z-3|=6$, where $z$ is a complex number, is ….

The locus of point of intersection of the tangents to the circle $x^2+y^2=16$, such that the angle between them is $60^{\circ}$, is

A random variable, $X$ has p.m.f. $\mathrm{P}(\mathrm{X}=x)=\frac{{ }^4 \mathrm{C}_x}{2^4}, x=0,1,2,3,4$ and $\mu$ and $\sigma^2$ are mean and variance respectively of random variable X , then

$$ \text { The c.d.f. of a discrete random variable } \mathrm{X} \text { is } $$

$$ \begin{array}{|c|c|c|c|c|c|c|c|c|} \hline \mathrm{X} & -3 & -1 & 0 & 1 & 3 & 5 & 7 & 9 \\ \hline \mathrm{~F}(\mathrm{X}=x) & 0.1 & 0.3 & 0.5 & 0.65 & 0.75 & 0.85 & 0.90 & 1 \\ \hline \end{array} $$

Then $\frac{P[X=-3]}{P[X<0]}=$

The distance between the lines represented by $16 x^2+9 y^2+48 x-24 x y-36 y+35=0$ is ......... units

The value of $\tan 20^{\circ} \tan 80^{\circ} \cot 50^{\circ}=$

The equation of the curve passing through the origin and satisfying the equation $\left(1+x^2\right) \frac{\mathrm{d} y}{\mathrm{~d} x}+2 x y=4 x^2$, is

The value of $m \in \mathbb{R}$, when angle between the vectors $\overline{\mathrm{p}}=\mathrm{m} y \hat{\mathrm{i}}-6 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$ and $\overline{\mathrm{q}}=y \hat{\mathrm{i}}+2 \hat{\mathrm{j}}+2 \mathrm{~m} y \hat{\mathrm{k}}$ is obtuse angle, is

The volume of the tetrahedron whose coterminous edges are represented by

$$ \bar{a}=-12 \hat{i}+p \hat{k}, \bar{b}=3 \hat{j},-\hat{k}, \bar{c}=2 \hat{i}+\hat{j}-15 \hat{k} $$

570 cu. units, then $\mathrm{p}=$

With usual notations, the perimeter of a triangle ABC is 6 times the arithmetic mean of sine of its angles. If $\mathrm{a}=1$, then $\angle \mathrm{A}=$

The angle between the lines whose direction cosines are $\frac{-\sqrt{3}}{4}, \frac{1}{4}, \frac{-\sqrt{3}}{2}$ and $\frac{-\sqrt{3}}{4}, \frac{1}{4}, \frac{\sqrt{3}}{2}$ is

If $\sin \left(\frac{\pi}{4} \cot \theta\right)=\cos \left(\frac{\pi}{4} \tan \theta\right)$, then the general solution of $\theta$ is

The differential equation of all circles having their centres on the line $y=5$ and touching ( X -axis) is $\qquad$

$$ \int_0^{\frac{\pi}{4}} \frac{\cos ^2 x \sin ^2 x}{\cos ^3 x+\sin ^3 x} d x= $$

If $\{(\mathrm{p} \wedge \sim \mathrm{q}) \wedge(\mathrm{p} \wedge \mathrm{r})\} \rightarrow \sim \mathrm{p} \vee \mathrm{q}$ has truth value false then truth values of the statements $p, q, r$ are respectively

In a triangle ABC , with usual notations, $\tan \left(\frac{\mathrm{A}}{2}\right)=\frac{5}{6}, \tan \left(\frac{\mathrm{C}}{2}\right)=\frac{2}{5}$, then

If ${ }^{n+4} C_{n+1}-{ }^{n+3} C_n=15(n+2)$, then $n=$

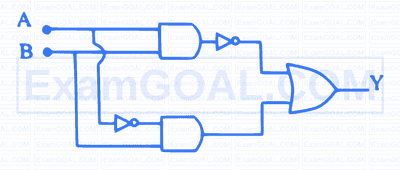
The correct simplified circuit diagram for the logical statement $[\{\mathrm{q} \wedge(\sim \mathrm{q} \vee \mathrm{r})\} \wedge\{\sim \mathrm{p} \vee(\mathrm{p} \wedge \sim \mathrm{r})\}] \vee(\mathrm{p} \wedge \mathrm{r})$ Where $p, q, r$ represents switches $s_1, s_2, s_3$ respectively.

$$ \mathop {\lim }\limits_{n \to \infty }\left[\frac{1}{1-n^4}+\frac{8}{1-n^4}+\ldots \ldots \ldots \ldots .+\frac{n^3}{1-n^4}\right]= $$

If $f(\theta)=\cos \theta_1 \cdot \cos \theta_2 \cdot \cos \theta_3$ .............. $\cos \theta_n$, then $\tan \theta_1+\tan \theta_2+\tan \theta_3+$. ............ $+\tan \theta_{\mathrm{n}}=$

The length of the altitude through the point $D$ of tetrahedron where the vertices of the tetrahedron are $A(2,3,1), B(4,1,-2), C(6,3,7), D(-5,-4,8)$, is

The angle between the lines $\frac{x-1}{l}=\frac{y+1}{m}=\frac{z}{n}$ and $\frac{x+1}{\mathrm{~m}}=\frac{y-3}{\mathrm{n}}=\frac{\mathrm{z}-1}{l}$, where $l>\mathrm{m}>\mathrm{n}$ and $1, \mathrm{~m}, \mathrm{n}$ are roots of the equation $x^3+x^2-4 x-4=0$, is

The distance of the point $\mathrm{P}(3,8,2)$ from the line $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z-2}{3}$ measured parallel to the plane $3 x+2 y-2 z+15=0$ is

The solution set for minimizing the function $\mathrm{z}=x+y$ with constraints $x+y \geqslant 2, x+2 y \leqslant 8, y \leqslant 3, x, y \geqslant 0$ contains

The abscissae of the points of the curve $y=x^3$ are in the interval $[-2,2]$, where the slope of the tangents can be obtained by mean value theorem for the interval $[-2,2]$ are

Let $x$ be the length of each of the equal sides of an isosceles triangle and $\theta$ be the angle between these sides. If $x$ is increasing at the rate $\frac{1}{12} \mathrm{~m} /$ hour and $\theta$ is increasing at the rate $\frac{\pi}{180} \mathrm{rad} /$ hour, then the rate at which area of the triangle is increasing when $x=12 \mathrm{~m}$ and $\theta=\frac{\pi}{4}$ is

$$ \int \cos \left(\frac{x}{16}\right) \cdot \cos \left(\frac{x}{8}\right) \cdot \cos \left(\frac{x}{4}\right) \cdot \sin \left(\frac{x}{16}\right) \mathrm{d} x= $$

$$ \int \frac{x^3}{(x+1)^2} d x= $$

A wire of length 8 units is cut into two parts which are bent respectively in the form of a square and a circle. The least value of the sum of the areas so formed is

If $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are mutually exclusive and exhaustive events of a sample space $S$ such that $P(B)=\frac{3}{2} P(A)$ and $P(C)=\frac{1}{2} P(B)$, then $P(A)=$

Angle between the parabola $y^2=4(x-1)$ and $x^2+4(y-3)=0$ at the common end of their latus rectum is

The points $(1,3)$ and $(5,1)$ are two opposite vertices of a rectangle. The other two vertices are lie on the line $y=2 x+\mathrm{c}$ where c is the constant, then co-ordinates of other two vertices are

If $y=\mathrm{a}^x \cdot \mathrm{~b}^{2 x-1}$, then $\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}$ is equal to

In a culture bacteria count is $1,00,000$ initially. The number increases by $10 \%$ in first 2 hours. In how many hours will the count reach $2,00,000$, if the rate of growth of bacteria is proportional to the number present?

Error in the measurement of radius of the sphere is $2 \%$. The error in the calculated value of its volume is

In the circuit shown in the figure, $P \neq R$. The reading of the galvanometer remains the same with switch ' $S$ ' open or closed. Then

A unit vector in the direction of resultant vector of $\vec{A}=-2 \hat{i}+3 \hat{j}+\hat{k}$ and $\vec{B}=\hat{i}+2 \hat{j}-4 \hat{k}$ is

The moment of inertia of a ring about an axis passing through its centre and perpendicular to its plane is I. It is rotating with angular velocity $\omega$. Another identical ring is gently placed on it so that their centres coincide. If both the rings are rotating about the same axis then loss in kinetic energy is

The two coherent sources produce interference with intensity ratio ' $b$ '. In the interference pattern, the ratio $\frac{I_{\text {max }}+I_{\text {min }}}{I_{\text {max }}-I_{\text {min }}}$ will be

The radii of circular orbits of two satellites $A$ and $B$ of the earth are ' $4 R$ ' and ' $R$ ' respectively, where $R$ is the radius of earth. If the speed of satellite $B$ is 6 V , then the speed of satellite $A$ will be

The space within the current carrying toroid is filled with aluminium of susceptibility ' $\chi$ '. The percentage increase in the magnetic field ' $B$ ' will be

Using Bohr's quantization condition, the rotational kinetic energy in the third orbit for a diatomic molecule is ( $h=$ Planck's constant, $\mathrm{I}=$ moment of inertia of diatomic molecule)

A body is rotating about its own axis. Its rotational kinetic energy is ' x ' and its angular momentum is ' $y$ '. Hence its moment of inertia about its own axis is

A ray of light travelling through rarer medium is incident at a very small angle ' $i$ ' on a glass slab and after refraction its velocity is reduced by $20 \%$. The angle of deviation is

A body starts from rest and moves with a uniform acceleration. The ratio of the distance covered by the body in the $n^{\text {th }}$ second of its motion to the total distance travelled in n second is

A coil is wound on a core of rectangular crosssection. If all the linear dimensions of core are increased by a factor 3 and number of turns per unit length of coil remains same, the selfinductance increases by a factor

In air, a charged soap bubble of radius R breaks into 64 small soap bubbles of equal radius $r$. The ratio of mechanical force per unit area of big soap bubble to that of a small bubble is

When photons of energies twice and thrice the work function of a metal are incident on the metal surface one after other, the maximum velocities of the photoelectrons emitted in the two cases are $V_1$ and $V_2$ respectively. The ratio $\mathrm{V}_1: \mathrm{V}_2$ is

According to Huygen's wave theory of light, which one of the following statements is not correct?

A conveyor belt is moving with constant velocity (V). Sand is being dropped on the belt at the rate of $\mathrm{M} \mathrm{kg} / \mathrm{s}$. The force necessary to keep the belt moving with a constant velocity $\mathrm{V} \mathrm{m} / \mathrm{s}$ will be

A coil having 9 turns carrying current produces magnetic field $B_1$ at the centre. Now that coil is rewounded into 3 turns carrying same current. Then magnetic field at the centre $B_2$ is

Two capillary tubes of same diameter are kept vertically in two liquids whose densities are in the ratio $4: 3$. If their surface tensions are in the ratio $6: 5$, the ratio of heights $\left(\frac{h_1}{h_2}\right)$ of liquids in the two capillary tubes is (Their angle of contacts are same)

An ideal inductor of $\left(\frac{1}{\pi}\right) \mathrm{H}$ is connected in series with a $300 \Omega$ resistor. If a $20 \mathrm{~V}, 200 \mathrm{~Hz}$ alternating source is connected across the combination, the phase difference between the voltage and current is

Hot water cools from $80^{\circ} \mathrm{C}$ to $60^{\circ} \mathrm{C}$ in 1 minutes. In cooling from $60^{\circ} \mathrm{C}$ to $50^{\circ} \mathrm{C}$ it will take (room temperature $=30^{\circ} \mathrm{C}$ )

A Carnot engine has efficiency $\frac{1}{6}$. It becomes $\frac{1}{3}$, when the temperature of $\operatorname{sink}$ is lowered by

57 K . The temperature of the source is

An alternating e.m.f. having voltage $\mathrm{V}=\mathrm{V}_0 \sin \omega t$ is applied to a series L-C-R circuit. Given : $\left|X_L-X_C\right|=R$. The r.m.s. value of potential difference across capacitor will be

A simple pendulum oscillates with an angular amplitude $\theta$. If the maximum tension in the string is 4 times the minimum tension then the value of $\theta$ is

An electron moves in Bohr orbit. The magnetic field at the centre is proportional to

The r.m.s. speed of gas molecules at 800 K will be

If the charge on the capacitor is increased by 3C, the energy stored in it increases by $21 \%$. The original charge on the capacitor is

In the following combination of logic gates, the output $Y$ can be written in the terms of inputs $A$ and B as

If a black body at 400 K surrounded by atmosphere at 300 K has rate of cooling ' $\mathrm{R}_0$ ', the same body at 900 K , surrounded by same atmosphere, will have rate of cooling nearly

The electric field intensity on the surface of a solid charged sphere of radius $\mathbf{r}$ and volume charge density $\sigma$ is ( $\varepsilon_0=$ permittivity of free space)

Two strings ' X ' and ' Y ' of a guitar produces a beat frequency of 6 Hz . When the tension of the string ' Y ' is increased, the beat frequency is found to be 4 Hz . If the frequency of string ' X ' is 300 Hz , then the original frequency of string ' Y ' is

In common emitter mode of a transistor, the current gain is 8 . The input impedance is $25 \mathrm{k} \Omega$ and load resistance is $75 \mathrm{k} \Omega$. The power gain is

A transverse displacement of vibrating string is $y=0.06 \sin \left(\frac{2 \pi}{3}\right) \times \cos (120 \pi t)$.

If the mass per unit length of a string is $4 \times 10^{-2} \mathrm{~kg} / \mathrm{m}$, then the tension in the string will be

The equation of a progressive wave is $\mathrm{Y}=3 \sin \left[\pi\left(\frac{\mathrm{t}}{3}-\frac{\mathrm{x}}{5}\right)+\frac{\pi}{4}\right]$ where x and y are in meter and time in second. Which of the following is correct?

If the internal resistance of cell is negligible then current flowing through the circuit is

Water flows through a horizontal pipe of varying cross-section at the rate of $\pi \times 10^{-1} \mathrm{~m} / \mathrm{s}$. The velocity of water at a point where the radius of the pipe is 10 cm is $(\pi=3.14)$

In an electrical circuit ' $R$ ', ' $L$ ', ' $C$ ' and an a.c. voltage source are all connected in series. When ' L ' is removed from the circuit, the phase difference between the voltage and the current in the circuit is $\frac{\pi}{3}$. If instead ' $C$ ' is removed from the circuit, the phase difference is again $\frac{\pi}{3}$. The power factor of the circuit is $\left(\tan \frac{\pi}{3}=\sqrt{3}\right)$

A parallel plate capacitor having plate area ' $A$ ' and separation ' $d$ ' is charged to a potential difference ' $V$ '. The charging battery is disconnected and the plates are pulled apart to four times the initial separation. The work required to increase the distance between the plates is ( $\varepsilon_0=$ permittivity of free space)

The length of the simple pendulum is made 3 times the original length. If ' T ' is its original time period, then the new time period will be

A plano convex lens fits exactly in to a plano concave lens. Their plane surfaces are parallel to each other. Lenses are made up of different materials of refractive indices ' $\mathrm{n}_1$ ' ' $\mathrm{n}_2$ ' and ' R ' is the radius of curvature of the curved surface of lenses. Focal length of the combination is

Moment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is ' $I$ '. If the same rod is bent in the form of ring, its moment of inertia about the diameter is ' $\mathrm{I}_1$ '. If $\mathrm{I}_1=\mathrm{xI}$, then the value of ' x ' is

If an ammeter is to be used in place of a galvanometer then we must connect

The temperature of an ideal gas is increased from 100 K to 400 K . If ' $x$ ' is the R.M.S. velocity of its molecules at 100 K , it becomes

What is the phase difference between the flux linked with a coil rotating in a uniform magnetic field and the induced e.m.f. produced in it?

A pendulum bob has a speed $4 \mathrm{~m} / \mathrm{s}$ at its lowest position. The pendulum is 1 m long. When the length of the string makes an angle of $60^{\circ}$ with the vertical, the speed of the bob at that position is (acceleration due to gravity, $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2$, $\cos 60^{\circ}=0.5$ )

A vehicle starts from rest and accelerates along straight path at $2 \mathrm{~m} / \mathrm{s}^2$. At the starting point of the vehicle, there is a stationary electric siren. How far has the vehicle nearly gone when the driver hears the siren at $94 \%$ of its value when the vehicle was at rest?

(speed of sound $=220 \mathrm{~m} / \mathrm{s}$ )

When a light of wavelength $\lambda$ falls on the emitter of a photocell, maximum speed of emitted photoelectrons is V . If the incident wavelength is changed to $\frac{2 \lambda}{3}$, maximum speed of emitted photoelectrons will be :

A parallel plate capacitor has plate area $50 \mathrm{~cm}^2$ and plate separation 3 mm . The space between the plates is filled with a dielectric medium of thickness 1 mm and dielectric constant 4 . The capacitance becomes ( $\varepsilon_0=$ permittivity of free space)

Heat is given to an ideal gas in an isothermal process. Then

A. internal energy of the gas will decrease.

B. internal energy of the gas will increase.

C. internal energy of the gas will not change.

D. the gas will do negative work.

Two long parallel wires carry currents $I_1$ and $\mathrm{I}_2\left(\mathrm{I}_1>\mathrm{I}_2\right)$. When currents are flowing in the same direction, the magnetic field at a point midway between the wires is $6 \times 10^{-6} \mathrm{~T}$. If the direction of $\mathrm{I}_2$ is reversed the field at midpoint becomes $3 \times 10^{-5} \mathrm{~T}$. The ratio $\mathrm{I}_1: \mathrm{I}_2$ is