WB JEE 2008 | Gravitation Question 2 | Physics

WB JEE 2008

MCQ (Single Correct Answer)

-0.25

The weight of a body on surface of earth is 12.6 N. When it is raised to a height half the radius of earth, its weight will be

2.8 N

5.6 N

12.6 N

25.2 N

WB JEE 2024

MCQ (Single Correct Answer)

-0.25

A satellite of mass $$\mathrm{m}$$ rotates round the earth in a circular orbit of radius R. If the angular momentum of the satellite is J, then its kinetic energy $$(\mathrm{K})$$ and the total energy (E) of the satellite are

$$\mathrm{K}=\frac{\mathrm{J}^2}{\mathrm{mR}^2}, \mathrm{E}=-\frac{\mathrm{J}^2}{2 \mathrm{mR}^2}$$

$$\mathrm{K}=\frac{\mathrm{J}^2}{2 \mathrm{mR}^2}, \mathrm{E}=-\frac{\mathrm{J}^2}{2 \mathrm{mR}^2}$$

$$\mathrm{K}=\frac{\mathrm{J}^2}{2 \mathrm{mR}^2}, \mathrm{E}=-\frac{\mathrm{J}^2}{\mathrm{mR}^2}$$

$$K=\frac{J^2}{2 \mathrm{mR}^2}, E=\frac{J^2}{\mathrm{mR}^2}$$

WB JEE 2023

MCQ (Single Correct Answer)

-0.25

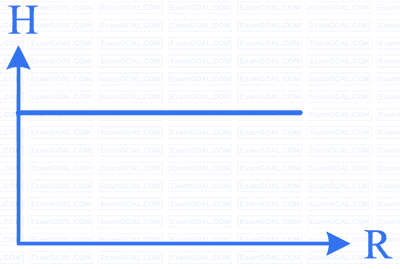
Acceleration due to gravity at a height H from the surface of a planet is the same as that at a depth of H below the surface. If R be the radius of the planet, then H vs. R graph for different planets will be,

WB JEE 2023 Physics - Gravitation Question 2 English Option 1

WB JEE 2023 Physics - Gravitation Question 2 English Option 2

WB JEE 2023

MCQ (Single Correct Answer)

-0.5

An earth's satellite near the surface of the earth takes about 90 min per revolution. A satellite orbiting the moon also takes about $$90 \mathrm{~min}$$ per revolution. Then which of the following is true?

[where $$\rho_{\mathrm{m}}$$ is density of the moon and $$\rho_{\mathrm{e}}$$ is density of the earth.]

$$\rho_{\mathrm{m}}<\rho_{\mathrm{e}}$$

$$\rho_{m}>\rho_{e}$$

$$\rho_{m}=\rho_{e}$$

No conclusion can be made about the densities.

PREVIOUS NEXT

WB JEE Subjects