Assume the cell reaction,

$$ \mathrm{A}_{(\mathrm{s})}+\mathrm{B}_{(\mathrm{aq})}^{+2} \longrightarrow \mathrm{~A}_{(\mathrm{aq})}^{+2}+\mathrm{B}_{(\mathrm{s})} $$

if $\Delta \mathrm{G}^{\circ}=-386 \mathrm{~kJ}$ at 298 K . What is $\mathrm{E}_{\mathrm{Cell}}^0$ ?

Calculate the volume occupied by a particle in bcc unit cell if the volume of unit cell is $8.2 \times 10^{-23} \mathrm{~cm}^3$.

Identify the name of reaction for aryl halide with alkyl halide and sodium metal in dry ether to give substituted aromatic compounds.

Which among the following compounds forms pink colouration on addition of Schiff's reagent?

Calculate work done if 1 mole of an ideal gas compressed isothermally and reversibly from 12 $\mathrm{dm}^3$ to $6 \mathrm{dm}^3$ at $300 \mathrm{~K} .\left[\mathrm{R}=8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}\right]$

Calculate the number of unit cells in $1 \mathrm{~cm}^3$ volume of an element if unit cell edge length is $4.0 \times 10^{-8} \mathrm{~cm}$.

Which from following compounds contains complex cations and anions?

If concentration of reactant ' $A$ ' is increased by 10 times, rate of reaction increases 100 times. What is order of reaction if rate law is $r=k[A]^r$ ?

Which from following lanthanoids exhibits +4 oxidation state in $\mathrm{F}^7$ configuration?

Which among the following salts turns red litmus blue in its aqueous solution?

A container consisting mixture of $28 \mathrm{~g} \mathrm{~N}_2, 8 \mathrm{~g} \mathrm{He}$ and 40 g Ne at $25^{\circ} \mathrm{C}$. If the total pressure exerted by the gaseous mixture is 20 bar , What is the partial pressure exerted by $\mathrm{N}_2$ ?

Select the incorrect statement about $\mathrm{N}_2$ molecule.

Identify the correct decreasing order of boiling point for hydrides of halogens.

Find out number of carbon atoms present in 0.35 mole of glucose.

Find the expected value of $\Delta \mathrm{T}_{\mathrm{b}}$ for $1 \mathrm{~m} \mathrm{AlCl}{ }_3$ solution in water if solution of nonelectrolyte of same concentration has $\Delta \mathrm{T}_{\mathrm{b}}$ value ' $x$ ' K .

Which of the following change takes place at positive electrode during working of dry cell?

4 gram of NaOH is added in water to form 500 mL solution at 298 K . What is pH of solution? (Molar mass of $\mathrm{NaOH}=40 \mathrm{~g} \mathrm{~mol}^{-1}$ )

A compound contains atoms of $x, y$ and z elements. Oxidation numbers of $x, y$ and $z$ are +3 , +5 and -2 respectively. Identify the possible formula of this compound.

Which of the following compound is used for preparation of quicklime?

Which from following gases is adsorbed to greater extent if adsorbent remains same at similar conditions of temperature and pressure?

Which of the following is effectively used to remove E. coli bacteria from water?

What is order and molecularity of following reaction?

$$ \mathrm{NO}_{2(\mathrm{~g})}+\mathrm{NO}_{2(\mathrm{~g})} \longrightarrow 2 \mathrm{NO}_{(\mathrm{g})}+\mathrm{O}_{2(\mathrm{~g})} $$

The solubility of salt $\mathrm{BA}_2$ is $4 \times 10^{-4} \mathrm{~mol} \mathrm{dm}^{-3}$.

What is solubility product of the salt?

Which among the following compounds has lowest boiling point?

What is shape of $\mathrm{BrF}_5$ molecule?

The correct order of reactivity for reaction involving cleavage of C-X bond in following compounds is

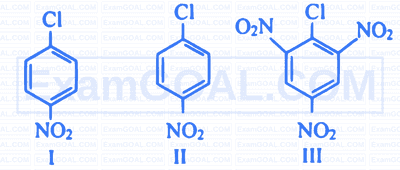
Which from following is a strong field ligand?

Calculate vapour pressure of pure volatile liquid $B$ at given temperature if mole faction of liquid $B$ and vapour pressure of pure volatile liquid $A$ are 0.4 and 400 mm Hg respectively.

$$ \left[\mathrm{P}_{\text {total }}=600 \mathrm{~mm} \mathrm{Hg}\right] $$

Identify the monomer used in preparation of polyacrylonitrile?

Identify the product ' B ' in following reaction.

Ethanal $\xrightarrow{\text { dil } \mathrm{NaOH}} A \xrightarrow[\mathrm{H}_2 \mathrm{O}]{\Delta} B$

What are the positions of ' N ' atoms present in pyrimidine ring of nucleic acids?

Identify the major product obtained when anisole reacts with bromine in acetic acid.

Calculate the molality of nonvolatile solution if solution freezes at $-0.95^{\circ} \mathrm{C}$

$\left[K_f\right.$ for water, $=1.86 \mathrm{~K} \mathrm{~mol}^{-1}$, freezing point of water $=0^{\circ} \mathrm{C}$ ]

Which from following is the most stable species?

Half life of a first order reaction is 3 minute. What is the time required to reduce the concentration of reactant by $90 \%$ of its initial concentration?

Identify neutral amino acid from following list represented by three letter symbols.

Which from following statement is correct regarding emf of cell for the cell reaction,

$$ \mathrm{Cd}_{(\mathrm{s})}+\mathrm{Cu}_{(\mathrm{aq})}^{+2} \longrightarrow \mathrm{Cd}_{(\mathrm{aq})}^{+2}+\mathrm{Cu}_{(\mathrm{s})} $$

if concentration of $\mathrm{Cd}^{+2}$ is 10 times greater than concentration of $\mathrm{Cu}_{(\mathrm{aq})}^{+2}$ at 298 K .

Which from following polymers when blended with cotton develops terycot?

Which from following compounds is an example of secondary amine?

Which cation from following develops least magnetic moment?

Identify false statement regarding aspirin.

Which from following compounds has highest boiling point?

Which of the following dopants is used in germanium to form n-type semiconductor?

Identify from following physical transformations that exhibits decrease in entropy.

"No two electrons in an atom can have the identical set of four quantum numbers." The statement is known as

Which among the following functional groups is reduced by diborane?

What it the IUPAC name of following compounds?

Identify the substrate ' S ' in the following reaction,

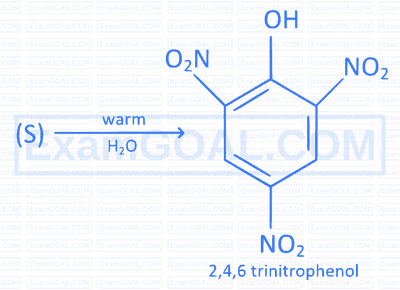
Propene on hydroboration followed by oxidation with alkaline peroxide forms.

Calculate the standard enthalpy change of following reaction.

$$ \mathrm{C}_2 \mathrm{H}_{4(\mathrm{~g})}+3 \mathrm{O}_{2(\mathrm{~g})} \longrightarrow 2 \mathrm{CO}_{2(\mathrm{~g})}+2 \mathrm{H}_2 \mathrm{O}_{(l)} $$

If $\Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{C}_2 \mathrm{H}_4\right)=-52 \mathrm{~kJ} \mathrm{~mol}^{-1}$

$$ \begin{aligned} & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{CO}_2\right)=-390 \mathrm{~kJ} \mathrm{~mol}^{-1} \\ & \Delta_{\mathrm{f}} \mathrm{H}^{\circ}\left(\mathrm{H}_2 \mathrm{O}\right)=-286 \mathrm{~kJ} \mathrm{~mol}^{-1} \end{aligned} $$

If $3 \sin 2 \theta=2 \sin 3 \theta$ and $0<\theta<\pi$, then the value of $\sin \theta$ is equal to

The number of integral values of $k$ for which $x^2+y^2+\mathrm{k} x+(1-\mathrm{k}) y+5=0$ represents a circle whose radius cannot exceeds 5 , are

In a triangle ABC with usual notations if $|\overline{\mathrm{BC}}|=8,|\overline{\mathrm{CA}}|=7,|\overline{\mathrm{AB}}|=10$ then the projection of $\overline{\mathrm{AB}}$ on $\overline{\mathrm{AC}}$ is

If $\bar{a}=\hat{i}+\hat{j}, \bar{b}=2 \hat{i}-\hat{k}$ then the point of intersection of the lines $\overline{\mathrm{r}} \times \overline{\mathrm{a}}=\overline{\mathrm{b}} \times \overline{\mathrm{a}}$ and $\overline{\mathrm{r}} \times \overline{\mathrm{b}}=\overline{\mathrm{a}} \times \overline{\mathrm{b}}$ is

A scholarship amount is given by $\mathrm{z}=550 x+300 y$ and is to be distributed among $x$ boys and $y$ girls. From the graph given below the maximum amount of scholarship is __________

$$ \int \log (2+x)^{2+x} d x= $$

If the projection of $\bar{a}$ on $\bar{b}+\bar{c}$ is twice the projection of $\bar{b}+\bar{c}$ on $\bar{a}$ also if $|\bar{b}|=2 \sqrt{2},|\bar{c}|=4$ and the angle between $\overline{\mathrm{b}}$ and $\overline{\mathrm{c}}$ is $\frac{\pi}{4}$ then $|\overline{\mathrm{a}}|=$

The equation of the plane passing through the point of intersection of the planes $2 x-y+z-3=0$ and $4 x-3 y+5 z+9=0$ and parallel to the line $\frac{x+1}{2}=\frac{y+3}{4}=\frac{z-3}{5}$ is $\alpha x+\beta y+\gamma z+d=0$ Then $\alpha+\beta+\gamma+d=$

If the points $\mathrm{A}(1,1,2), \mathrm{B}(2,1, \mathrm{p}), \mathrm{C}(1,0,3)$ and $D(2,2,0)$ are coplanar then the value of $p$ is

$$ \int \frac{\mathrm{e}^{\tan ^{-1} 2 x}}{1+4 x^2}= $$

If the equation of the median through vertex $\mathrm{A}(3, \mathrm{k})$ of $\triangle \mathrm{ABC}$ with vertices $\mathrm{B}(2,1)$ and $\mathrm{C}(-4,5)$ is $x+4 y=\mathrm{p}$, then $\mathrm{k}=$ where p and k are constants

If $\overline{\mathrm{a}}$ and $\overline{\mathrm{b}}$ are unit vectors and $\theta$ is the angle between them, then $\tan \frac{\theta}{2}=$

A manufacturer produces $x$ items per week at a total cost of ₹ $\left(x^2+78 x+2500\right)$. The price per unit is given by $8 x=600-\mathrm{p}$ where ' p ' is the price of each unit. Then the maximum profit obtained is

If the equation $\mathrm{k} x y+10 x+8 y+16=0$ represents a pair of lines, then

If the differential equation $\frac{\mathrm{d} y}{\mathrm{~d} x}+\frac{x}{y}=\frac{\mathrm{a}}{y}$ where a is constant, represents a family of circles then the radius of the circle is $\qquad$

If $2 \mathrm{f}(x)+3 \mathrm{f}\left(\frac{1}{x}\right)=x^2+1, x \neq 0$ and $y=5 x^2 \mathrm{f}(x)$, then $y$ is strictly increasing in

The possible values of $\theta \in(0, \pi)$ such that $\sin \theta+\sin (4 \theta)+\sin (7 \theta)=0$ are

AOB is the positive quadrant of the ellipse $\frac{x^2}{25}+\frac{y^2}{9}=1$ in which $\mathrm{OA}=5, \mathrm{OB}=3$. The area between the arc AB and the chord AB of the ellipse in sq. units is

In a triangle ABC , the sides $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are such that they are the roots of the equation $x^3-11 x^2+38 x-40=0$ Then

$$ \frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}= $$

In a triangle ABC with usual notations if $\mathrm{a}=13$, $b=14, c=15$ Then $\sin A=$

$$ \int_0^3 \frac{d x}{(x+2) \sqrt{x+1}}= $$

If $2 \tan ^{-1}(\cos x)=\tan ^{-1}(2 \operatorname{cosec} x)$, then the value of $x$ is

The particular solution of the differential equation $\cos \left(\frac{d y}{d x}\right)=7, y=1$ at $x=0$ is

In a triangle $A B C$, with usual notations, $3 \mathrm{~b}=\mathrm{a}+\mathrm{c}$, then $\cot \frac{\mathrm{A}}{2} \cdot \cot \frac{\mathrm{C}}{2}=$

$$ \int_0^{\frac{\pi}{2}} \frac{d x}{1+(\cot x)^{101}}= $$

The solution of $\left(1+y^2\right)+\left(x-\mathrm{e}^{\tan ^{-1} y}\right) \frac{\mathrm{d} y}{\mathrm{~d} x}=0$ is

If $\left[\begin{array}{lll}1 & 3 & 3 \\ 1 & 4 & 4 \\ 1 & 3 & 4\end{array}\right]\left[\begin{array}{l}x \\ y \\ z\end{array}\right]=\left[\begin{array}{l}12 \\ 15 \\ 13\end{array}\right]$, then the value of $x^2+y^2+z^2=$

The rate of reduction of a persons assets is proportional to the square root of the existing assets. The assets reduced from 25 lakhs to 6.25 lakhs in 2 years. This rate of reduction of his assets will make him bankrupt in

The distance of the point $(2,4,0)$ from the point of intersection of the lines $\frac{x+6}{3}=\frac{y}{2}=\frac{z+1}{1}$ and $\frac{x-7}{4}=\frac{y-9}{3}=\frac{z-4}{2}$ is

The approximate value of $\cos \left(59^{\circ} 30^{\prime}\right)$ is (given $1^{\circ}=0.0175^{\mathrm{c}}, \sin 60^{\circ}=0.8660$ )

The co-ordinates of the point where the line joining the points $(2,-3,1)$ and $(3,-4,-5)$ and intersects the plane $2 x+y+z=7$ are

$$ \int \mathrm{e}^x \frac{(x-1)}{(x+1)^3} \mathrm{~d} x= $$

If the curve $y=a x^2-6 x+b$ passes through $(0,4)$ and has its tangent parallel to the X-axis at $x=\frac{3}{2}$, then the values of $a$ and $b$ respectively are

The negation of $(p \wedge \sim q) \rightarrow(p \vee \sim q)$ is

If $\mathrm{a}\left(4+x^2\right)=x$ and $y-x^3=\mathrm{a}^2$ then $\frac{\mathrm{d} y}{\mathrm{~d} x}$ at $x=1$ is $\qquad$

The equivalent statement of "If three vertices of a triangle are represented by cube roots of unity, then the triangle is an equilateral triangle" is

$$ f(x)= \begin{cases}{\left[x^2\right]-\left[-x^2\right],} & x \neq 3 \\ k & , x=3\end{cases} $$

is continuous at $x=3$, then $\mathrm{k}=$ where $[\cdot]$ is greatest integer function

$\mathop {\lim }\limits_{x \to 0} \frac{\left(7^x-1\right)^4}{\tan \left(\frac{x}{\mathrm{k}}\right) \cdot \log \left(1+\frac{x^2}{3}\right) \cdot \sin 4 x}=3(\log 7)^3$, then $\mathrm{k}=$

If $x^y+y^x=\mathrm{a}^{\mathrm{b}}$, then $\frac{\mathrm{d} y}{\mathrm{~d} x}$ at $x=1, y=2$ is

The value of $\frac{(\cos \theta+i \sin \theta)^4}{(\sin \theta+i \cos \theta)^5}=$ where $\mathrm{i}=\sqrt{-1}$

If $\mathrm{f}(x)=2 x^3+\mathrm{m} x^2-13 x+\mathrm{n}$ and 2,3 are the roots of the equation $\mathrm{f}(x)=0$ then the value of $4 m+5 n$ is

4 red balls and 5 green balls are selected from $n$ balls. If the sum of both the selections is greater than ${ }^{n+1} C_4$ then the value of $n$ is equal to

Two numbers are selected at random, without replacement from the first 6 positive integers. Let $X$ denote the larger of the two numbers. Then $\mathrm{E}(\mathrm{X})=$

For $\mathrm{k}=1,2,3$ the box $\mathrm{B}_{\mathrm{k}}$ contains k red balls and $(k+1)$ white balls. Let $P\left(B_1\right)=\frac{1}{2}, P\left(B_2\right)=\frac{1}{3}$ and $\mathrm{P}\left(\mathrm{B}_3\right)=\frac{1}{6} . \mathrm{A}$ box is selected at random and a ball is drawn from it. If a red ball is drawn from it, then the probability that it comes from box $\mathrm{B}_2$ is

A random variable $X$ takes the values $0,1,2,3$, $\qquad$ with probability

$\mathrm{P}(\mathrm{X}=x)=\mathrm{k}(x+1)\left(\frac{1}{5}\right)^x$, where k is a constant.

Then $\mathrm{P}(\mathrm{X}=0)$ is

If $u=\frac{\tan ^{-1} x}{\tan ^{-1} x+1}$ and $v=\tan ^{-1}\left(\tan ^{-1} x\right)$ then $\frac{d u}{d v}=$

If $\bar{a}=\frac{1}{\sqrt{10}}(3 \hat{i}+\hat{k})$ and $\bar{b}=\frac{1}{7}(2 \hat{i}+3 \hat{j}-6 \hat{k})$ then the value of $(2 \overline{\mathrm{a}}-\overline{\mathrm{b}}) \cdot[(\overline{\mathrm{a}} \times \overline{\mathrm{b}}) \times(\overline{\mathrm{a}}+2 \overline{\mathrm{~b}})]=$

If the line $\frac{x+1}{3}=\frac{y-k}{7}=\frac{z-4}{8}$ lies in the plane $2 x+\mathrm{p} y+7 z-41=0$ which is perpendicular to the plane $x+4 y-2 z+13=0$ then $\mathrm{k}=$

The equations of two ellipses are $\frac{x^2}{4}+\frac{y^2}{2}=1$ and $\frac{x^2}{36}+\frac{y^2}{\mathrm{~b}^2}=1$. If the product of their eccentricities is $\frac{\sqrt{2}}{3}$, then the product of the length of the major axis and minor axis of the second ellipse is

A fair coin is tossed 99 times. If X is the number of times head occur then $\mathrm{P}[\mathrm{X}=\mathrm{r}]$ is maximum when $\mathrm{r}=$

The reading of the ammeter in the following circuit is

A wheel initially at rest, begins to rotate about its axis with constant angular acceleration. If it rotates through an angle $\theta_1$ in first 2 s and a further angle $\theta_2$ in the next 2 s , the ratio $\theta_1: \theta_2$ is

The density of a cube is measured by measuring its mass and length of its sides. The \% error in the measurement of mass and length are $5 \%$ and $6 \%$ respectively. The percentage error in the measurement of density is

A mass attached to a spring performs S.H.M. whose displacement is $\mathrm{x}=3 \times 10^{-3} \cos 2 \pi \mathrm{t}$ metre. The time taken to obtain maximum speed for the first time is

If a gas is compressed isothermally then the r.m.s. velocity of its molecules

Three vectors are expressed as $\vec{a}=4 \hat{i}-\hat{j}, \vec{b}=-3 \hat{i}+2 \hat{j}$ and $\vec{c}=-\hat{k}$. The unit vector along the direction of sum of these vectors is

Four polaroids are placed such that the optic axis of each is inclined at an angle of $30^{\circ}$ the optic axis of the preceding one. If unpolarised light of intensity ' $\mathrm{I}_0$ ' falls on the first polaroid, the intensity of light transmitted from the fourth polaroid is $\left[\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$

Two bodies A and B move in same straight line starting from same position. Body moves with constant velocity ' u ' and body B moves with constant acceleration ' $a$ '. When their velocities become equal, the distance between them is

The ratio of angular momentum of an electron in $\mathrm{n}^{\text {th }}$ orbit of hydrogen atom to the velocity of electron in $\mathrm{n}^{\text {th }}$ orbit is proportional to

An element $\overrightarrow{\Delta l}=\Delta \mathrm{xi}$ is placed at the origin and carries a current of 10 A . The magnitude of magnetic field on the Y axis at a distance of 0.5 m if $\Delta x=1 \mathrm{~cm}$ is $\left(\frac{\mu_0}{4 \pi}=10^{-7}\right.$ SI unit $)\left(\sin 90^{\circ}=1\right)$

In an n-p-n transistor amplifier, the collector current is 9 mA . If $90 \%$ of the electrons emitted reach the collector, then

The closed and open organ pipe have same length and when they are vibrating simultaneously in first overtone produce 3 beats. The length of open pipe is made $\left(\frac{1}{3}\right)^{\mathrm{rd}}$ and that of closed pipe is made 3 times the original, the number of beats produced will be (Neglect end correction)

An a.c. e.m.f. of peak value $=230 \mathrm{~V}$ and frequency 50 Hz is connected to a circuit with $\mathrm{R}=11.5 \Omega, \mathrm{~L}=2.5 \mathrm{H}$ and a capacitor all in series. The value of capacitance is ' C ' for the current in the circuit to be maximum. The value of C and maximum current are respectively $\left(\pi^2=10\right)$.

The time period of a satellite of earth is 24 hours. If the separation between the earth and the satellite is decreased to one fourth of the previous value then its new time period will become

A simple pendulum with bob of mass m and conducting wire of length $L$ swings under gravity through an angle $\theta$. The component of earth's magnetic field in the direction perpendicular to swing is B . Maximum e.m.f. induced across the pendulum is ( $\mathrm{g}=$ acceleration due to gravity)

In a cyclic process, work done by the system is

A metal sphere cools at a rate of $1.5^{\circ} \mathrm{C} / \mathrm{min}$ when its temperature is $80^{\circ} \mathrm{C}$. When the temperature of the sphere is $40^{\circ} \mathrm{C}$, its rate of cooling is $0.3^{\circ} \mathrm{C} / \mathrm{min}$. The temperature of the surrounding $\left(\theta_0\right)$ is

The resultant logic gate from the combination of following gates is

A force acting on a body of mass 5 Kg is $(4 \hat{i}-2 \hat{j}+3 \hat{k}) \mathrm{N}$. If the body is initially at rest then the magnitude of its velocity at the end of 10 second in $\mathrm{m} / \mathrm{s}$ will be

The length of closed and open pipe is same. The ratio of frequency of $\mathrm{n}^{\text {th }}$ overtone for closed pipe to that of open pipe is (Neglect end correction)

An e.m.f. $e=E_0 \cos \omega t$ is applied to a circuit containing $L, C$ and $R$ in series where $X_L=3 R$ and $\mathrm{X}_{\mathrm{C}}=\mathrm{R}$. The average power dissipated in the circuit is

The temperature of an air bubble while rising from bottom to surface of a lake remains constant but diameter is doubled. If pressure on the surface is $h$ meter of mercury column and relative density of mercury is ' $\rho$ ' then the depth of the lake is

The apparent wavelength of light from a star moving away from the earth is $0.02 \%$ more than the actual wavelength. The velocity of star is $\left[\mathrm{c}=\right.$ velocity of light $\left.=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right]$

A parallel plate air capacitor has capacitance $C_P$. It is equally filled with parallel layers of materials of dielectric constants $\mathrm{K}_1$ and $\mathrm{K}_2$. Now its capacity becomes $C_K$. The ratio $C_P$ to $C_K$ is

The change in the internal energy of the mass of gas, when the volume changes from V to 2 V at constant pressure P is $\left(\gamma=\frac{\mathrm{Cp}}{\mathrm{Cv}}\right)$

If the length of the potentiometer wire is increased by keeping constant potential difference across the wire, then

A solid sphere rolling without friction on a horizontal surface with a constant speed of $2 \mathrm{~m} / \mathrm{s}$, rolls up on an inclined ramp which is inclined at $30^{\circ}$. The maximum distance travelled by the sphere on the inclined ramp is (acceleration due to gravity $\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2, \sin 30^{\circ}=\frac{1}{2}$ )

In Young's double slit experiment with monochromatic light of wavelength 600 nm , the distance between the slits is $10^{-3} \mathrm{~m}$. For changing the fringe width by $3 \times 10^{-5} \mathrm{~m}$

a. the screen is moved away from the slit by 5 cm .

b. the screen is moved 5 cm towards the slits.

c. the screen is moved 3 cm towards the slits.

d. the screen is moved away from the slits by 3 cm .

An achromatic convergent doublet of two lenses in contact has a power +2 D . The convex lens has power +5 D . The ratio of the dispersive powers of the convergent and divergent lenses is (in magnitude)

Two bar magnets A and B are geometrically similar but the magnetic moment of $A$ is twice that of $B$. $T_1$ is the time period of oscillation when their like poles are kept together. When unlike poles are kept together, the time period of oscillation is $T_2$. The ratio $T_1: T_2$ will be

An ideal transformer converts 220 a.c. to 3.3 kV a.c. to transmit a power of 4.4 kW . If primary coil has 600 turns then alternating current in secondary coil is

Only $4 \%$ of the total current in the circuit passes through a galvanometer. If the resistance of the galvanometer is G , then the shunt resistance connected to the galvanometer is

In hydrogen atom spectrum, when an electron jumps from second excited state to the first excited state, the wavelength of radiation emitted is ' $\lambda$ '. If the electron jumps from the third excited state to the second orbit, the wavelength of radiation emitted will be $\frac{20 \lambda}{x}$. The value of $x$ is

A mass $x$ gram is suspended from a light spring. It is pulled in downward direction and released so that mass performs S.H.M. of period T. If mass is increased by Y gram, the period becomes $\frac{4 \mathrm{~T}}{3}$. The ratio of $\mathrm{Y} / \mathrm{x}$ is

Three inductances are connected as shown in the figure. The equivalent inductance between A and b is

A disc of mass ' $m$ ' and radius ' $r$ ' rolls down an inclined plane of height ' $h$ '. When it reaches the bottom of the plane, its rotational kinetic energy is ( $\mathrm{g}=$ acceleration due to gravity)

The frequency of a stretched uniform wire of length $L$ under tension is in resonance with the fundamental frequency of a closed pipe of same length. If the tension in the wire is increased by 8 N , it is in resonance with the first overtone of the same closed pipe. The initial tension in the wire is

In the following circuit shown in figure, three diodes are connected each with forward resistance $40 \Omega$ and infinite backward resistance. The current through $100 \Omega$ resistance is

Three concentric charged metallic spherical sheets $A, B$ and $C$ have radii $a, b, c$ potentials $V_A$, $\mathrm{V}_{\mathrm{B}}, \mathrm{V}_{\mathrm{C}}$ and charge densities $+\sigma,-\sigma$ and $+\sigma$ respectively. The value of potential $\mathrm{V}_{\mathrm{A}}$ is ( $\varepsilon_0=$ permittivity of free space)

On a photosensitive material, when frequency of incident radiation is increased by $20 \%$, maximum kinetic energy of emitted photoelectrons increases from 0.4 eV to 0.7 eV . The work function of the material is

A parallel plate capacitor with plate area A and plate separation $d$ is charged by constant current $I$. A plane surface of area $\frac{\mathrm{A}}{2}$, parallel to the plates is drawn simultaneously between the plates. The displacement current through this area is

A liquid drop having surface energy $E$ is sprayed into 512 droplets of same size. The final surface energy is

A ray of light of intensity ' I ' is incident on a parallel glass slab at a point ' $A$ ' as shown in figure. It undergoes partial reflection and refraction. At each reflection $25 \%$ of incident energy is reflected. The rays $A B$ and $A B$ undergo interference. The ratio $\frac{\mathrm{I}_{\text {max }}}{\mathrm{I}_{\text {min }}}$ is

A current ' I ' is flowing in a conductor PQRST as shown in figure. The radius of curved path QRS is ' R ' and length of straight portion PQ and ST is very large. The magnetic field at the centre $[\mathrm{O}]$ of the curved part is ( $\mu_0=$ permeability of free space)

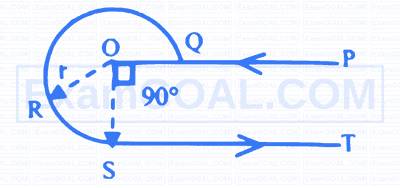
A light of wavelength $\lambda$ is incident on a photosensitive surface of negligible work function. The photoelectrons emitted from the surface have de-Broglie wavelength $\lambda_1$. Then ratio $\lambda: \lambda_1{ }^2$ is

( $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ velocity of light, $\mathrm{m}=$ mass of electron)

Pure water rises through a height $h$ in a capillary tube of internal radius r . Surface tension of water is T . The pressure difference between the water level in the container and the lowest point of the concave meniscus is